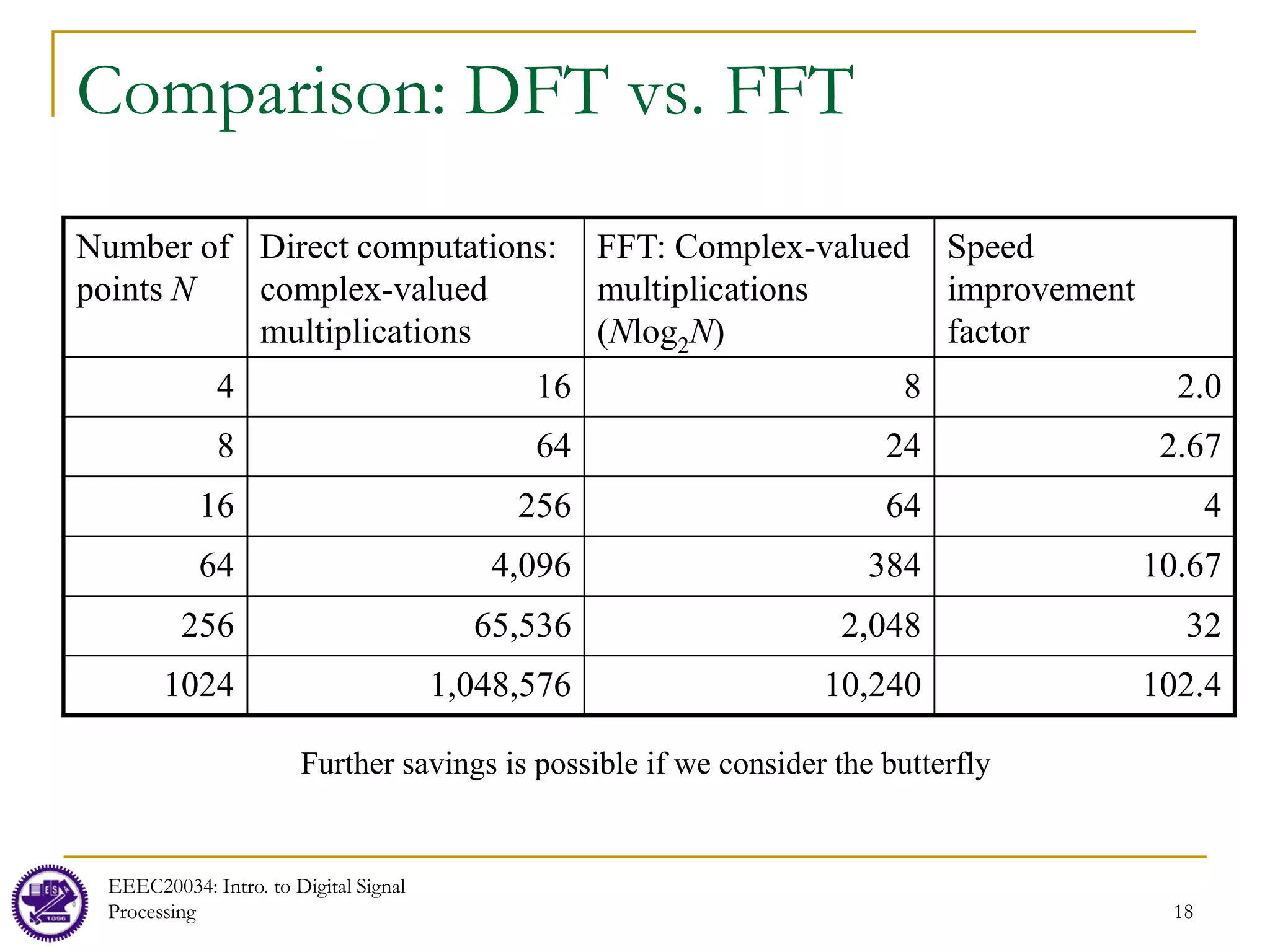
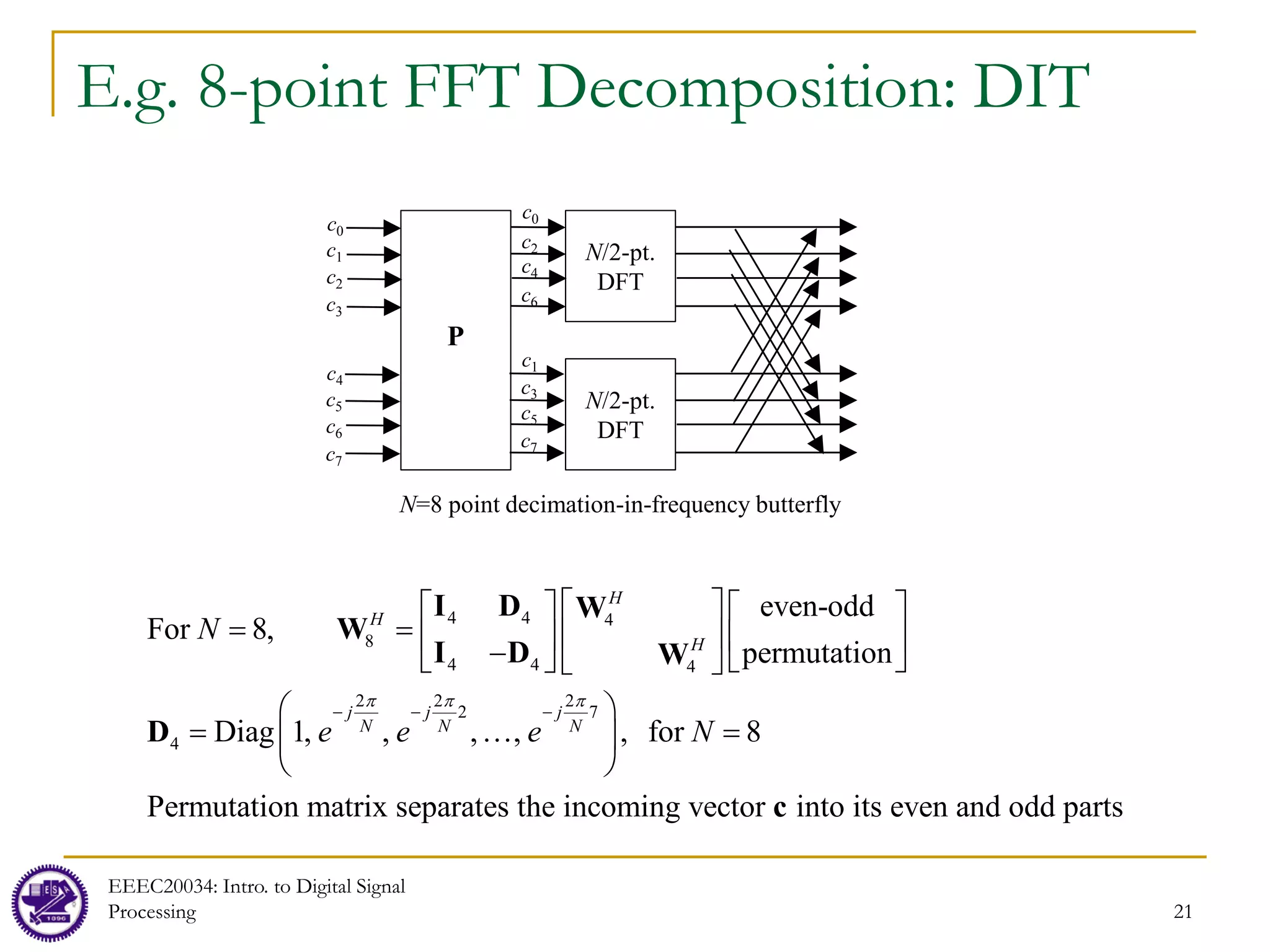
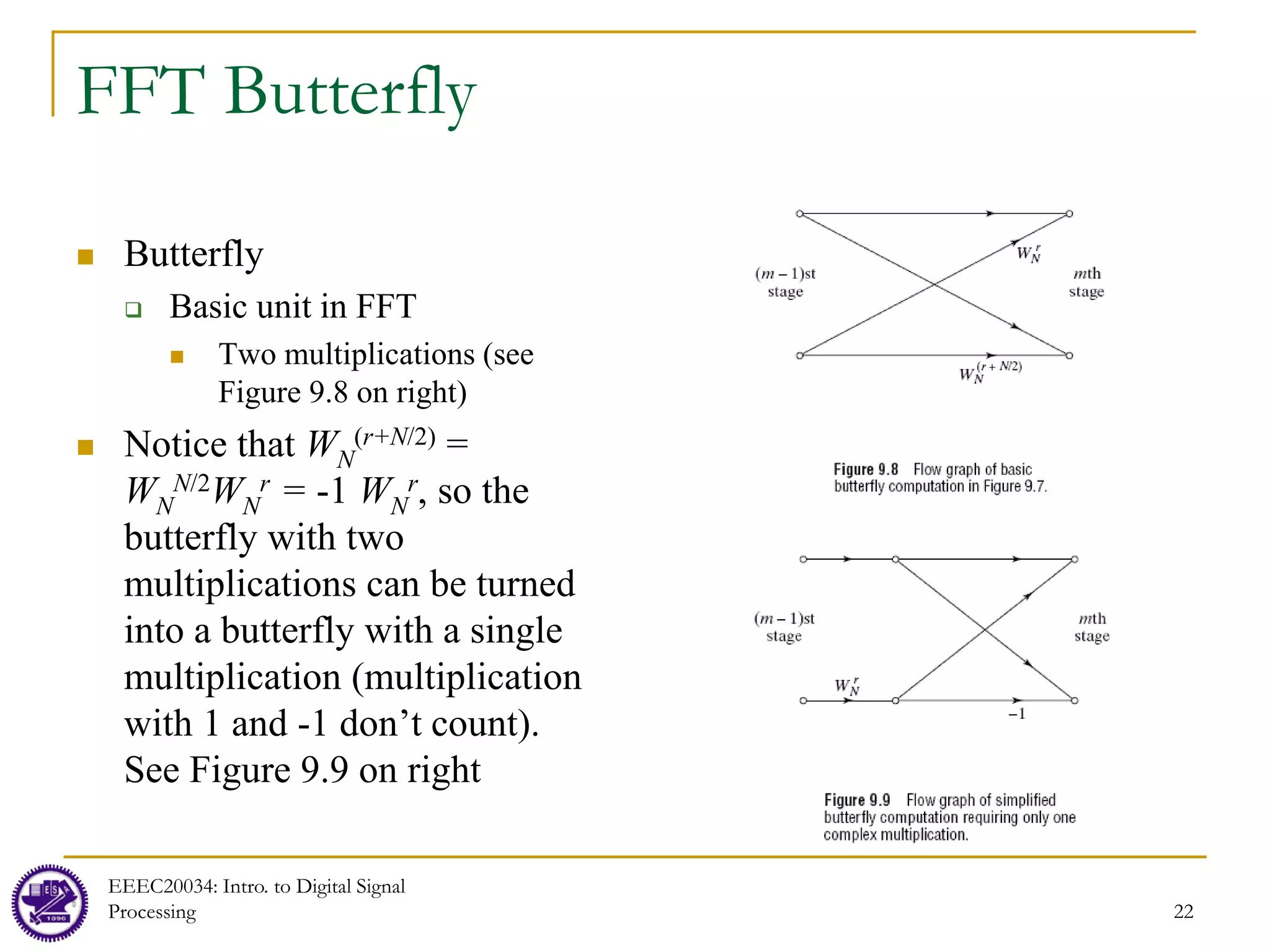
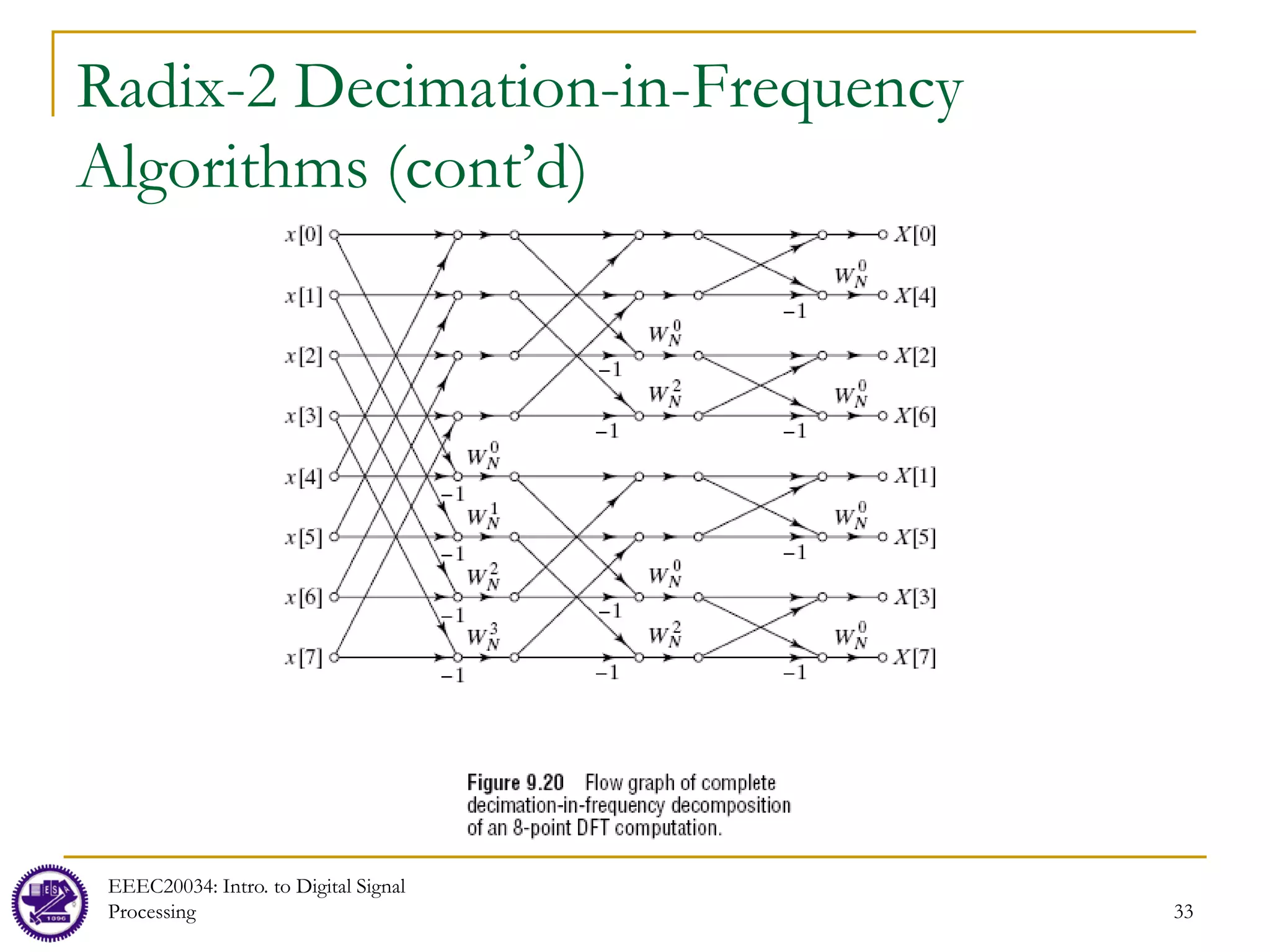
The document discusses computation of the discrete Fourier transform (DFT) and efficient algorithms for computing the DFT, specifically the fast Fourier transform (FFT). It provides an overview of FFTs and notes they are based on a divide and conquer principle. The DFT is described as a linear transformation that can be represented by matrices. Efficient FFT algorithms like the radix-2 algorithm are then presented, showing how an N-point DFT can be broken down into smaller DFTs like N/2-point and N/4-point DFTs, reducing the computational complexity from O(N^2) to O(NlogN).

1. Computation of the DFT
Carrson C. Fung
Institute of Electronics
National Yang Ming Chiao Tung University

2. 2
EEEC20034: Intro. to Digital Signal
Processing 2
Overview
 Efficient algorithms for computing the DFT
 Fast Fourier transform (FFT)
 Many types of FFTs
 Radix-2 (DIT, DIF), Composite N (Cooley-Tukey), Winograd,
Chirp transform, …
 Principle lies in divide and conquer
 Efficient criteria
 Number of multiplications
 Number of additions
 Chip area in VLSI implementation

3. 3
DFT as a Linear Transformation
 Recall that the DFT can be regarded as linear transformation
 Can be computed using matrices
 DFT:
 Let
and
EEEC20034: Intro. to Digital Signal
Processing 3
[ ] [ ]
[ ] [ ]
1
0
1
0
, 0,1, , 1
1
, 0,1, , 1
N
kn
N
n
N
kn
N
k
k n
n
X x W k N
x X W n N
N
k
−
=
−
−
=
= = −
= = −
∑
∑


,
)
1
(
)
1
(
)
0
(
,
)
1
(
)
1
(
)
0
(












−
=












−
=
N
X
X
X
N
x
x
x
N
N


X
x
( )
1
2
2 4 2( 1)
( 1) 2( 1) ( 1)( 1)
1 1 1 1
1
IDFT matrix: , for , 0,1
1
1
1
, 1
N
N N N
nk N
N N N N
N N N N
N N N
W W W
k n N
W W W
W W
N
W
−
−
− − − −
 
 
 
 
= = −
 
 
 
 
W




    


4. 4
DFT as a Linear Transformation
(cont’d)
 Note that for the matrix notation, I split 1/N in the
synthesis equation to both the IDFT and DFT matrix
 Because the matrix (transformation) WN has a
specific structure and because WN
k has particular
values (for some k and n), we can reduce the number
of arithmetic operations for computing this transform
EEEC20034: Intro. to Digital Signal
Processing 4
2
-point DFT
-point IDFT ( is an unitary matrix)
where , ,
1
,
0,1, 1
N N
N N
H
N
j kn
N
nk
N N
N e N
N
N
N
n k
π
 
=
=
=
= … −
 
X W x
x W X W
W

5. 5
Example
 Let
 Compute the 4-point DFT
 DFT matrix
 Thus
 Note that to compute each X[k] value, assuming x[n] is complex-valued, it
requires us to perform N complex-valued multiplications and N-1 complex-
valued additions. To compute all N values of the FFT, it requires N2
complex-valued multiplications and N(N-1) additions
EEEC20034: Intro. to Digital Signal
Processing 5
[ ]
0 1 2 3
T
=
x
0 0 0 0
4 4 4 4
0 1 2 3
4 4 4 4
0 2 4 6
0 2
4 4 4 4
4 4
0 3 6 9
2 2 2
1 2 3
4 4 4
2 2 2
4 2 4 6
4 4 4
2 2 2
3 6 9
4 4 4
4 4 4 4
3 2 1
4 4 4
1 1 1 1
1 1 1 1
1 1 1
1 2
1
1 1 1
2 2
j j j
H
j j j
j j j
W W W W
e e e j
W W W W
W W W W e e W e W
W W W W
e W e W e W
π π π
π π π
π π π
− ⋅ − ⋅ − ⋅
− ⋅ − ⋅ − ⋅
− ⋅ − ⋅ − ⋅
 
 
 
 
 
− −
 
 
= = =
 
 
= =
 
 
 
 
 
 
= = =
 
W
1 1 1 1
1 1
j
j j
 
 
 
 
− −
 
− −
 
4 4
4
3
1
1
1
H j
j
 
 
− +
 
= =
 
−
 
− −
 
X W x

6. 6
Fast Fourier Transform
 Highly efficient algorithms for computing DFT
 General principle: Divide and conquer
 Exploit specific properties of WN
k
 Complex conjugate symmetry: WN
kn = (WN
kn)*
 Symmetry: WN
k+N/2 = -WN
k
 Periodicity: WN
k+N = WN
k
 Particular values of k and n: e.g.radix-4 FFT (no
multiplications: e.g. multiplication by 1 and -1)
EEEC20034: Intro. to Digital Signal
Processing 6

7. 7
FFT
 Direct computation of DFT
 For 1 complex multiplication: x[n]WN
kn requires
 4 real-valued multiplications, 2 real-valued additions
 For each complex-valued addition
 2 real-valued additions
 So, for each k, since we need N complex multiplications and N-1 complex additions
 N complex-valued multiplications = 4N real-valued multiplications and 2N real-valued
additions
 N-1 complex-valued additions = 2(N-1) real-valued additions
 Therefore, 4N real-valued multiplications and 2N+2(N-1) = 4N-2 real-valued additions
 Therefore, to compute all N values of the DFT, we need 4N2 real-valued
multiplications and N(4N-2) real-valued additions.
EEEC20034: Intro. to Digital Signal
Processing 7
( ) ( ) ( ) ( )
[ ]
( ) ( ) ( ) ( )
[ ]
∑
∑
−
=
−
=






+
⋅
+
⋅
−
⋅
=
−
=
⋅
=
1
0
1
0
Re
]
[
Im
Im
]
[
Re
Im
]
[
Im
Re
]
[
Re
1
,
,
1
,
0
,
]
[
]
[
N
n
kn
N
kn
N
kn
N
kn
N
N
n
kn
N
W
n
x
W
n
x
j
W
n
x
W
n
x
N
k
W
n
x
k
X 

8. 8
Radix-2: Decimation-in-Time
Algorithms
 Idea: N-point DFT  N/2-point DFT  N/4-point DFT
N/4-point DFT
 N/2-point DFT  N/4-point DFT
N/4-point DFT
 Sequence: x[0] x[1] x[2] x[3] … x[n/2] … x[N-1]
 Even index: x[0] x[2] … x[N-2]
 Odd index: x[1] x[3] … x[N-1]
EEEC20034: Intro. to Digital Signal
Processing 8

9. 9
Radix-2: Decimation-in-Time
Algorithms (cont’d)
EEEC20034: Intro. to Digital Signal
Processing 9
1
0
even odd
2 2 1
1 1
2 2
2 (2 1)
0 0
2
2 2
2 /2
/2
[ ] [ ] , 0,1, , 1
[ ] [ ]
[2 ] [2 1]
Since
N
kn
N
n
kn kn
N N
n n
n r n r
N N
rk r k
N N
r r
j j
N N
N N
X k x n W k N
x n W x n W
x r W x r W
W e e W
π π
−
=
= = +
− −
+
= =
   
− −
   
   
= = −
= +
= + +
= = =
∑
∑ ∑
∑ ∑




 
]
[
]
[
]
1
2
[
]
2
[
]
[
point DFT
-
2
1
2
0
2
/
point DFT
-
2
1
2
0
2
/
k
H
W
k
G
W
r
x
W
W
r
x
k
X
k
N
N
N
r
rk
N
k
N
N
N
r
rk
N
+
=
+
+
= ∑
∑
−
=
−
= 

 


 


 

 


10. 10
Radix-2: Decimation-in-Time Algorithms
(cont’d)
 Note that G[k] and H[k] are periodic in k with a
period of N/2. Therefore for N = 8
 Similar relationship can be exploited to obtain
X[5], X[6], and X[7]
EEEC20034: Intro. to Digital Signal
Processing 10
[ ] [ ] [ ]
[ ] [ ]
4
4
4
4
4 4 4
0 0
X G W H
G W H
= +
= +

11. 11
Comparison
 Direct computation of N-point DFT (N frequency samples)
 N2 complex-valued multiplications and ~N2 (it’s actually N(N-1), but we shall assume N is large)
complex-valued additions
 Direct computation of N/2-point DFT
 We need to perform 2(N/2)-point DFTs, each one will require (N/2)2 complex-valued
multiplications and approximately (N/2)2 complex-valued additions. Therefore, we need to
perform 2(N/2)2 complex-valued multiplications and 2(N/2)2 complex-valued additions
 Combining the 2(N/2)-point DFTs also requires
 an additional N complex-valued multiplications (because we need to multiply the WN
k terms)
 an additional N complex-valued additions (combining the G[k] and H[k] terms)
 Adding everything together, we have:
 N + 2(N/2)2 = N + N2/2 complex-valued multiplications
 N + 2(N/2)2 = N + N2/2 complex-valued additions
 For N>2, N+N2/2 < N2, therefore, this divide-and-conquer approach does decrease the amount of
computations
 log2N-stage FFT
 Since N=2v, we can further break N/2-point DFT into two N/4-point DFT and so on
EEEC20034: Intro. to Digital Signal
Processing 11

12. 12
(N/4)-point DFT: G[k]
EEEC20034: Intro. to Digital Signal
Processing 12
[ ] [ ]
[ ] [ ] ( )
[ ] [ ]
/2 1
/2
0
/4 1 /4 1
2 1
2
/2 /2
0 0
/4 1 /4 1
/4 /2 /4
0 0
2 2 1
2 2 1
N
rk
N
r
N N
k
k
N N
N N
k k k
N N N
G k g r W
g W g W
g W W g W
−
=
− −
+
= =
− −
=
=
= + +
= + +
∑
∑ ∑
∑ ∑


 
 
 
 
 

13. 13
(N/4)-point DFT: H[k]
EEEC20034: Intro. to Digital Signal
Processing 13
[ ] [ ]
[ ] [ ] ( )
[ ] [ ]
/2 1
/2
0
/4 1 /4 1
2 1
2
/2 /2
0 0
/4 1 /4 1
/4 /2 /4
0 0
2 2 1
2 2 1
N
rk
N
r
N N
k
k
N N
N N
k k k
N N N
H k h r W
h W h W
h W W h W
−
=
− −
+
= =
− −
=
=
= + +
= + +
∑
∑ ∑
∑ ∑


 
 
 
 
 
N/4-point
DFT
N/4-point
DFT
x[1]
x[5]
x[3]
x[7]
WN/2
0
WN/2
1
WN/2
2
WN/2
3
H[0]
H[1]
H[2]
H[3]

14. 14
Combining G[k] and H[k]
 Combining the two
figures above and
realizing that WN/2
k =
WN
2k, we can obtain
Figure 9.5
EEEC20034: Intro. to Digital Signal
Processing 14

15. 15
2-point DFT
 Assuming N = 8, the
(N/4)-point DFT is
actually a 2-point DFT
EEEC20034: Intro. to Digital Signal
Processing 15

16. 16
8-point DIT
 Then substituting the 2-
point DFT structure in
Figure 9.6 into Figure
9.5, we have the
structure in Figure 9.7
EEEC20034: Intro. to Digital Signal
Processing 16

17. 17
Number of Operations
 For a general N-point DFT, and assuming N is still a power of 2, we can decompose
any N-point DFT into 2 (N/2)-point DFT, then the 2 (N/2)-point DFTs can be
further decomposed into 4 (N/4)-point DFTs, then the 4 (N/4)-point DFTs can be
decomposed into 8 (N/8)-point DFTs, and so on until we are left with a 2-point
DFT
 There are a total of v = log2 N number of stages of computations
 Following the same logic as before for the N-point DFT, where we can decompose
it into 2 (N/2)-point DFT, which requires N + 2(N/2)2 complex-valued
multiplications and N + 2(N/2)2 complex-valued additions. Decomposing the (N/2)-
point DFT into (N/4)-point DFT requires us to replace the (N/2)2 term into N/2 +
2(N/4)2. Therefore, we need to perform N+2(N/2 + 2(N/4)2) = N + N + 4(N/4)2
complex-valued multiplications and N+2(N/2 + 2(N/4)2) = N + N + 4(N/4)2
complex-valued additions
 This can be done at most v times, so the number of complex-valued multiplications
and additions is equal to Nv = Nlog2 N
EEEC20034: Intro. to Digital Signal
Processing 17

18. 18
Comparison: DFT vs. FFT
Number of
points N
Direct computations:
complex-valued
multiplications
FFT: Complex-valued
multiplications
(Nlog2N)
Speed
improvement
factor
4 16 8 2.0
8 64 24 2.67
16 256 64 4
64 4,096 384 10.67
256 65,536 2,048 32
1024 1,048,576 10,240 102.4
Further savings is possible if we consider the butterfly
EEEC20034: Intro. to Digital Signal
Processing

19. FFT in Matrix Form: 4-point FFT
EEEC20034: Intro. to Digital Signal
Processing 19
2
4
Consider the 4-point DFT matrix and consider decimation-in-time in which the inputs are
permuted (bit
1 1 1 1 1 1 1 1
1 1 1
1 1 1 1 1 1
1 1
-reversed) becomes
1
1 1
1
1
H j j
j j
j
j j
   
   
−
   
= =
   
− − −
   
− −
   
− −
W
2
1
1
1
1
j
   
   
   
   
   
   
Even-odd
permutation
x[0]
x[2]
x[1]
x[3]
X[0]
X[1]
X[2]
X[3]
1
4
W j
= −
0
4 1
W =
2
4 1
W = −
3
4
W j
=
x[0]
x[1]
x[2]
x[3]
0
2 1
W =
1
2 1
W = −
2
2 1
W =
3
2 1
W = −

20. General 1024-point FFT Decomposition
EEEC20034: Intro. to Digital Signal
Processing 20
512 512 512
1024
512 512 512
2 2 2
2 511
512
2
512
even-odd
1024,
permutation
Diag 1, , , ,
FFT Decompo
, for 1024.
, 0
sition
For
, fo ,
r ,
2
H
H
H
j j j
N N N
j kn
H N
kn
N
e e e N
N
e n k
π π π
π
− − −
−
 
   
=  
   
−  
   
 
… =
 
 
  …

=
= =

I D W
W
I D W
D
W 1
−

21. E.g. 8-point FFT Decomposition: DIT
EEEC20034: Intro. to Digital Signal
Processing 21
4 4
8
4 4
2 2 2
2
4
7
4
4
even-odd
8,
permutation
Diag 1, , , ,
F
, for 8
Permutation matrix separates the incoming vector into its even and odd part
or
s
H
H
H
j j j
N N N
N
e e e N
π π π
− − −
 
   
= =  
   
−  
   
 
… =
 
 
=
I D W
W
I D W
D
c
N/2-pt.
DFT
N/2-pt.
DFT
P
N=8 point decimation-in-frequency butterfly
c0
c1
c2
c3
c4
c5
c6
c7
c2
c4
c6
c1
c3
c5
c7
c0

22. 22
FFT Butterfly
 Butterfly
 Basic unit in FFT
 Two multiplications (see
Figure 9.8 on right)
 Notice that WN
(r+N/2) =
WN
N/2WN
r = -1 WN
r, so the
butterfly with two
multiplications can be turned
into a butterfly with a single
multiplication (multiplication
with 1 and -1 don’t count).
See Figure 9.9 on right
EEEC20034: Intro. to Digital Signal
Processing

23. 23
8-point DIT Using Simplified Butterfly
Structure
Now we have an additional savings by a factor of 2 since at every
butterfly, we have halved the number of multiplications!
EEEC20034: Intro. to Digital Signal
Processing

24. 24
In-Place Computations
 Besides efficient computation of the DFT, the structure in Figure 9.10 also offers an efficient
way to storage the original data and the results of the computations in the intermediate stages
 Each stage of the FFT process has N inputs and N outputs, so we need exactly N storage
locations at any one point in the calculations
 It is possible to reuse the same storage locations at each stage to reduce memory overhead
 Any algorithm which uses the same memory to store successive iterations of a calculation is called an
“in-place” algorithm
 Computation must be done in a specific order
 Let Xm[p] and Xm[q] denote the results from the mth stage of computations and Xm-1[p] and Xm-
1[q] denote the results from the (m-1)th stage of computations. Then the relationship between
the input and output of the butterfly can be written as (see Figure 9.11)
Only two registers are needed for computing a butterfly unit because Xm[p] and Xm[q] are
stored in the same storage registers as Xm-1[p] and Xm-1[q], respectively. This is because once
Xm[p] and Xm[q] are produced from Xm-1[p] and Xm-1[q], there is no need to store Xm-1[p] and
Xm-1[q] anymore, so we can place the new results, Xm[p] and Xm[q], into the storage location of
Xm-1[p] and Xm-1[q]
]
[
]
[
]
[
]
[
]
[
]
[
1
1
1
1
q
X
W
p
X
q
X
q
X
W
p
X
p
X
m
r
N
m
m
m
r
N
m
m
−
−
−
−
−
=
+
=
EEEC20034: Intro. to Digital Signal
Processing

25. 25
In-Place Computations (cont’d)
In order to retain the in-place computation property, the input data are accessed in the bit-reversed
order. This gives us an easy way to index the data
Note: The outputs are in the normal order (same as the “position”)
Position Binary
equivalent
Bit reversed Sequence
index
6 110 011 3
2 010 010 2
Remark: Index 3 input data is placed at position 6
EEEC20034: Intro. to Digital Signal
Processing

26. 26
In-Place Computations (cont’d)
 We may also place the
inputs in the normal order;
then the outputs are in the
bit-reversed order to obtain
the structure in Figure 9.14
EEEC20034: Intro. to Digital Signal
Processing

27. 27
In-Place Computations (cont’d)
 If we try to maintain the
normal order of both inputs
and outputs, then in-place
computation structure is
destroyed. The structure is
shown in Figure 9.15. There is
no advantage in using this
structure since there is no in-
place computation (cannot
save storage space), and no
easy way to index the data (the
input data are not stored in bit-
reversed order)
EEEC20034: Intro. to Digital Signal
Processing

28. 28
Radix-2 Decimation-in-Frequency
Algorithms
Dividing the output sequence X[k] into smaller pieces
[ ] [ ]
1
0
, 0,1, , 1
N
kn
N
n
X k x n W k N
−
=
= = −
∑ 
Assuming N = 2v, where v is an integer. If k is even, i.e. k = 2r, then
1
0
1
1
2
2 2
0
2
1 1
2 2 2
2 2
0 0
2 [ ] 2 2
2
[2 ] [ ] , 0,1, , 1
2
[ ] [ ] ( ) in second term
2
[ ]
2
[ ]
2
N
kn
N
n
N
N
nr nr
N N
N
n n
N N
N
r n
nr
N N
n n
N
r n rn rN rn
N N N N
N
X r x n W r
N
x n W x n W n n
N
x n W x n W
W W W W
N
x n x n
−
=
−
−
= =
− −  
+
 
 
= =
+
= = −
= + ← +
 
= + + ⋅
 
 
= =
  
= + +
 
 

∑
∑ ∑
∑ ∑


1
2
2
0
1
2
2
0
[ ]
2
N
nr
N
n
N
nr
N
n
W
N
x n x n W
−
=
−
=

⋅
 

 
 
= + + ⋅
 
 
 
 
∑
∑
EEEC20034: Intro. to Digital Signal
Processing

29. Radix-2 Decimation-in-Frequency
Algorithms
EEEC20034: Intro. to Digital Signal
Processing 29
[ ] [ ] ( )
[ ] ( )
[ ] ( )
[ ] ( ) ( )
1
2 1
0
1
1
2
2 1 2 1
0
2
1
1 2 2 1
2 1 2
0
2
2 1, 0,1, , 1
2
2 1
Let ,
For
then
2 2
N
n r
N
n
N
N
n r n r
N N
N
n n
N
N
N n r
n r
N N
N n
n
N
k r r
X r x n W
x n W x n W
N N
n n x n W x n W
−
+
=
−
−
+ +
= =
−  
− + +
 
+  
=
=
= + = … −
+ =
= +
 
→ + = +
 
 
∑
∑ ∑
∑ ∑
( ) ( )
1
2
2 1
2 1
2
0 2
N
N
r
n r
N N
n
N
W x n W
−
 
+
  +
 
=
 
= +
 
 
∑

30. Radix-2 Decimation-in-Frequency
Algorithms
EEEC20034: Intro. to Digital Signal
Processing 30
( )
[ ] ( ) ( )
[ ] [ ] ( ) ( )
2 1 2
2 2 2
1
1 2
2 1 2 1
0
2
1
2
2 1 2 1
0 0
Note 1. Therefore
2
So
2 1
2
1
N N N
r r
N N N
N
N
n r n r
N N
N n
n
N
n r n r
N N
n n
W W
N
x n W x n W
N
X r
W
x n W x n W
   
+
   
   
−
−
+ +
=
=
−
+ +
= =
⋅−
 
=
− +
 
 
 
+
= − +

=

 
=
∑ ∑
∑
[ ] ( )
[ ]
1
2
1 1
2 2
2 1
/2
0 0
2 2
N
N N
n r n nr
N N N
n n
N N
x n x n W x n x n W
W
−
− −
+
=
   
   
= − + = − +
   
   
   
   
∑
∑ ∑
[ ] [ ] ( ) ( ) ( )
1 1
2 2
2 1
2 1 2 1
2
0 0
2 1
2
N N
N
r
n r n r
N N N
n n
N
X r x n W W x n W
− −
 
+
 
+ +
 
= =
 
+
= + +
 
 
∑ ∑
2
/2
nr nr
N N
W
W =

31. 31
Radix-2 Decimation-in-Frequency
Algorithms (cont’d)
[ ] [ ]
1
2
0
0
2
1
2
/
2
2 1
[ ] [ ]
2
2
2
N
n nr
N N
n
N
nr
N
n
N
X r x n x n W
W
N
X r x n x n W
−
=
−
=
 
 
+ =

 
 
 = + + ⋅
 
 
− +
 
 
 
 
  
  





∑
∑













+
−
=






+
+
=
2
]
[
]
[
2
]
[
]
[
N
n
x
n
x
n
h
N
n
x
n
x
n
g
EEEC20034: Intro. to Digital Signal
Processing
/2 is refers to
the /2-point DFT
nr
N
N
W

32. 32
Radix-2 Decimation-in-Frequency
Algorithms (cont’d)
 We can further break into
even and odd groups (just like
DIT). Again, we can reduce
the two-multiplication
butterfly into one
multiplication. Hence, the
computational complexity is
about (N/2)log2 N. The in-
place computation property
holds if the outputs are in bit-
reversed order (when inputs
are in the normal order)
EEEC20034: Intro. to Digital Signal
Processing

33. 33
Radix-2 Decimation-in-Frequency
Algorithms (cont’d)
EEEC20034: Intro. to Digital Signal
Processing

34. 34
FFT for Composite N
 When N is not a power of 2, but a product of 2 or more
integers, FFT algorithms still exist to compute the DFT
 If N is a prime number, we can simply pad zeros to make
N into an composite integer
 Cooley-Tukey Algorithm: N = N1N2
 DIT and DIF are special cases of Composite N algorithm
where N = 2(N/2) = (N/2)2
 For composite N FFT, we can divide x[n] and X[k] into a
two-dimensional array
EEEC20034: Intro. to Digital Signal
Processing

35. 35
Example
 For x[n] in this case, n1 is the column index and n2 is the
row index. There will be N2 elements in each column (i.e.
N2 number of rows) of the two-dimensional array which
stores x[n].
 For X[k], k1 is the column index and k2 is the row index.
There will be N1 elements in each row (i.e. N1 number of
columns) of the two-dimensional array which stores X[k]
1 1
1 1 2
2 2
1
2 1 2
1
2 1 2
2 2
1 1 2
0 1
Time index: or
0 1
0 1
Freq. index: or
0 1
n N n n
k k
n N
n n N n
n N
k N
k N k k
k N
N k
 ≤ ≤ −

= + 

≤ ≤ −
 

≤ ≤ −

 = + 
 ≤ ≤ −

= +

= +
EEEC20034: Intro. to Digital Signal
Processing

36. 36
Example (cont’d)
For example: N1 = 2, N2 = N/N1 = N/2, then the input signal x[n] can be arranged
into a 2-dimensional array as
n1
n2
0 1
0 x[0] x[N/2]
1 x[1] x[N/2+1]
.
.
.
.
.
.
N2-1 x[N/2-1] x[N-1]
EEEC20034: Intro. to Digital Signal
Processing

37. 37
Decomposition
Goal: Decompose N-point DFT into two stages: let n = N2n1 + n2 and k=k1 + N1k2
N1-point DFT⊗N2-point DFT
( )( )
2 1
1 1 2 2 1 2
2 1
2 1
2 1 1 1 2 2 1 2 1 2 2 1
2 1 1 1 2 2
1 2
1
1
0
1 1 2
1 1
2 1 2
0 0
1 1
2 1 2
0 0
1
2 1 2
[ ] [ ] , 0 1
[ ]
[ ]
[ ]
[ ]
k n k n
N N
N
kn
N
n
N N
k N k N n n
N
n n
N N
N k n k n k N n N N k n
N N N N
n n
W W
k
N
X k x n W k N
X k N k
x N n n W
x N n n W W W W
x N n n W
−
=
− −
+ +
= =
− −
= =
= ≤ ≤ −
= +
= + ⋅
= + ⋅ ⋅ ⋅ ⋅
= + ⋅
∑
∑ ∑
∑ ∑ 

  




2 1
1 1 1 2 2 2
2
2 1
1
2
1 1
0 0 twiddle
factor
-point
-point
N N
n k n k n
N N
n n
N
N
W W
− −
= =
 
 
 
 
⋅ ⋅
 
 
 
 
 
 
∑ ∑








EEEC20034: Intro. to Digital Signal
Processing

38. 38
Procedure
1
1 1
1
1
1 2
1
1 1
2 1 2 1 2
0 2 2
(1) Compute -point DFT of all rows: (row transform)
0 1
[ , ] [ ] ,
0 1
(2) Each row DFTs are multiplied by twiddle factors:
N
k n
N
n
N N
k N
G n k x N n n W
n N
−
=
≤ ≤ −

= + ⋅ 
≤ ≤ −

∑
1 2
2
2 2
2
2
1 1
2 1 2 1
2 2
2
1
1 1 2 2 1
0
0 1
[ , ] [ , ],
0 1
(3) Compute -point DFT: (column transform)
[ ] [ , ]
k n
N
N
k n
N
n
k N
G n k W G n k
n N
N
X k N k G n k W
−
=
≤ ≤ −

= ⋅ 
≤ ≤ −

+ = ⋅
∑


EEEC20034: Intro. to Digital Signal
Processing

39. 39
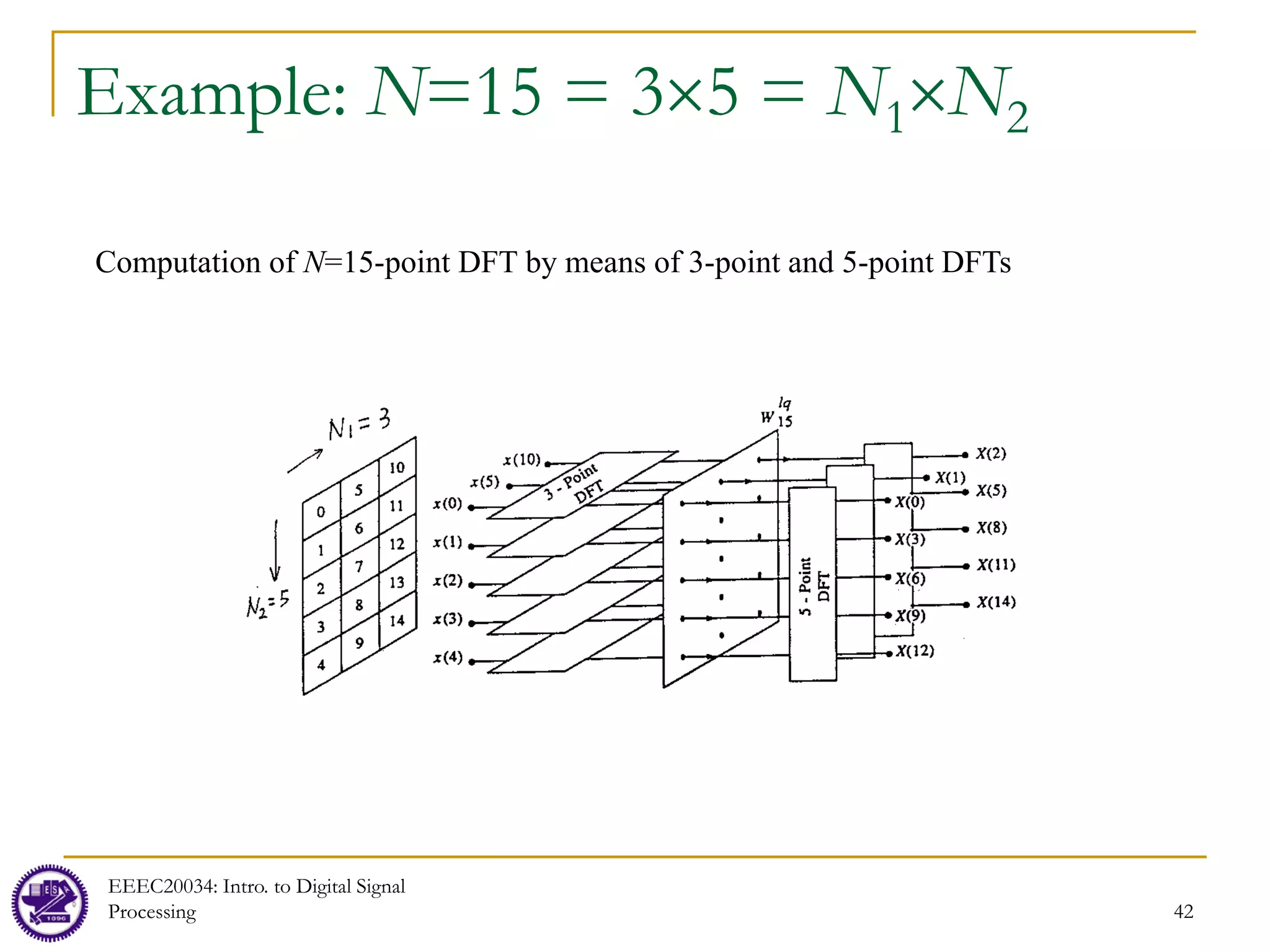
Example: N=15 = 3×5 = N1×N2
Row 1 x[0,0] = x[0] x[0,1] = x[5] x[0,2] = x[10]  G[0,k1]
Row 2 x[1,0] = x[1] x[1,1] = x[6] x[1,2] = x[11]  G[1,k1]
Row 3 x[2,0] = x[2] x[2,1] = x[7] x[2,2] = x[12]  G[2,k1]
Row 4 x[3,0] = x[3] x[3,1] = x[8] x[3,2] = x[13]  G[3,k1]
Row 5 x[4,0] = x[4] x[4,1] = x[9] x[4,2] = x[14]  G[4,k1]
First, perform a 3-point DFT for each of the five rows (Notations: x[n2,n1], G[n2,k1]):
EEEC20034: Intro. to Digital Signal
Processing

40. 40
Example: N=15 = 3×5 = N1×N2
Multiply by 1 2
k n
N
W
Column 1 Column 2 Column 3
[ ]
0,0
G

[ ]
1,0
G

[ ]
2,0
G

[ ]
3,0
G

[ ]
4,0
G

[ ]
0,1
G

[ ]
1,1
G

[ ]
2,1
G

[ ]
3,1
G

[ ]
4,1
G

[ ]
0,2
G

[ ]
1,2
G

[ ]
2,2
G

[ ]
3,2
G

[ ]
4,2
G

EEEC20034: Intro. to Digital Signal
Processing

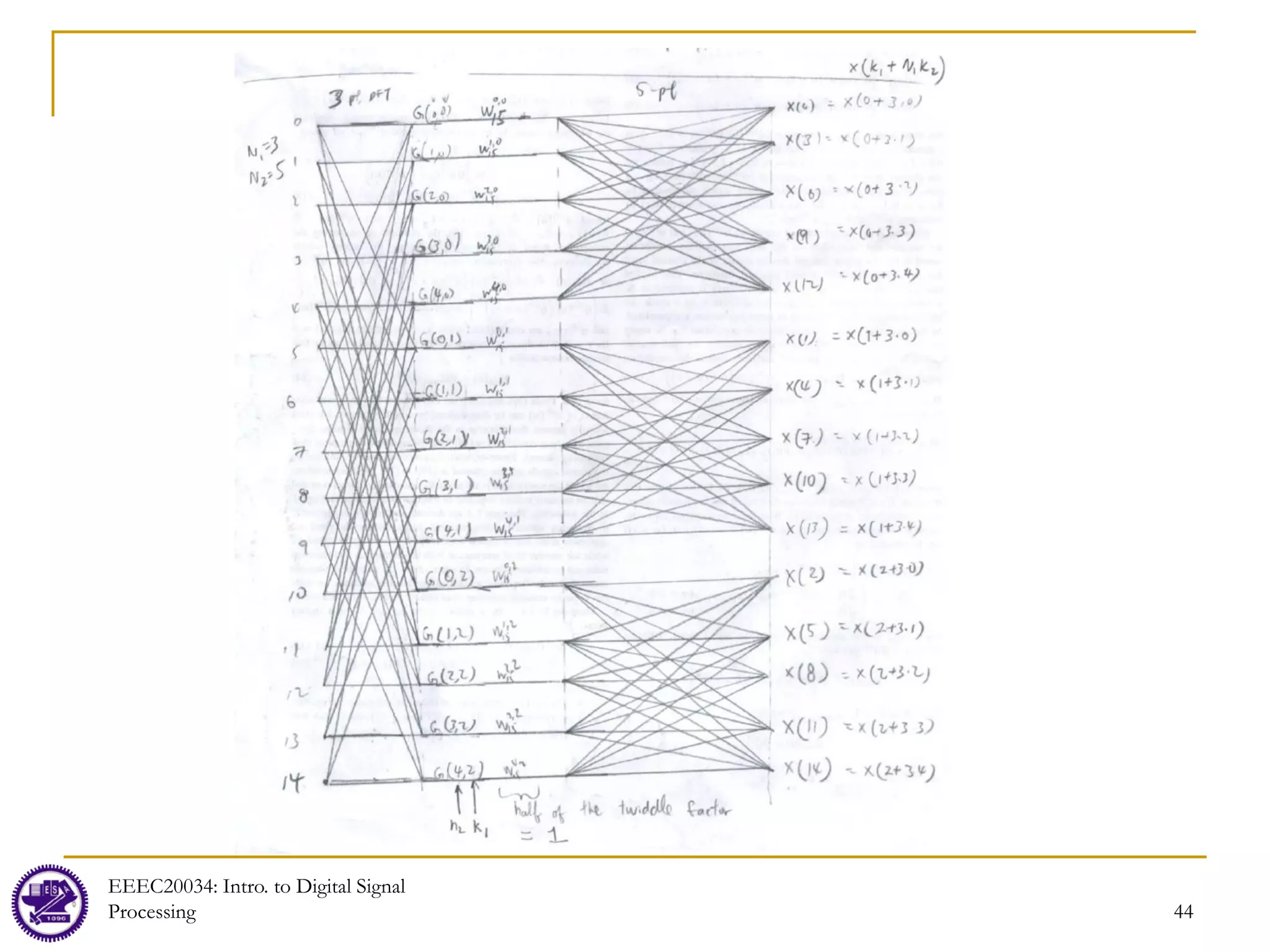
41. 41
Example: N=15 = 3×5 = N1×N2
Compute the 5-point DFT for each of the three columns
X[0,0] = X[0] X[0,1] = X[1] X[0,2] = X[2]
X[1,0] = X[3] X[1,1] = X[4] X[1,2] = X[5]
X[2,0] = X[6] X[2,1] = X[7] X[2,2] = X[8]
X[3,0] = X[9] X[3,1] = X[10] X[3,2] = X[11]
X[4,0] = X[12] X[4,1] = X[13] X[4,2] = X[14]
EEEC20034: Intro. to Digital Signal
Processing

42. 42
Example: N=15 = 3×5 = N1×N2
Computation of N=15-point DFT by means of 3-point and 5-point DFTs
EEEC20034: Intro. to Digital Signal
Processing

43. 43
Example: N=15 = 3×5 = N1×N2 - Butterfly Structure
EEEC20034: Intro. to Digital Signal
Processing

44. 44
EEEC20034: Intro. to Digital Signal
Processing

45. 45
Computational Complexity
 Extension: N = N1N2…Nv
 If N = N1N2
 1. row transform: N2⋅µ(N1)
 2. twiddle factors: N1N2 = N
 3. column transform: N1⋅µ(N2)
 In the example above, when N2 = 5 and N1 = 3. We first have to perform 5 different 3-point DFT
(row transform), so the number of multiplications will be 5 times µ(3), where µ(3) is the number of
multiplications we need to perform for a 3-point DFT. There are 15 twiddle factor multiplications
(counting all trivial multiplications as well). Finally, there are three 5-point DFT to perform in the
last stage, therefore, 3 times µ(5) number of multiplications
 In general if N = N1N2…Nv, then by repeatly applying (*), we have . This is
achieved by continuously breaking down the transform into successively smaller transforms. N(v-1)
accounts for the total number of twiddle factor multiplication. However, it should be N(v-1)/2
because half of the twiddle factors are actually equal to “1” (see example when N = N1N2 = 3*5)
 Note that the way we reduce the number of computations is to obtain efficient algorithms for
implementing the smaller Ni-point transforms with few than Ni
2 multiplications








−
+
= ∑
=
ν
ν
µ
µ
1
)
1
(
)
(
)
(
i i
i
N
N
N
N
2 1 1 2
1 2
1 2
( ) ( ) ( )
(*)
( ) ( )
1
N N N N N N
N N
N
N N
µ µ µ
µ µ
= ⋅ + ⋅ +
 
= + +
 
 
EEEC20034: Intro. to Digital Signal
Processing

46. 46
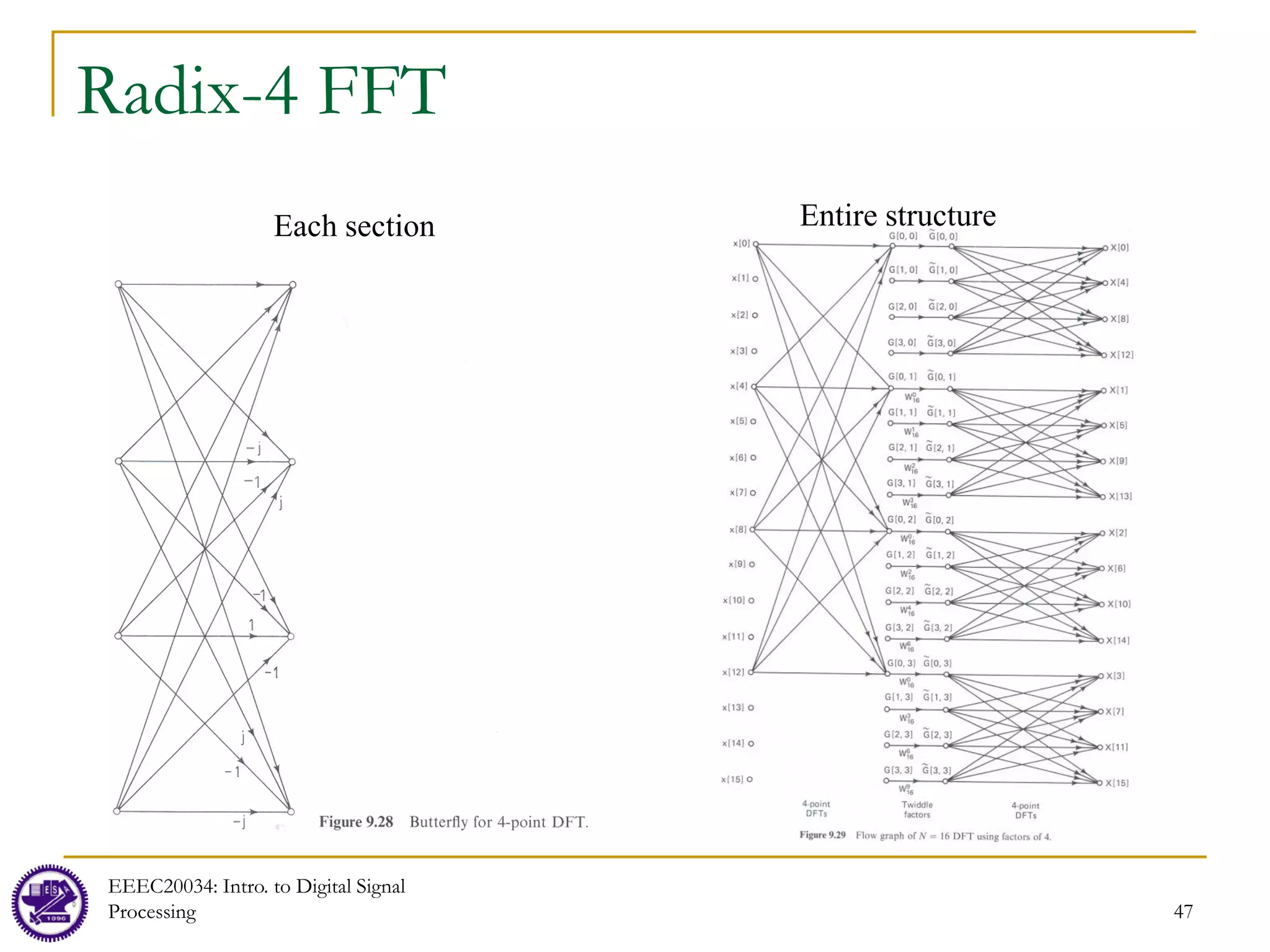
Special Case: N1 = N2 = … = Nv = 2
( )
( )
( )
( )
1 2 2
1 2 4
Radix-2: 2 and log
1
( ) multiplications because 2 requires no multiplications
2
Radix-4: 4 and log
1
( ) multiplications because 4
2
N N N v N
N v
N
N N N v N
N v
N
ν
ν
µ µ
µ µ
= = = = =
−
=
= = = = =
−
=


requires no multiplications
(multiplications by and - can be achieved by interchanging the real and
imaginary parts). This FFT has few stages than Radix-2 fewer mult
j j
⇒
0 0 0 0
4 4 4 4
1 2 3
0 1 2 3
4 4 4
4 4 4 4
4 2 0 2
0 2 4 6
4 4 4
4 4 4 4
3 2 1
0 3 6 9
4 4 4
4 4 4 4
1 2
2
s
1 1 1 1 1 1 1 1
1 1 1
1 1 1 1 1
1 1 1
For example, let 16 4*4
,
W W W W
W W W j j
W W W W
W W W
W W W W
W W W j j
W W W W
N N N
G n k
     
     
− −
     
= = =
     
− −
     
− −
   
 
 
= = =
W
[ ] [ ] ( ) ( ) ( ) ( ) ( ) ( )
1 1 1
1 2 2 2 2
1 2
/ 4 1 / 2 3 / 4 ,
for 0,1,2,3; 0,1, ( / 4) 1
k k k
x n j x N n x N n j x N n
k n N
= + − + + − + + +
     
     
= = −

EEEC20034: Intro. to Digital Signal
Processing

47. 47
Radix-4 FFT
Each section Entire structure
EEEC20034: Intro. to Digital Signal
Processing

48. 48
Implementation of Inverse FFT Using
FFT
( )
[ ]
1
0
1
0
*
1
*
0
1
*
0
*
1
IDFT: [ ] [ ] (*)
DFT: [ ] [ ]
Hence, take the conjugate of (*)
1
[ ] [ ]
1
[ ]
1
DFT
N
kn
N
k
N
nk
N
n
N
kn
N
k
N
kn
N
k
x n X k W
N
X k x n W
x n X k W
N
X k W
N
X k
N
−
−
=
−
=
−
−
=
−
=
= ⋅
= ⋅
 
= ⋅
 
 
= ⋅

= 
∑
∑
∑
∑


[ ]
[ ]
( )
[ ]
( )
*
*
*
*
*
Then take the conjugate of
1
[ ] DFT
1
FFT
Thus, we can use the FFT algorithm
to compute the inverse DFT
x n
x n X k
N
X k
N
 
=  
 
=  
EEEC20034: Intro. to Digital Signal
Processing