This document discusses face recognition and the PCA algorithm for face recognition. It begins with an introduction to face recognition and its uses. It then explains the PCA algorithm for face recognition in 6 steps: 1) converting images to vectors, 2) normalizing the vectors, 3) calculating eigenvectors from the normalized vectors, 4) selecting important eigenvectors, 5) representing faces as combinations of eigenvectors, and 6) recognizing faces. It discusses the strengths and weaknesses of face recognition and lists several applications such as access control, law enforcement, and banking.

1. By Ashwini Awatare

2. Contents:-
 Introduction
 Face Recognition
 Face Recognition using PCA algorithm
 Strengths & Weaknesses
Applications
Conclusion
Resources

3. Introduction
Facial recognition (or face recognition) is a type
of biometric software application that can identify a
specific individual in a digital image by analyzing and
comparing patterns.
Facial recognition systems are commonly used for
security purposes but are increasingly being used in a
variety of other applications. For example,
The Kinect motion gaming system, uses facial
recognition to differentiate among players.

4. WHAT IS FACE RECOGNITION?
“Face Recognition is the task
of identifying an already
detected face as a KNOWN
or UNKNOWN face, and
in more advanced cases
TELLING EXACTLY WHO’S IT IS ! “
FACE DETECTION FEATURE
EXTRACTION
FACE
RECOGNITION

5. All identification or authentication technologies
operate using the following four stages:
 Capture: A physical or behavioral sample is
captured by the system during Enrollment and
also in identification or verification process.
 Extraction: unique data is extracted from the
sample and a template is created.
 Comparison: the template is then compared
with a new sample.
 Match/non-match: the system decides if the
features extracted from the new Samples are a
match or a non match.
10/17/2014 5

6. PCA ALGORITHM
STEP O : Convert image of training set to image
vectors
 A training set consisting of total M images
Each image is of size N x N

7. STEP 1: Convert image of training set to image
vectors
A training set consisting of total M image
Image converted to vector
For each (image in
training set)
N x N Image
N
Ti Vector
Free vector space

8. STEP 2: Normalize the face vectors
1. Calculate the average face vector
 A training set consisting of total M image
Image converted to vector
……
 Free vector space
Calculate average face vector ‘U’
Ti
U

9.  STEP 2: Normalize the face vectors
1. Calculate the average face vectors
2. Subtract avg face vector from each face vector
 A training set consisting of total M image
Image converted to vector
……
 Free vector space
Calculate average face vector ‘U’
Then subtract mean(average)
face vector from EACH face
vector to get to get normalized
face vector
Øi=Ti-U
Ti
U

10. STEP 2: Normalize the face vectors
1. Calculate the average face vectors
2. Subtract avg face vector from each face vector
 A training set consisting of total M image
Image converted to vector
……
 Free vector space
Øi=Ti-U
Eg. a1 – m1
a2 – m2
Ø1= . .
. .
a3 – m3
Ti
U

11. STEP 3: Calculate the Eigenvectors (Eigenvectors
represent the variations in the faces )
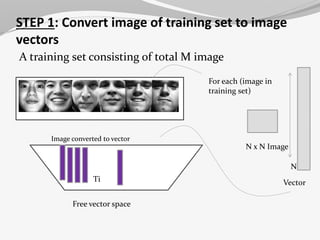
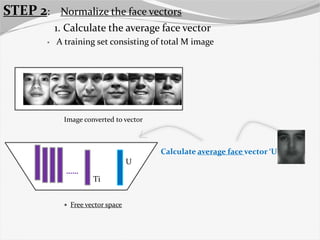
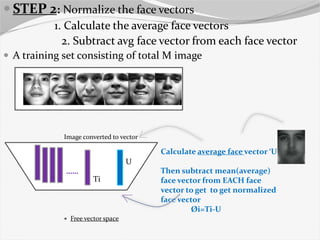
A training set consisting of total M image
Image converted to vector
……
 Free vector space
To calculate the eigenvectors ,
we need to calculate the
covariance vector C
C=A.AT
where A=[Ø1, Ø2, Ø3,… ØM]
N2 X M
Ti
U

12. STEP 3: Calculate the Eigenvectors
 A training set consisting of total M image
Image converted to vector
……
Ti
 Free vector space
U
C=A.AT
N2 X M M X N2 = N2 XN2
Very huge
matrix

13. STEP 3: Calculate the Eigenvectors
 A training set consisting of total M image
Image converted to vector
……
Ti
 Free vector space
U
C=A.AT
N2 eigenvectors
……
N2 X M MX N2 = N2 X N2
Very huge
matrix

14. STEP 3: Calculate the Eigenvectors
A training set consisting of total M image
Image converted to vector


……
Ti
 Free vector space
U
N2 eigenvectors
……
But we need to find only K
eigenvectors from the above
N2 eigenvectors, where K<M
Eg. If N=50 and K=100 , we
need to find 100 eigenvectors
from 2500 (i.e.N2 ) VERY TIME
CONSUMING

15. STEP 3: Calculate the Eigenvectors
A training set consisting of total M image
Image converted to vector


……
Ti
 Free vector space
U
N2 eigenvectors
……
SOLUTION
“DIMENSIONALITY
REDUCTION”
i.e. Calculate eigenvectors from
a covariance of reduced
dimensionality

16. STEP 4: Calculating eigenvectors from reduced
covariance matrix
 A training set consisting of total M image
Image converted to vector


……
Ti
 Free vector space
U
M2 eigenvectors
……
New C=AT .A
MXN2 N2 X M = M XM
matrix

17.  STEP 5: Select K best eigenfaces such that
K<=M and can represent the whole training
set
 Selected K eigenfaces MUST be in the ORIGINAL dimensionality of
the face Vector Space

18. STEP 6: Convert lower dimension K eigenvectors to
original face dimensionality
 A training set consisting of total M image
Image converted to vector

……

Ti
 Free vector space
U
ui = A vi
ui = ith eigenvector in
the higher dimensional
space
vi = ith eigenvector in
the lower dimensional
space
100 eigenvectors
……

19. 2500 eigenvectors
……
Each 2500 X 1
ui = A vi
100 eigenvectors
……
= A
ui
vi
Each 100 X 1 dimension
dimension

20. 2500 eigenvectors
ui
……
Each 2500 X 1
dimension
yellow color shows K selected eigenfaces = ui

21. STEP 6: Represent each face image a linear
combination of all K eigenvectors
Σ
w of mean face
w1
Ω= w2
:
wk
w1 w2 w3 w4 …. wk
We can say, the above image contains a little bit proportion of all these
eigenfaces.

22. Calculating weight of each
eigenfaces
 The formula for calculating the weight is:
wi= Øi. Ui
For Eg.
 w1= Ø1. U1
 w2= Ø2. U2

23. Recognizing an unknown face
r1
r2
:
rk
Convert the
input image
to a face
vector
Normalize
the face
vector
a1 – m1
i a2 – m2
. .
. .
a3 – m3
Project
Normalized face
onto the
eigenspace
w1
Ω= w2
:
wk
Weight vector of
input image
Is
Distanc
e €>
threshol
d∂ ? UNKNOWN FACE
Input image of
UNKNOWN FACE
YES NO
Calculate Distance
between input weight
vector and all the weight
vector of training set
€=|Ω–Ωi|2
i=1…M
RECOGNIZED AS

24. Strengths
It has the ability to leverage existing image
acquisition equipment.
 It can search against static images such as driver’s
license photographs.
 It is the only biometric able to operate without
user cooperation.
10/17/2014 24

25. Weaknesses
Changes in acquisition environment reduce
matching accuracy.
 Changes in physiological characteristics reduce
matching accuracy.
 It has the potential for privacy abuse due to non
cooperative enrollment and identification
capabilities.
10/17/2014 25

26. Applications..

27. Applications
Access Control
Face Databases
Face ID
HCI - Human
Computer
Interaction
Law Enforcement
Day Care
Voter verification
Banking using
ATM

28. Applications
Multimedia
Management
Security
Smart Cards
Surveillance
Security/Countert
errorism
Residential
Security

29. Conclusion
 an algorithm to recognize faces present in the face
database. The proposed algorithm uses
 the concept of PCA and represents an improved
version of PCA to deal with the problem of
orientation and
10/17/2014 29

30. Sources:
[1]http://whatis.techtarget.com/definition/facial-recognition
[2]http://en.wikipedia.org/wiki/Facial_recognition_system
[3]http://sebastianraschka.com/Articles/2014_pca_step_by_s
tep.html
[4]M. Lam, H. Yan, An analytic-to-holistic approach for face
recognition based on a single frontal view, IEEE Trans.
Pattern Anal. Mach. Intel. 20 (1998) 673-686.
[5]Zhang, Automatic adaptation of a face model using action
units for semantic coding of videophone sequences, IEEE
Trans. Circuits Systems Video Technol. 8 (6) (1998) 781-
795.

31. THANK YOU