Face recognition v1

Properties of Face
Id: 1 Id: 1
Id: 1 Id: 2
Intra-variance
Inter-variance

Properties of Face
Makeup
Pose
Large intra-variance

Properties of Face
Small inter-variance

Properties of Face
Diverse Recognition Scenes
Adopted from [8].

Properties of Face
Prior: face images lie on a manifold [15-17]
Adopted from [15]

Holistic learning
Eigenfaces [1][2]
Adopted from Wikipedia(Eigenface)
Fisherfaces [2]
Adopted from OpenCV Docs.(Face Recognition)
Bayes, Laplacianface 2DPCA, SRC, CRC, Metric Learning, etc.

Local handcraft
Gabor filter [3]
Adopted from Mathworks.com
(Gabor Feature Extraction)
Local Binary Pattern [4][5][6]
Adopted from Scikit-image (Local Binary Pattern for texture classification).
EBGM, LGBP, HD-LBP, etc.

Deep learning
DeepFace (Facebook, CVPR 2014)[7]
Adopted from [7].

Training, evaluation protocol
Training protocol,
Evaluation protocol
Adopted from [9].

Training, Evaluation protocol
Adopted from [8].

Training set
Test set
Training set
Probe set
Gallery set
Training set
Test set
Dataset type 1 Dataset type 2 Dataset type 3
Ids in training set
= Ids in test set
Ids in training set
!= Ids in test set.
Info. of matched and
mismatched pairs for
verification
Ids in training set
!= Ids in test set
(for identification)
Dataset type 4
Ids in training set
!= Ids in test set &&
Ids in probe set
!= Ids in Gallery set (exist)
(for identification)
Training set
Probe set
Gallery set

Training, evaluation protocol (Verification)
Training set
Test set
Training set
Probe set
Gallery set
type 2 type 3
Info. of matched and mismatched pairs for
verification.
i.e. pairs_test.txt in LFW dataset.
George_W_Bush 10 24
George_W_Bush 12 John_Kerry 8
Matched pair
Mismatched pair
LFW provides 10 sets for the test.
A set is consist of 300 matched pairs and 300
mismatched pairs.

Training, evaluation protocol (Verification)
Training, Evaluation protocol for LFW dataset
Adopted from [11].
1. Unrestricted, Labeled Outside Data
2. Unrestricted, No Outside Data
Commonly,

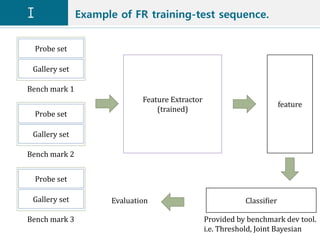
Training, evaluation protocol (Identification)
Training set
Probe set
Gallery set
type 3
Training set
Probe set
Gallery set
type 4
Close-set Identification Adopted from [8].
Open-set Identification Adopted from [8].

Dataset
Long tail distribution
Adopted from [8].
• The depth of dataset enforces the trained model to address a wide range
intra-class variations, such as lighting, age, and pose.
• The breadth of dataset ensures the trained model to cover the sufficiently
variable appearance of various people.

Dataset (training)
The commonly used FR datasets for training.
Adopted from [8].

Dataset (test)
The commonly used FR datasets for test. Adopted from [8].

Evaluation metrics (Face verification)
• Receiver operating characteristic (ROC)
• measures the true accept rate (TAR; TPR) when false
accept rate(FAR; FPR) is kept in a very low rate in most
security certification scenario.
• i.e. PaSC : TAR@10−2FAR, IJB-A : TAR@10−3FAR,
Megaface : TAR@10−6FAR, MS-celeb-1M challenge 3:
TAR@10−9FAR
• Mean accuracy(ACC)
• Represents the percentage of correct classifications.

Evaluation metrics (Identification. Close-set)
• Rank-N
• Rank-N is based on what percentage of probe searches
return the probe’s gallery mate within the top k rank-
ordered results.
• IJB-A/B/C concern on the rank-1 and rank-5 recognition
rate.
• Cumulative match characteristic(CMC)
• CMC curve reports the percentage of probes identified
within a given rank (the independent variable).
• MegaFace challenge systematically evaluates rank-1
recognition rate function of increasing number of gallery
distractors (going from 10 to 1 M)

Evaluation metrics (Identification. Close-set)
• Precision-coverage curve
• Measure identification performance under a variable
threshold t.
• The probe is rejected when its confidence score is lower
than t.
• The algorithms are compared in term of what fraction of
passed probes, i.e. coverage, with a high recognition
precision, e.g. 95% or 99%.
CMC curve. Adopted from [9][12] CMC curve. Adopted from [13]

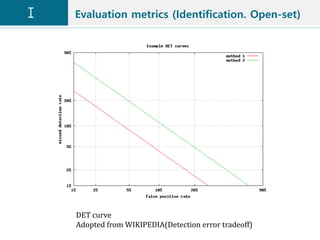
Evaluation metrics (Identification. Open-set)
• Decision(or Detection) error tradeoff (DET) curve [14]
• Characterize the false negative identification rate(FNIR)
as function of false positive identification rate(FPIR).
• The FPIR measures what fraction of comparisons
between probe templates and non-mate gallery
templates result in a match score exceeding T. At the
same time, the FNIR measures what fraction of probe
searches will fail to match a mated gallery template
above a score of T.
• The algorithms are compared in term of the FNIR at a
low FPIR, e.g. 1% or 10%.
• IJB-A benchmark supports open-set face recognition.

Evaluation metrics (Identification. Open-set)
DET curve
Adopted from WIKIPEDIA(Detection error tradeoff)

Example of FR training-test sequence.
Training set
Probe set
Gallery set
Large scale dataset
Feature Extractor
Lose
function
for training
feature
extractor

Probe set
Gallery set
Bench mark 3
Feature Extractor
(trained)
feature
Probe set
Gallery set
Bench mark 2
Probe set
Gallery set
Bench mark 1
Evaluation
Provided by benchmark dev tool.
i.e. Threshold, Joint Bayesian
Classifier

Feature Extractor
(trained)
Classifier
(i.e. Metric learning,
SRC)Bench mark 1
Training set
Probe set
Gallery set
Bench mark 2
Training set
Probe set
Gallery set Fine-tuning (transfer learning)

Deep FR System
Deep FR System
Adopted from [8].
K. Zhang, Z. Zhang, Z. Li, Y. Qiao. Joint face detection and alignment using multi-task
cascaded convolutional networks. arXiv preprint arXiv:1604.02878, 2016

Deep FR System
Adopted from [8].

Deep Face (Facebook, CVPR, 2014)
Face Alignment
Adopted from [7].

Outline of the DeepFace architecture
Adopted from [7].
Dataset for training: Social Face Classification (SFC) dataset
(4.4M labeled face, 4K identities, 800~1200 faces per person)
Objective: Minimize cross entropy with softmax function.

• Verification metric
• Weighted 𝜒2 distance
• DeepFace feature vector contains several similarities
to histogram-based feature.[6]
1. It contains non-negative values
2. It is very sparse
3. Its values are between [0, 1].
• 𝜒2
𝑓1, 𝑓2 = 𝑖
𝑤 𝑖 𝑓1 𝑖 −𝑓2 𝑖 2
𝑓1 𝑖 +𝑓2[𝑖]
• The weight parameters are learned using a linear
SVM.
• Siamese network [18]
• Metric learning
• 𝑑 𝑓1, 𝑓2 = 𝑖 𝛼𝑖|𝑓1 𝑖 − 𝑓2 𝑖 |

Adopted from [18].

Comparison of the classification errors on the SFC.
Adopted from [7].
• DF-1.5K, 3.3K, 4.4K: Subsets of sizes 1.5K, 3K, 4K persons
• DF-10%, 20%, 50%: the global number of samples in SFC to
10%, 20%, 50%
• DF-sub1, sub2, sub3: chopping off the C3, L4, L5 layers.

The performance of various individual DeepFace networks and
the Siamese network.
Adopted from [7].
• DeepFace-single: 3D aligned RGB inputs
• DeepFace-align2D: 2D aligned RGB inputs.
• DeepFace-gradient: gray-level image plus image gradient
magnitude and orientation.
• DeepFace-ensemple: combined distances using a non-linear
SVM with a simple sum of power CPD-kernels.

Comparison with the state-of-the-art on the LFW dataset.
Adopted from [7].
• DeepFace-single, unsupervised: directly compare the inner
product of a pair of normalized features.

• DeepFace-single, unsupervised(95.92%): directly compare
the inner product of a pair of normalized features.
• DeepFace-single, restricted(97%): 5,400 pair labels for
training, kernel-SVM.
• DeepFace-ensemble, restricted (97.15%):
single+gradient+align2d
• DeepFace-ensemble, unrestricted 1 (97.25%):
single+gradient+align2d+Siamese
• DeepFace-ensemble, unrestricted 2 (97.35%): 5 single +
gradient + align2d + Siamese

Comparison with the state-of-the-art on the LFW dataset.
Adopted from [7].

DeepID2 (CUHK, NIPS, 2014)
𝑉𝑒𝑟𝑖𝑓 𝑓𝑖, 𝑓𝑖, 𝑦𝑖𝑗, 𝜃𝑣𝑒 =
1
2
𝑓𝑖 − 𝑓𝑗 2
2
𝑖𝑓 𝑦𝑖𝑗 = 1
1
2
max 0, 𝑚 − 𝑓𝑖 − 𝑓𝑗 2
2
𝑖𝑓 𝑦𝑖𝑗 = −1
𝐼𝑑𝑒𝑛𝑡 𝑓, 𝑡, 𝜃𝑖𝑑 = −
𝑖=1
𝑛
𝑝𝑖 log 𝑝𝑖 = − log 𝑝𝑡
𝑉𝑒𝑟𝑖𝑓 𝑓𝑖, 𝑓𝑖, 𝑦𝑖𝑗, 𝜃𝑣𝑒 =
1
2
𝑦𝑖𝑗 − 𝜎 𝑤𝑑 + 𝑏
2
𝑑 =
𝑓𝑖 ⋅ 𝑓𝑗
𝑓𝑖 2 𝑓𝑗 2

The DeepID2 feature learning algorithm.
Adopted from [19].

Patches selected for feature extraction.(positions, scales, color
channels, horizontal flipping)
Adopted from [19].
The ConvNet structure for DeepID2 feature extraction.
Adopted from [19].

400 patches
⋯
⋯
200 network
Feature
selection and
concat (25
network)
4000 dim 180 dim
PCA
Joint
Bayesian
Dataset: CelebFaces+ (0.2M, 10K) -> (8192K)
8192 ID(training), 1985 ID(validation)
1985 ID(validation)->1485 ID(training), 500 ID(validation)

(left)Face verification accuracy by varying the weighting
parameter 𝜆.
(right) Face verification accuracy of DeepID2 features learned by
both the face identification and verification signals, where the
number of training identities used for face identification varies.
Adopted from [19].

Spectrum of eigenvalues of the inter- and intra-personal scatter
matrices.
Adopted from [19].

The first two PCA dimensions of DeepID2 features extracted from
six identities in LFW.
Adopted from [19].
Comparison of different verification signals. (classifying the 8192
identities)
Adopted from [19].

Face verification accuracy with DeepID2 features extracted from
an increasing number of face patches.
Adopted from [19].
Accuracy comparison with the previous best results on LFW.
Adopted from [19].

ROC comparison with the previous best results on LFW.
Adopted from [19].

DeepID3 (CUHK, arXiv, 2015)
Architecture of DeepID3.
Adopted from [19].

Architecture of DeepID3.
Adopted from [20].

Face verification on LFW.
Adopted from [20].
50 networks.
VGGNet-10

FaceNet (Google, CVPR, 2015)
Adopted from [21].

𝒯 is the set of all possible triplets in the training
set and has cardinality N.
𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑝
2
2
+ 𝛼 < 𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑛
2
2
∀ 𝑓 𝑥𝑖
𝑎
, 𝑓 𝑥𝑖
𝑝
, 𝑓 𝑥𝑖
𝑛
∈ 𝒯
ℒ =
𝑖
𝑁
𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑝
2
2
− 𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑛
2
2
+ 𝛼
+
𝑓 𝑥 ∈ ℝ 𝑑
Constrain embedding to live on the d-dimensional hypersphere.
i.e. 𝑓 𝑥 2 = 1

Triplet Selection
Given 𝑥𝑖
𝑎
,
Hard positive: 𝑎𝑟𝑔𝑚𝑎𝑥 𝑥 𝑖
𝑝 𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑝
2
2
Hard negative: 𝑎𝑟𝑔𝑚𝑖𝑛 𝑥 𝑖
𝑛 𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑛
2
2
Infeasible to compute the argmin and argmax across the
whole training set.
Might lead to poor training, as mislabeled and poorly imaged
faces would dominate the hard positives and negatives.

Triplet Selection
Given 𝑥𝑖
𝑎
,
Semi-hard negative
𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑝
2
2
< 𝑓 𝑥𝑖
𝑎
− 𝑓 𝑥𝑖
𝑛
2
2
𝑓 𝑥𝑖
𝑝
𝑓 𝑥𝑖
𝑎
𝑓 𝑥𝑖
𝑛
𝑓 𝑥𝑖
𝑎
𝛼

Triplet Selection
• Generate triplets offline every n steps,
using the most recent network checkpoint
and computing the argmin and argmax on
a subset of the data.
• Generate triplets online. This can be done
by selecting the hard positive/negative
exemplars from within a mini-batch.

Dataset: Google (500M, 10M)
Network: Inception 224x224
LFW
98.87% ± 0.15 using fixed center crop.
99.63% ± 0.09 using the extra face alignment.

Center Loss (SIAT, ECCV, 2016)
The distribution of deeply learned features in (a) training set (b) testing set, both under
the supervision of softmax loss.
Adopted from [22].

ℒ 𝐶 =
1
2
𝑖=1
𝑚
𝑥𝑖 − 𝑐 𝑦 𝑖 2
2
𝑥𝑖: 𝑖th deep feature belonging to the 𝑦𝑖th class.
𝑐 𝑦 𝑖
: 𝑦𝑖th class center of deep features.
The center loss and its variant suffer from massive GPU memory
consumption on the classification layer, and prefer balanced and
sufficient training data for each identity.

ℒ = ℒ 𝑆 + 𝜆ℒ 𝐶
= −
𝑖=1
𝑚
log
𝑒 𝑊𝑦 𝑖
𝑇 𝑥 𝑖+𝑏 𝑦 𝑖
𝑗=1
𝑛
𝑒 𝑊𝑗
𝑇 𝑥 𝑖+𝑏 𝑗
+
𝜆
2
𝑖=1
𝑚
𝑥𝑖 − 𝑐 𝑦 𝑖 2
2

The distribution of deeply learned features under the joint supervision of softmax loss
and center loss.
Adopted from [22].

Adopted from [22].

Face verification accuracies on LFW dataset, respectively achieve by (a) models with
different 𝜆 and fixed 𝛼 = 0.5. (b) models with different 𝛼 and fixed 𝜆 = 0.003.
Adopted from [22].

A: softmax
B:softmax+contrastive
C: proposed. 𝜆 = 0.003, 𝛼 = 0.5
Adopted from [22].

L-Softmax (Peking univ. , ICML, 2016)
Original softmax loss 𝐿 =
1
𝑁
𝑖
𝐿𝑖 =
1
𝑁
𝑖
− log(
𝑒 𝑓𝑦 𝑖
𝑗 𝑒 𝑓 𝑗
)
𝑥𝑖: 𝑖-th input feature, 𝑦𝑖:label, N: the number of training
data, 𝑓𝑗: 𝑗-th element of the vector of class scores 𝒇.
𝑓 is usually the activations of a fully connected layer 𝑾, so 𝑓𝑦 𝑖
can be written
as 𝑓𝑦 𝑖
= 𝑾 𝑦 𝑖
𝑇
𝒙𝑖 in which 𝑾 𝑦 𝑖
𝑇
is 𝑦𝑖-th column of 𝑾.
𝑾 𝒙 𝑏 𝒇
𝑠𝑜𝑓𝑡𝑚𝑎𝑥 𝑐𝑟𝑜𝑠𝑠 𝑒𝑛𝑡𝑟𝑜𝑝𝑦
𝑾 𝑦 𝑖
𝑓𝑦 𝑖

𝑓𝑗 = 𝑾𝑗
𝑇
𝒙𝑖 = 𝑾𝑗
𝑇
𝒙𝑖 cos(𝜃𝑗) where 𝜃𝑗(0 ≤ 𝜃𝑗 ≤ 𝜋) is the angle between the
vector 𝑾𝑗
𝑇
and 𝒙𝑖.
𝐿𝑖 = − log
𝑒
𝑾 𝑦 𝑖
𝑇 𝒙𝑖 cos 𝜃 𝑦 𝑖
𝑗 𝑒
𝑾 𝑗
𝑇 𝒙 𝑖 cos 𝜃 𝑗
In the binary classification, if we have a sample 𝒙 from class 1.
𝑾1 𝒙 cos 𝜃1 > 𝑾2 𝒙 cos 𝜃2
𝑾1 𝒙 cos 𝑚𝜃1 > 𝑾2 𝒙 cos 𝜃2 (0 ≤ 𝜃1 ≤
𝜋
𝑚
) where 𝑚 is a positive integer.
𝑾1 𝒙 cos 𝜃1 ≥ 𝑾1 𝒙 cos 𝑚𝜃1 > 𝑾2 𝒙 cos 𝜃2

𝐿𝑖 = − log
𝑒
𝑾 𝑦 𝑖
𝑇 𝒙𝑖 𝜓(𝜃 𝑦 𝑖
)
𝑒
𝑾 𝑦 𝑖
𝑇 𝒙𝑖 𝜓(𝜃 𝑦 𝑖
)
+ 𝑗≠𝑦 𝑖
𝑒
𝑾 𝑗
𝑇 𝒙𝑖 cos 𝜃 𝑗
𝜓 𝜃 = −1 𝑘
cos 𝑚𝜃 − 2𝑘, 𝜃 ∈
𝑘𝜋
𝑚
,
𝑘 + 1 𝜋
𝑚
𝑘 ∈ [0, 𝑚 − 1]
Adopted from [23].

Adopted from [23].
𝑓𝑦 𝑖
=
𝜆 𝑊𝑦 𝑖
𝑥𝑖 cos 𝜃 𝑦 𝑖
+ 𝑊𝑦 𝑖
𝑥𝑖 𝜓 𝜃 𝑦 𝑖
1 + 𝜆

Adopted from [23].
cos(𝑛𝑥) =
𝑘=0
𝑛
2
−1 𝑘 𝑛
2𝑘
sin2 𝑥 𝑘 cos 𝑛−2𝑘(𝑥)
=
𝑘=0
𝑛
2
−1 𝑘 𝑛
2𝑘
1 − cos2
𝑥 𝑘
cos 𝑛−2𝑘
(𝑥)
For forward and backward propagation, we need to replace cos(𝜃𝑗) with
𝑾 𝑗
𝑇
𝒙 𝑖
𝑾 𝑗
𝑇 𝒙𝑖
cos(𝑚𝜃 𝑦 𝑖
)
=
𝑚
0
cos 𝑚(𝜃 𝑦 𝑖
) −
𝑚
2
cos 𝑚−2 𝜃 𝑦 𝑖
1 − cos2 𝜃 𝑦 𝑖
+
𝑚
4
cos 𝑚−4 𝜃 𝑦 𝑖
1 − cos2 𝜃 𝑦 𝑖
2
+ ⋯ −1 𝑛 𝑚
2𝑛
cos 𝑚−2𝑛
𝜃 𝑦 𝑖
1 − cos2
𝜃 𝑦 𝑖
𝑛
+ ⋯
Where 𝑛 is an integer and 2𝑛 ≤ 𝑚.

Adopted from [23].

SphereFace (Georgia Tech. , CVPR, 2017)
Adopted from [24].
𝐿𝑖 = − log
𝑒 𝒙𝑖 𝜓(𝜃 𝑦 𝑖
)
𝑒 𝒙𝑖 𝜓(𝜃 𝑦 𝑖
)
+ 𝑗≠𝑦 𝑖
𝑒 𝒙 𝑖 cos 𝜃 𝑗
𝜓 𝜃 = −1 𝑘 cos 𝑚𝜃 − 2𝑘, 𝜃 ∈
𝑘𝜋
𝑚
,
𝑘 + 1 𝜋
𝑚
𝑘 ∈ [0, 𝑚 − 1]
In the binary classification.
𝑾1 = 𝑾2 = 1

Adopted from [24].

Experiments on LFW and YTF.
Adopted from [24].

MegaFace.
Adopted from [24].

Experiments on MegaFace
Adopted from [24].

1:1M rank-1 identification results on MegaFace benchmark: (a)
introducing label flips to training data, (b) introducing outliers to
training data.
Adopted from [26].

CosFace (Tencent AI Lab, arXiv, 2018)
Adopted from [25].

L2-normalization, scaling
Adopted from [27].

ArcFace (Imperial College, arXiv, 2018)
Adopted from [28].

References
[1] M. Turk, A. Pentland, “Face recognition using eigenfaces,” in Proc. CVPR, pp.
586–591. (1991)
[2] P. Belhumeur, J. P. Hespanha, and D. Kriegman. “Eigenfaces vs. fisherfaces:
Recognition using class specific linear projection,” in PAMI, 19(7):711-720, July
1997.
[3] H. G. Feichtinger, T. Strohmer, “Gabor Analysis and Algorithms,” in Birkhauser,
1998.
[4] DC. He, L. Wang, “Texture Unit, Texture Spectrum, And Texture Analysis,” in
IEEE Trans. Geoscience and Remote Sensing, Vol. 8, No. 8, pp. 905-910, 1990.
[5] L. Wang, DC. He, “Texture Classification Using Texture Spectrum,” in Pattern
Recognition, Vol. 23, No. 8, pp. 905-910, 1990.
[6] T. Ahonen, A. Hadid, and M. Pietikainen, “Face description with local binary
patterns: Application to face recognition,” in PAMI, 2006
[7] Y. Taigman, M. Yang, M. Ranzato, L. Wolf, “DeepFace: Closing the gap to human-
level performance in face verification,” in Proc. CVPR, 2014
[8] M. Wang, W. Deng, “Deep Face Recognition: A Survey,” ArXiv preprint
arXiv:1804.06655v8
[9] W. Liu, Y. Wen, Z. Yu, M. Li, B. Raj, L. Song, SphereFace: Deep Hypersphere
Embedding for Face Recognition. In Conf. on CVPR, 2017

References
[10] G. B. Huang, M. Ramesh, T. Berg, E. Learned-Miller. Labeled Faces in the Wild:
A Database for Studying Face Recognition in Unconstrained Environments.
University of Massachusetts, Amherst, Technical Report 07-49, October, 2007.
[11] G. B. Huang, E. Learned-Miller. Labeled Faces in the Wild: Updates and New
Reporting Procedures.
[12] J. Deng, J. Guo, S. Zafeiriou. Arcface: Additive angular margin loss for deep
face recognition. arXiv preprint arXiv:1712.04695, 2017
[13] F. Zhao & Y. Jian, Y. Shuicheng, J. Feng. Dynamic Conditional Networks for
Few-Shot Learning. ECCV, 2018
[14] B. K. Klare, B. Klein, E. Taborsky, A. Blanton, J. Cheney, K. Allen, P. Grother, A.
Mah, K. Jain. Pushing the Frontiers of Unconstrained Face Detection and
Recognition: IARPA Janus Benchmark A. CVPR, 2015
[15] A. Talwalkar, S. Kumar, H. Rowley. Large-scale manifold learning. In CVPR,
2014
[16] K. –C. Lee, J. Ho, M. –H. Yang, D. Kriegman. Video-based face recognition using
probabilistic appearance minifolds. In CVPR, 2003.
[17] X. He, S. Yan, Y. Hu, P. Niyogi, H.-J. Zhang. “Face recognition using
laplacianfaces,” PAMI, 27(3):328-240.
[18] S. Chopra, R. Hadsell, Y. LeCun. Learning a similarity metric discriminatively,
with application to face verification. In CVPR, 2005.

References
[19] Y. Sun, Y. Chen, X. Wang, X. Tang. Deep learning face representation by joint
identification-verification. In NIPS, pages 1988-1996, 2014.
[20] Y. Sun, D. Liang, X. Wang, X. Tang. Deepid3: Face recognition with very deep
neural networks. arXiv preprint arXiv:1502.00873
[21] F. Schroff, D. Kalenichenko, J. Philbin. Facenet: A unified embedding for face
recognition and clustering. In CVPR, pp. 815-823, 2015.
[22] Y. Wen, K. Zhang, Z. Li, Y. Qiao. A discriminative feature learning approach for
deep face recognition. In ECCV, pp 299-515, 2016.
[23] W. Liu, Y. Wen, Z. Yu, M. Yang. Large-margin softmax loss for convolutional
neural networks. In ICML, pp. 507-516, 2016.
[24] W. Liu, Y. Wen, Z. Yu, M. Li, B. Raj, L. Song. Sphererface: Deep hypersphere
embedding for face recognition. In CVPR, volume 1, 2017.
[25] F. Wang, W. Liu, H. Liu, J. Cheng. Additive margin softmax for face verification.
arXiv preprint arXiv:1801.05599, 2018
[26] F. Wang, L. Chen, C. Li, S. Huang, Y. Chen, C. Qian, C. Change Loy. The devil of
face recognition is in the noise. In ECCV, September 2018.
[27] R. Ranjan, C. D. Castillo, R. Chellappa. L2-constrained softmax loss for
discriminative face verification. arXiv preprint arXiv:1703.09507, 2017.
[28] J. Deng, J. Guo, S. Zafeiriou. Arcface: Additive angular margin loss for deep
face recognition .arXiv:1801.07698, 2018.

Face recognition v1

More Related Content

What's hot

Similar to Face recognition v1

More from San Kim

Recently uploaded

Face recognition v1

Editor's Notes