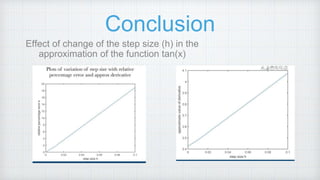
This document discusses error analysis in numerical computation. It contains: 1) An introduction discussing types of computational errors like rounding off and truncation errors. 2) A MATLAB program to calculate the exponential function using Taylor series expansion and evaluate the absolute and relative errors. 3) A second program to approximate the derivative of tan(x) at different step sizes and calculate the relative percentage error, showing the error decreases with smaller step sizes. 4) Conclusions about how the approximation accuracy improves with decreasing step size due to reducing truncation error, with round-off error dominating at very small step sizes.

1. PRACTICAL
Name- Saloni Singhal
M.Sc. (Statistics) II-Sem.
Roll No: 2046398
Course- MATH-409 L
Numerical Analysis Lab
Submitted To: Dr. S.C. Pandey
1.3

2. OBJECTIVE
Error Analysis in Computation: Round Off
and Truncation Errors
Problem Statement
1.Write a program (script file) for computation of Exponential function ex up to
4 terms in its series expansion. Calculate the value (true value of ex at x=0.001)
2.Evaluate the error in the computation of ex at x=0.001 (absolute error and
fractional relative error in percentage.)
3. Approximate the first derivative of tan(x) at x =1, and evaluate its relative
percentage error.

3. Theory
Computational Errors:
• Rounding off error occur as machine has limited capacity to store
exact number.
• For example: rational number having finite number of digits.
• The accumulated effect become significant after repeated operations.
They are of two types: 1.chopping
2.symmetry round off
• Truncation error arises when exact mathematical procedure is
approximated and process is truncated after a finite number of
iterations for computational simplicity.
• Example: when infinite series is to be added to arrive at exact result

4. Program
>> format long
>> n=0;
x=0.001;
y=0;
%expanding taylor series for ex
>> while n<=4
a=x^n/factorial(n);
n=n+1; y=y+a
end
y =
1
y =
1.001000000000000
y =
1.001000500000000

5. Program
Contd.
y =
1.001000500166667
y =
1.001000500166708
>> truevav=exp(0.001)
truevav =
1.001000500166708
>> err=abs(truevav-y)
err =
0

6. Error Analysis
As h grows smaller and smaller, f[x + h, x − h]
becomes a better and better approximation to
f(x) .If we plot the truncation error against h on a
log- scale (for linearity), we expect to see a
straight line. For small h values, the error is
dominated by roundoff rather than by truncation
error. An advantage of the higher order of
accuracy is that we can get very small truncation
errors even when h is not very small, and so we
tend to be able to reach a better optimal error
before cancellation effects start to dominate.

7. 2. Program Contd.
h=zeros(5,1)
%initial zero matrix for approximated value
approxval=zeros(5,1)
err=zeros(5,1)
e=zeros(5,1)
format long
for i=1:5; x=1;
h(i)=10^(-i);
trueval=(sec(x))^2;
%numerical diffential
approxval(i)=(tan(x+h(i))-tan(x))/h(i);
%relative error
err(i)=abs(trueval-approxval(i))
e(i)=(err(i)/trueval)*100
end
Another way to create a
matrix is to use a function,
such as ones, zeros,
or rand.

8. Conclusion
Effect of change of the step size (h) in the
approximation of the function tan(x)

9. Error Analysis
The secant of a function based at a and a +h, as well as the tangent at a.
h ( f (a +h)− f (a))/h E(f ;a,h)
10−1 4.073519 -0.6480711
10−2 3.4798299 -0.053110792
10−3 3.4308632 -0.00534437
10−4 3.4260524 -0.0053357
10−5 3.4255721 -5.37919*10−5
Round Off Error: E(f ;a,h) = f’(a)− f (a+h)− f (a) /h. We observe
that the approximation improves with decreasing h, as expected.
More precisely, when h is reduced by a factor of 10, the error is
reduced by the same factor.

10. Truncation Error
Expansion of f (a +h) about x = a using Taylor expansion, where ξh lies
in the interval (a,a+h). The formula may be rearranged to give an
expression for the error often referred to as the truncation error of the
approximation. It is bounded as:
Optimum step size(h)
Total error is given by:
To find the value of h which minimizes this expression, we differentiate with
respect to h and set the derivative to zero. We find 0 (h) = 0, we obtain the
approximate optimal value of h

11. References
• Class Codes by Prof. S.C. Pandey Sir
• MATLAB documentation
• Numerical Differentiation e-notes
• Introduction to Scientific Computing (CS 3220)
Bindel, Spring. 2012