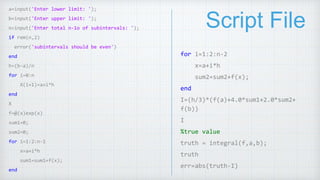
1. The document describes implementing Simpson's 1/3 rule to numerically evaluate integrals using MATLAB. 2. Simpson's 1/3 rule uses a second-order polynomial to fit 3 points, allowing the integral over 3 subintervals to be approximated. It requires an even number of subintervals. 3. The MATLAB script calculates the integral of an example function exp(x) over intervals [a,b] divided into n subintervals using Simpson's 1/3 rule and compares the result to the true integral value.

1. PRACTICAL
Name- Saloni Singhal
M.Sc. (Statistics) II-Sem.
Roll No: 2046398
Course- MATH-409 L
Numerical Analysis Lab
Submitted To: Dr. S.C. Pandey

2. OBJECTIVE
1. Create an M-file to implement
Simpson’s One-Third Rule.

3. Theory
Simpson’s 1/3 rule corresponds to using second-order
polynomials. Using the Lagrange form for a quadratic fit of
three points.
Integration over the three points amplifies to:
Simpson’s 1/3 rule can be used on a set
of subintervals in much the same way
the trapezoidal rule was, except there
must be an odd number of points

4. Error in Trapezoidal
Rule
Local Error
Global Error
Global Error O(h4)is sum total of all n/2 local
error and is of an order less than Local error
O(h5)

5. Script File
a=input('Enter lower limit: ');
b=input('Enter upper limit: ');
n=input('Enter total n-1o of subintervals: ');
if rem(n,2)
error('subintervals should be even')
end
h=(b-a)/n
for i=0:n
X(i+1)=a+i*h
end
X
f=@(x)exp(x)
sum1=0;
sum2=0;
for i=1:2:n-1
x=a+i*h
sum1=sum1+f(x);
end
for i=1:2:n-2
x=a+i*h
sum2=sum2+f(x);
end
I=(h/3)*(f(a)+4.0*sum1+2.0*sum2+
f(b))
I
%true value
truth = integral(f,a,b);
truth
err=abs(truth-I)

6. Output

7. Conclusion
• Error is dependent upon the fourth-derivative of the
actual function as well as the distance between the
points.
• Error is dependent on the fifth power of the step size
(rather than the third for the trapezoidal rule).
• Error can thus be reduced by breaking the curve into
parts
• 1/3rd S.R. requires the even number of intervals or
odd number of ordinates

8. Caveats
• This gives a better approximation than the previous
methods. However, since 3 points are required to define a
parabola,
an even number of strips is required for the formula to
work.
• Simpson’s 3/8 rule is generally used in concert with
Simpson’s 1/3 rule when the number of
segments is odd.

9. References
http://www.math.umd.edu/~jmr/141/Sim
psonDemo.html
https://nptel.ac.in/courses/111/107/1111
07062/ Module:Numerical Integration
Class Notes of Dr.S.C.Pandey Sir