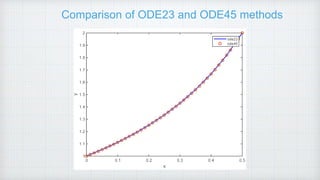
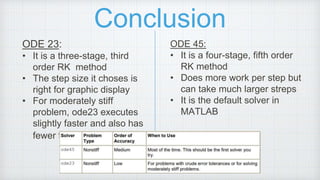
The document outlines the implementation of the Runge-Kutta methods (ode23 and ode45) in MATLAB for solving ordinary differential equations and includes a comparison of their performance. It discusses the step-by-step process of defining a function, setting the domain, and plotting results, highlighting the exact solution as well as the numerical approximations. The conclusion emphasizes the characteristics and advantages of both methods in various scenarios.

1. PRACTICAL
Name- Saloni Singhal
M.Sc. (Statistics) II-Sem.
Roll No: 2046398
Course- MATH-409 L
Numerical Analysis Lab
Submitted To: Dr. S.C. Pandey

2. OBJECTIVE
1. Create an M-file to implement Range Kutta
(ode23, ode45) method for solving ordinary
differential equations
2. Plot the exact and numerical solution.

3. Theory
The functions ode23 and ode45 are the principal MATLAB
tools for solving non-stiff ODE.(An ordinary differential
equation problem is stiff if the solution being sought is varying
slowly, but there are nearby solutions that vary rapidly, so the
numerical method must take small steps to obtain satisfactory
results)
They are also known as Runge-Kutta methods. Each step is almost
independent of the previous steps. Two important pieces of information are
passed from one step to the next. The step size h expected to
achieve a desired accuracy is passed from step to step.

4. Script File
f=@(x,y) x*y^2+y
[x,y] = ode23(f,[0,0.5],1)
plot(x,y,'r','linewidth',1.5)
hold on
xlabel('x')
ylabel('y’)
f=@(x,y) x*y^2+y
[x,y] = ode45(f,[0,0.5],1)
plot(x,y,'r','linewidth',1.5)
hold on
xlabel('x')
ylabel('y')

5. Output
Numerically approximate the solution of the first
order differential equation
Dy/dx = xy2 + y, y(0) = 1, on the interval x ∈ [0,
0.5].
For any differential equation in the form y’= f(x,
y), we begin by defining the function
f(x, y). For single equations, we can define f(x, y)
as an anonymous function. The basic syntax for
the MATLAB solver ode45 is
ode45(Function, Domain, Initial Condition)
For this example, we use
MATLAB returns two column vectors. The first
with values of x and the second with values
of y. Since x and y are vectors with
corresponding components, we can plot the
values with
which creates the figure below

6. the exact solution is y(x) = 1/(1 − x)
ODE23
ODE45

7. Comparison of ODE23 and ODE45 methods

8. Conclusion
ODE 23:
• It is a three-stage, third
order RK method
• The step size it choses is
right for graphic display
• For moderately stiff
problem, ode23 executes
slightly faster and also has
fewer failed steps.
ODE 45:
• It is a four-stage, fifth order
RK method
• Does more work per step but
can take much larger streps
• It is the default solver in
MATLAB

9. References
https://nptel.ac.in/courses/111/107/111107062/
Module: Num Soln of ODE of first order
MATLAB Documentation:
https://blogs.mathworks.com/cleve/2014/05/26/or
dinary-differential-equation-solvers-ode23-and-
ode45/
Class Notes of Dr.S.C.Pandey Sir