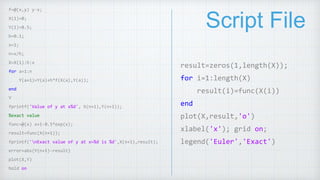
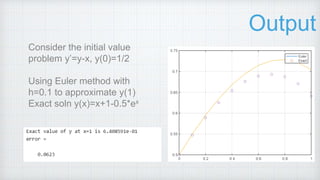
1. The document describes implementing Euler's method for solving ordinary differential equations in MATLAB. 2. It provides the theory behind Euler's method, which uses the first two terms of the Taylor series expansion to approximate solutions with an error term of O(h). 3. The MATLAB script file implements Euler's method to solve the initial value problem y' = y - x, y(0) = 1/2, comparing the numerical solution to the exact solution.

1. PRACTICAL
Name- Saloni Singhal
M.Sc. (Statistics) II-Sem.
Roll No: 2046398
Course- MATH-409 L
Numerical Analysis Lab
Submitted To: Dr. S.C. Pandey

2. OBJECTIVE
1. Create an M-file to implement
Euler’s method for solving ordinary
differential equations
2. Plot the exact and numerical solution.

3. Theory
if we make h small enough, we may only need a few terms of the
Taylor-series expansion for good accuracy. The Euler method
follows this idea to the extreme for first-order differential
equations - it uses only the first two terms of the Taylor series.
Suppose that we have chosen h small enough so that we may
truncate the series after the first derivative term.
where last term is the usual error term for the truncated Taylor
series. Adopting a subscript notation for the successive y-values
and representing the error by the order relation, we may write the
algorithm for Euler’s method in the form
This error is just the local error i.e. error in a single step. Over
many steps, the global error becomes of O (h)

4. Geometric Interpretation
By constructing the
ordinates at x0 and x0+ ℎ . . ,
if we draw the tangent to the
solution
curve at (x0 ,y0) then height
of the ordinate at x1, to the
point of intersection A (say)
of this
tangent and ordinate at x1
gives the value of y at x1 by
Euler method.

5. Script File
f=@(x,y) y-x;
X(1)=0;
Y(1)=0.5;
h=0.1;
x=1;
n=x/h;
X=X(1):h:x
for a=1:n
Y(a+1)=Y(a)+h*f(X(a),Y(a));
end
Y
fprintf('Value of y at x%d', X(n+1),Y(n+1));
%exact value
func=@(x) x+1-0.5*exp(x);
result=func(X(n+1));
fprintf('nExact value of y at x=%d is %d',X(n+1),result);
error=abs(Y(n+1)-result)
plot(X,Y)
hold on
result=zeros(1,length(X));
for i=1:length(X)
result(i)=func(X(i))
end
plot(X,result,'o')
xlabel('x'); grid on;
legend('Euler','Exact')

6. Output
Consider the initial value
problem y’=y-x, y(0)=1/2
Using Euler method with
h=0.1 to approximate y(1)
Exact soln y(x)=x+1-0.5*ex

7. Conclusion
At h=0.05
Decreasing the step size
improves the accuracy of
Euler's method as evident from
the error and plot

8. Caveats
• The trouble with the most simple Euler method is it’s
lack of accuracy, requiring an extremely small step size.
• To overcome this problem, Euler modified his method by
considering one more term of the Taylor series and
expressing the second derivative yn’’ by the forward-
difference approximation.