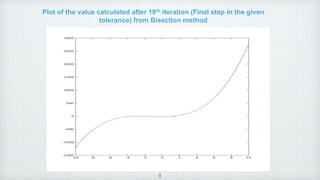
The document describes the implementation of the bisection method for root-finding in numerical analysis, outlining its theoretical basis and algorithmic steps. It includes a script for executing the method in MATLAB, detailing the iterative process for narrowing down to the root of a continuous function. The conclusion emphasizes the method’s simplicity and robustness, while also noting its relative slowness compared to other root-finding methods.

1. PRACTICAL
Name- Saloni Singhal
M.Sc. (Statistics) II-Sem.
Roll No: 2046398
Course- MATH-409 L
Numerical Analysis Lab
Submitted To: Dr. S.C. Pandey
1

2. OBJECTIVE
1. Create an M-file to implement
Bisection method.
2

3. Theory
Root-finding problem: Bisection Method is also called the interval
halving method, the binary search method, or the dichotomy method. is
based on the Bolzano’s theorem for continuous functions.
Intermediate value theorem states that if f is a continuous
function whose domain contains the interval [a, b], then it takes on any
given value between f(a) and f(b) at some point within the interval.
This has two corollaries:
1.If a continuous function has values of opposite sign inside an interval,
then it has a root in that interval (Bolzano's theorem).
2.The image of a continuous function over an interval is itself an interval
3

4. Algorithm
Graphical Interpretation
1.Two values a and b are chosen for which f(a) > 0 and f(b)
< 0 (or the other way around)
2.Bisection: a midpoint c is calculated as the arithmetic
mean between a and b, c = (a + b) / 2
3.The function f is evaluated for the value of c
4.If f(c) = 0 means that we found the root of the function,
which is c
5.If f(c) ≠ 0 we check the sign of f(c):
1.if f(c) has the same sign as f(a) we replace a with c and
we keep the same value for b
2.if f(c) has the same sign as f(b), we replace b with c and
we keep the same value for a
6.We go back to step 2. and recalculate c with the new value
of a or b
We continue in this manner and the process is repeated until
the root is obtained. How close the value of c gets to the real
root depends on the value of the tolerance we set for the
algorithm
4

5. Script File
%define the function
f=@(x)2*x.^3+8*x.^2-20; a=1; b=2; error=10^(-4);
i=1
c=(a+b)/2 %bisection using mean value theorem
d=f(c)
while abs(f(c))>error %defining tolerance
if f(c)<0 && f(a)<0
a=c;
else
b=c;
end
i=i+1
c=(a+b)/2;
d=f(c)
%plot the iterated values using bisection method
x = 1:0.0001:2
plot(c,d,'o');
hold on
end
%plot the final iterated value
plot(c,d,"*")
y=0;
%plot the given function
plot(x, f(x))
z=@(x)0*x;
%plot the x-axis
plot(x,z(x))
hold off
5

6. Output
6

7. Plot of the value calculated after ith iterations in Bisection
method
7

8. Plot of the value calculated after 18th iteration (Final step in the given
tolerance) from Bisection method
8

9. Conclusion
• The final value calculated after iterations is shown in the
second plot
• to calculate an approximate root of a function within tolerance
ε, the number n of iterations we need to perform is at least:
n ≥ log((b−a)/ε)/log(2)
here, n≥ 4/log(2) = 13.28 (in accordance with the number of
iterations n=18)
• Iteration terminates when bound for relative error is less than
tolerance, |p-pn|/min{|an|,|bn|}< 10-4
and sequence pn convergence to p with rate of convergence
O(1/2n)
9

10. Caveats
• Bisection Method is a simple root finding method,
easy to implement and very robust.
• However, the disadvantages of this method is that
it’s relatively slow.
• Because of this, most of the time, the bisection
method is used as a starting point to obtain a rough
value of the solution which is used later as a
starting point for more rapidly converging methods.
10