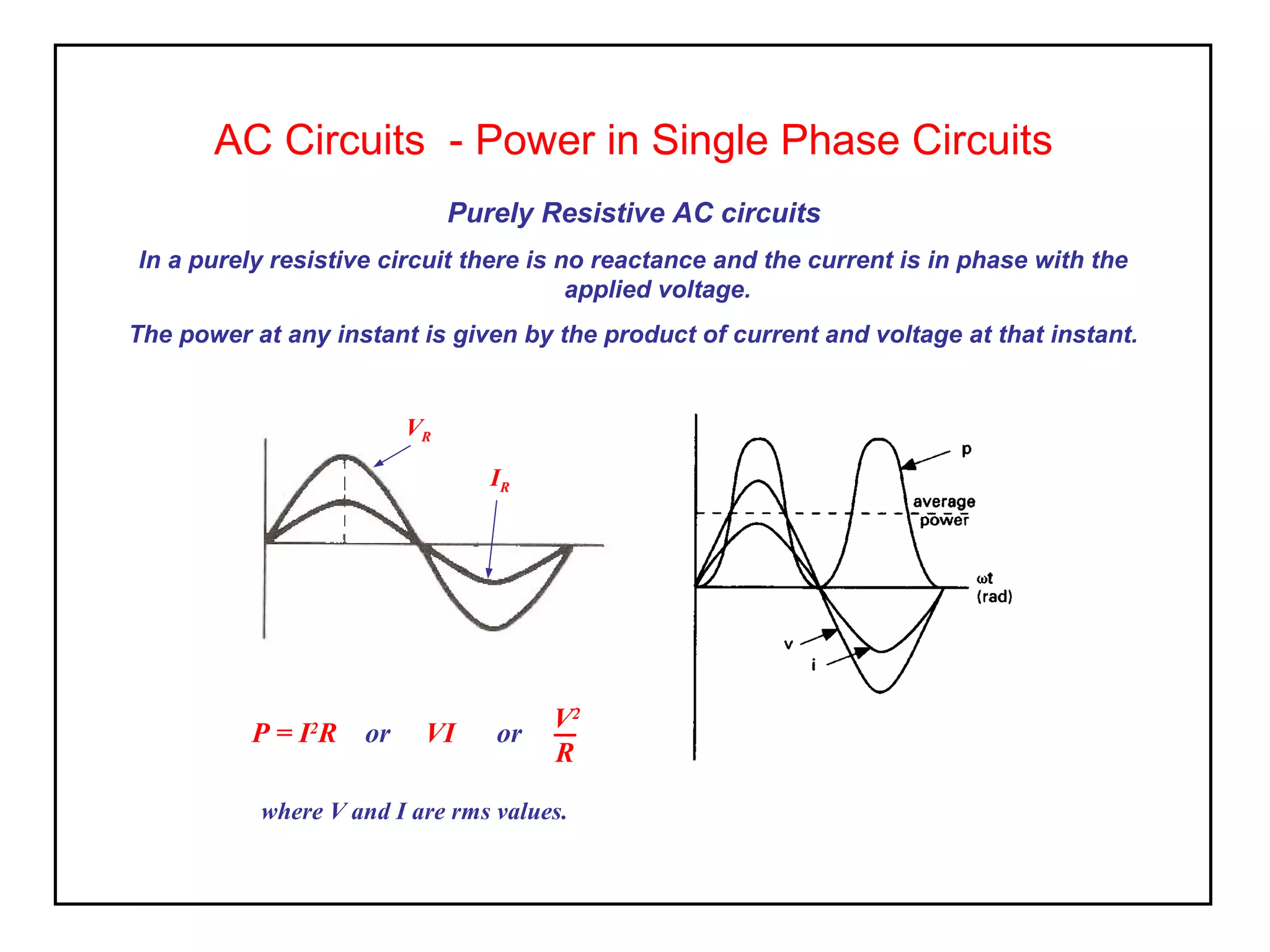
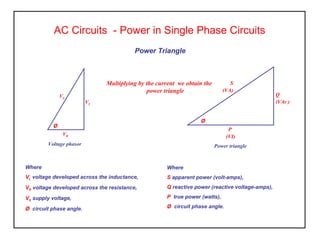
1) In purely resistive AC circuits, the current is in phase with the applied voltage. The power is given by the product of the rms current and voltage. 2) In purely inductive and capacitive circuits, the average power over a cycle is zero as the energy stored during one quarter cycle is returned during the next quarter cycle, so no net power is consumed. 3) Practical inductive circuits contain both inductance and resistance. The power consumed is given by the product of the current and voltage drop across the resistor, which are in phase. This power is known as the "true" power.

1. AC Circuits - Power in Single Phase Circuits
Purely Resistive AC circuits
In a purely resistive circuit there is no reactance and the current is in phase with the
applied voltage.
The power at any instant is given by the product of current and voltage at that instant.
IR
VR
where V and I are rms values.
P = I2
R or VI or
V2
R

2. AC Circuits - Power in Single Phase Circuits
Purely Inductive AC circuits
Average power dissipation over one cycle is zero since on the first quarter cycle the
magnetic field stores energy. During the next quarter cycle the field is collapsing
and the stored energy is returned back to the supply.
This sequence is repeated continuously on each half-cycle, thus no energy is
dissipated, so no power is consumed.

3. AC Circuits - Power in Single Phase Circuits
Purely Capacitive AC circuits
As with the inductor the power at any instant is the product of voltage and current at
that instant.
Average power dissipation over one cycle is zero since the energy stored in the electric
field in one quarter cycle is returned back to the supply during the next quarter
cycle.
This sequence is repeated continuously on each half-cycle, thus no energy is
dissipated, so no power is consumed.

4. AC Circuits - Power in Single Phase Circuits
Practical Inductive Circuits
In practice a pure inductor cannot exist since inductance is formed by the magnetising
effects of windings, these windings also have resistance.
A model for an inductor in an AC circuit is shown below with its phasor diagram,
Inductance and
resistance
L R
I
V
(AC)
VR
VL
Phasor Diagram
I
VR
VL
V
Ø
From the phasor diagram the only components that are in phase are I and VR .
The product of these two quantities is called the ‘true’ power and is the usable active
component of power.
P = VRI watts
but VR = Vcos Ø
P = VIcos Ø watts

5. Activity
1. A pure inductance of 150mH is connected to a 100V 50Hz. supply,
state the power dissipated and the phase angle between applied voltage and current.
2. A a coil of inductance of 500mH and resistance 80 ohms is connected to a 100V 50Hz.
Supply. Calculate a) the current flowing, b) the angle between applied voltage and
current and c) determine the power dissipated in the circuit.
AC Circuits - Power in Single Phase Circuits

6. Power Triangle
AC Circuits - Power in Single Phase Circuits
Where
VL voltage developed across the inductance,
VR voltage developed across the resistance,
VS supply voltage,
Ø circuit phase angle.
VR
VS
Voltage phasor
VL
Ø
P
(VI)
S
(VA)
Power triangle
Q
(VAr )
Ø
Multiplying by the current we obtain the
power triangle
Where
S apparent power (volt-amps),
Q reactive power (reactive voltage-amps),
P true power (watts),
Ø circuit phase angle.

7. Power Triangle
AC Circuits - Power in Single Phase Circuits
P
(VI)
S
(VA)
Q
(VAr )
Ø
‘S’ apparent power – this is the power as would be measured using the volt-meter /
ammeter method and has units of volt-amp (VA),
‘Q’ reactive power – this is the power used to develop the magnetic field in the coil
producing the inductance, it is also known as watt-less power and is a burden on
electrical systems. Its units are reactive voltage-amps (VAr ),
‘P’ true power – this is useful power developed and is measured in watts (W).
‘Ø’ circuit phase angle – From the power triangle it can be seen that this should be
small since the true power = S cos Ø. The greater this angle the higher are the
reactive power (higher losses).

8. Activity
1. A coil of inductance of 400mH and resistance 60 ohms is connected to a 100V 50Hz.
Supply. Calculate a) the current flowing, b) the angle between applied voltage and
current and c) determine the power dissipated in the circuit.
2. Repeat the above problem but using a coil with a reduced inductance of 200mH.
3. Repeat above with a coil of inductance 100mH.
4. In each case state the value of cosØ and the efficiency of the system
(true power/apparent power) and comment on your results.
AC Circuits - Power in Single Phase Circuits

9. Power in AC Circuits – What did we learn
• Power is only used in the resistive component.
• Reactive elements return power to the system.
• Apparent power is the product of measured voltage and current in a system.
• True power is less than the apparent power and dependant on the circuit
phase angle.
• Reactive power is wasted energy and a burden on the system.

10. Power in AC Circuits – What did we learn
• Power is only used in the resistive component.
• Reactive elements return power to the system.
• Apparent power is the product of measured voltage and current in a system.
• True power is less than the apparent power and dependant on the circuit
phase angle.
• Reactive power is wasted energy and a burden on the system.