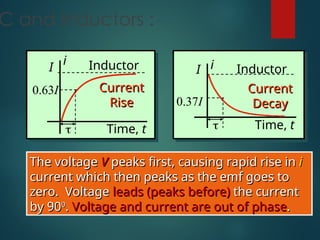
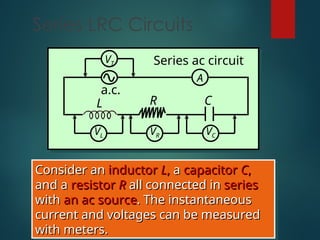
The document provides detailed explanations on alternating current (AC) circuits, including definitions of effective current and voltage, the behavior of inductors and capacitors, and the concepts of reactance and impedance. It discusses phase relationships in series circuits, resonance, and how to calculate power factors and total source voltage. Additionally, it outlines key equations and principles governing AC circuit behavior.

2. Roll No. Name
41. RATIYA RAJU
42. SATANI DARSHANA
43. SAVALIYA MILAN
44. SISARA GOVIND
45. VALGAMA HARDIK
46. VADHER DARSHAK
47. VADOLIYA MILAN
48. VALA GOPAL
49. SHINGADIYA SHYAM
50. KARUD LUKMAN

4. C Definitions :
One
One effective ampere
effective ampere is that ac current
is that ac current
for which the power is the same as for
for which the power is the same as for
one ampere of dc current.
one ampere of dc current.
One
One effective volt
effective volt is that ac voltage that
is that ac voltage that
gives an effective ampere through a
gives an effective ampere through a
resistance of one ohm.
resistance of one ohm.
Effective current: ieff = 0.707 imax
Effective voltage: Veff = 0.707 Vmax

5. Pure Resistance in AC Circuits
A
a.c. Source
R
V
Voltage and current are in phase, and Ohm’s
Voltage and current are in phase, and Ohm’s
law applies for effective currents and
law applies for effective currents and
voltages.
voltages.
Ohm’s law: Veff = ieffR
Vmax
i
imax
max
Voltage
Current

6. C and Inductors :
Time, t
I
i
Current
Current
Rise
Rise

0.63I
Inductor
The voltage
The voltage V
V peaks first, causing rapid rise in
peaks first, causing rapid rise in i
i
current which then peaks as the emf goes to
current which then peaks as the emf goes to
zero. Voltage
zero. Voltage leads (peaks before)
leads (peaks before) the current
the current
by 90
by 900
0
.
. Voltage and current are out of phase
Voltage and current are out of phase.
.
Time, t
I i
Current
Current
Decay
Decay

0.37I
Inductor

7. A Pure Inductor in AC Circuit
A
L
V
a.c.
Vmax
i
imax
max
Voltage
Current
The voltage peaks 90
The voltage peaks 900
0
before the current
before the current
peaks. One builds as the other falls and vice
peaks. One builds as the other falls and vice
versa.
versa.
The
The reactance
reactance may be defined as the
may be defined as the non-
non-
resistive
resistive opposition
opposition to the flow of ac current.
to the flow of ac current.

8. Inductive Reactance
A
L
V
a.c.
The
The back emf
back emf induced
induced
by a changing current
by a changing current
provides opposition to
provides opposition to
current, called
current, called
inductive
inductive reactance X
reactance XL
L.
.
Such losses are
Such losses are temporary
temporary, however, since the
, however, since the
current
current changes direction
changes direction, periodically re-
, periodically re-
supplying energy so that no net power is lost in
supplying energy so that no net power is lost in
one cycle.
one cycle.
Inductive reactance X
Inductive reactance XL
L is a function of both
is a function of both
the
the inductance
inductance and the
and the frequency
frequency of the ac
of the ac
current.
current.

9. Calculating Inductive Reactance
A
L
V
a.c.
Inductive Reactance:
2 Unit is the
L
X fL

 
Ohm's law: L L
V iX

The
The voltage
voltage reading
reading V
V in the above circuit at
in the above circuit at
the instant the
the instant the ac
ac current is
current is i
i can be found
can be found
from the
from the inductance
inductance in
in H
H and the
and the frequency
frequency
in
in Hz
Hz.
.
(2 )
L
V i fL

 Ohm’s law: VL = ieffXL

10. AC and Capacitance
Time, t
Qmax
q
Rise in
Rise in
Charge
Charge
Capacitor

0.63 I
Time, t
I
i
Current
Current
Decay
Decay
Capacitor

0.37 I
The voltage
The voltage V
V peaks ¼ of a cycle after the
peaks ¼ of a cycle after the
current
current i
i reaches its maximum. The voltage
reaches its maximum. The voltage
lags
lags the current.
the current. Current
Current i
i and V out of phase
and V out of phase.
.

11. A Pure Capacitor in AC Circuit
Vmax
i
imax
max
Voltage
Current
A V
a.c.
C
The voltage peaks 90
The voltage peaks 900
0
after
after the current peaks.
the current peaks.
One builds as the other falls and vice versa.
One builds as the other falls and vice versa.
The diminishing current
The diminishing current i
i builds charge on
builds charge on C
C
which increases the
which increases the back emf
back emf of
of V
VC.
C.

12. Capacitive Reactance
No
No net power
net power is lost in a complete cycle, even
is lost in a complete cycle, even
though the capacitor does provide non-resistive
though the capacitor does provide non-resistive
opposition (
opposition (reactance
reactance) to the flow of ac current.
) to the flow of ac current.
Capacitive reactance X
Capacitive reactance XC
C is affected by both the
is affected by both the
capacitance
capacitance and the
and the frequency
frequency of the ac
of the ac
current.
current.
A V
a.c.
C
Energy
Energy gains and
gains and
losses are also
losses are also
temporary
temporary for
for
capacitors due to the
capacitors due to the
constantly changing ac
constantly changing ac
current.
current.

13. Calculating capacitive Reactance
Capacitive Reactance:
1
Unit is the
2
C
X
fC

 
Ohm's law: VC C
iX

The
The voltage
voltage reading
reading V
V in the above circuit at
in the above circuit at
the instant the
the instant the ac
ac current is
current is i
i can be found
can be found
from the
from the inductance
inductance in
in F
F and the
and the frequency
frequency in
in
Hz
Hz.
.
2
L
i
V
fL


A V
a.c.
C
Ohm’s law: VC = ieffXC

14. Frequency and AC Circuits
f
f
R, X
R, X
1
2
C
X
fC


2
L
X fL


Resistance
Resistance R
R is constant and not affected by
is constant and not affected by
f.
f.
Inductive reactance X
Inductive reactance XL
L
varies directly with
varies directly with
frequency as expected
frequency as expected
since
since E
E  
i/
i/
t
t.
.
Capacitive reactance
Capacitive reactance X
XC
C
varies
varies inversely
inversely with
with f
f since
since
rapid ac allows little time for
rapid ac allows little time for
charge to build up on
charge to build up on
capacitors.
capacitors.
R
R
X
XL
L
X
XC
C

15. Series LRC Circuits
L
VR VC
C
R
a.c.
VL
VT
A
Series ac circuit
Consider an
Consider an inductor
inductor L
L,
, a
a capacitor
capacitor C
C,
,
and a
and a resistor
resistor R
R all connected in
all connected in series
series
with
with an ac source
an ac source. The instantaneous
. The instantaneous
current and voltages can be measured
current and voltages can be measured
with meters.
with meters.

16. Phase in a Series AC Circuit
The voltage
The voltage leads
leads current in an inductor and
current in an inductor and
lags
lags current in a capacitor.
current in a capacitor. In phase
In phase for
for
resistance
resistance R
R.
.

450
900
1350
1800
2700
3600
V V = Vmax sin 
VR
VC
VL
Rotating
Rotating phasor diagram
phasor diagram generates voltage
generates voltage
waves for each element
waves for each element R
R,
, L
L, and
, and C
C showing
showing
phase relations. Current
phase relations. Current i
i is always
is always in phase
in phase
with
with V
VR.
R.

17. Phasors and Voltage
At time t = 0, suppose we read
At time t = 0, suppose we read V
VL
L,
, V
VR
R and
and V
VC
C for an
for an
ac series circuit. What is the source voltage
ac series circuit. What is the source voltage V
VT
T?
?
We handle phase differences by finding the
We handle phase differences by finding the
vector sum
vector sum of these readings.
of these readings. V
VT
T =
= 
V
Vi
i.
. The
The
angle
angle 
 is the
is the phase angle
phase angle for the ac circuit.
for the ac circuit.

VR
VL - VC
V
VT
T
Source voltage
Source voltage
VR
VC
VL
Phasor
Phasor
Diagram
Diagram

18. Calculating Total Source Voltage

VR
VL - VC
V
VT
T
Source voltage
Source voltage Treating as vectors, we
Treating as vectors, we
find:
find:
2 2
( )
T R L C
V V V V
  
tan L C
R
V V
V



Now recall that:
Now recall that: V
VR
R = iR
= iR;
; V
VL
L = iX
= iXL
L;
; and
and V
VC
C = iV
= iVC
C
Substitution into the above voltage equation
Substitution into the above voltage equation
gives:
gives:
2 2
( )
T L C
V i R X X
  

19. Impedance in an AC Circuit

R
XL - XC
Z
Z
Impedance
Impedance 2 2
( )
T L C
V i R X X
  
Impedance
Impedance Z
Z is
is
defined:
defined:
2 2
( )
L C
Z R X X
  
Ohm’s law for ac current
Ohm’s law for ac current
and impedance:
and impedance:
or T
T
V
V iZ i
Z
 
The impedance is the combined opposition to ac
current consisting of both resistance and
reactance.

20. Resonant Frequency
Because
Because inductance
inductance causes the voltage to
causes the voltage to lead
lead
the current and
the current and capacitance
capacitance causes it to
causes it to lag
lag
the current, they tend to
the current, they tend to cancel
cancel each other
each other
out.
out.
Resonance
Resonance (Maximum
(Maximum
Power) occurs when X
Power) occurs when XL
L = X
= XC
C
R
XC
XL X
XL
L =
= X
XC
C
2 2
( )
L C
Z R X X R
   
1
2
2
fL
fC



1
2
r
f
LC


Resonant
Resonant f
fr
r
X
XL
L = X
= XC
C

21. Power in an AC Circuit
No power is consumed by inductance or
No power is consumed by inductance or
capacitance. Thus power is a function of the
capacitance. Thus power is a function of the
component of the impedance along
component of the impedance along
resistance:
resistance:
In terms of ac voltage:
In terms of ac voltage:
P = iV cos 
In terms of the resistance
In terms of the resistance
R:
R:
P = i2
R

R
XL - XC
Z
Z
Impedance
Impedance
P
P lost in
lost in R
R only
only
The fraction
The fraction Cos
Cos 

is known as the
is known as the power
power
factor.
factor.

22. Summary
Effective current: ieff = 0.707 imax
Effective voltage: Veff = 0.707 Vmax
Inductive Reactance:
2 Unit is the
L
X fL

 
Ohm's law: L L
V iX

Capacitive Reactance:
1
Unit is the
2
C
X
fC

 
Ohm's law: VC C
iX


23. Summary (Cont.)
2 2
( )
T R L C
V V V V
   tan L C
R
V V
V



2 2
( )
L C
Z R X X
  
or T
T
V
V iZ i
Z
 
tan L C
X X
R



1
2
r
f
LC



24. Summary (Cont.)
In terms of ac voltage:
In terms of ac voltage:
P = iV cos 
In terms of the resistance
In terms of the resistance
R:
R:
P = i2
R
Power in AC Circuits
Power in AC Circuits:
: