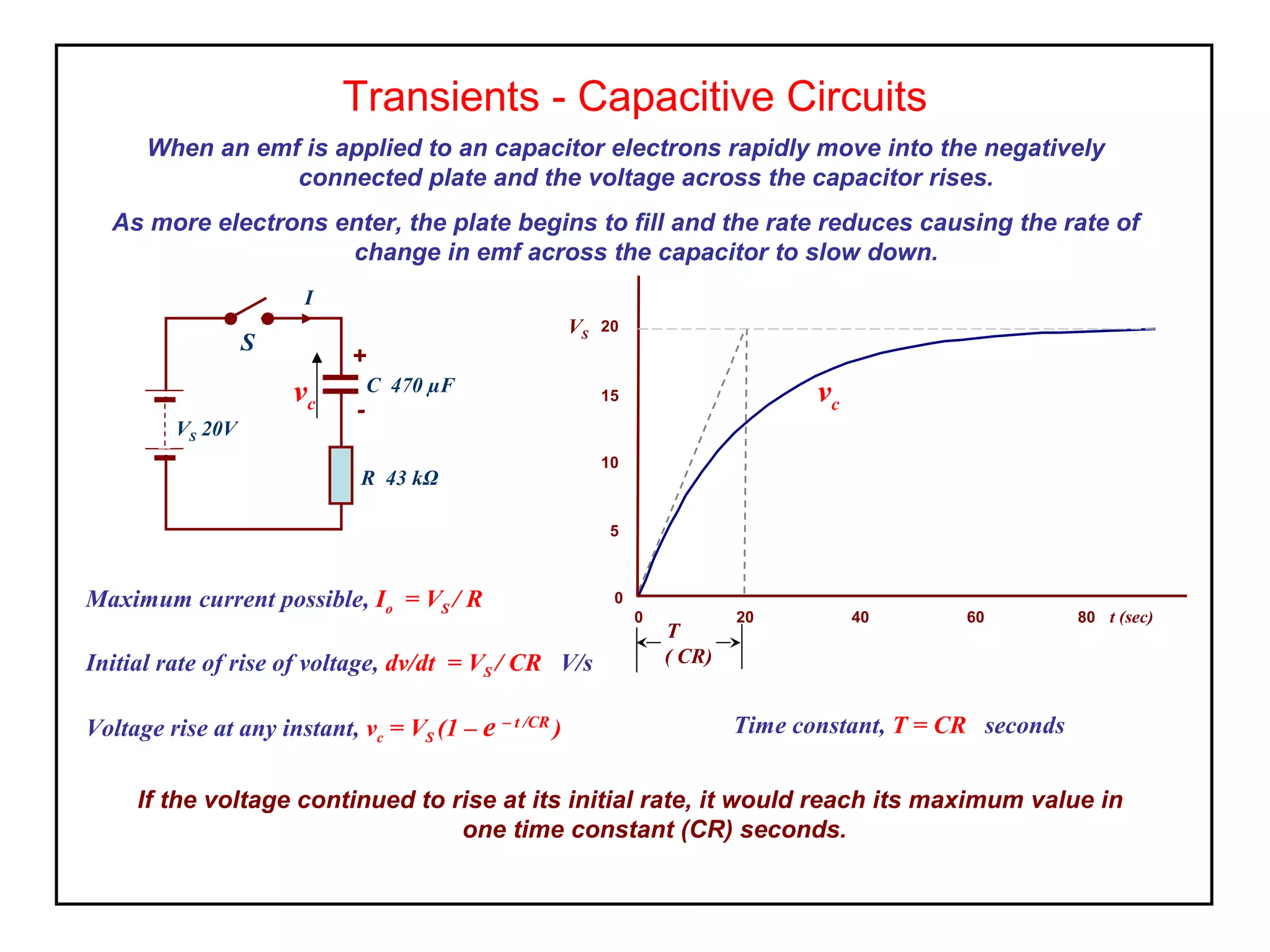
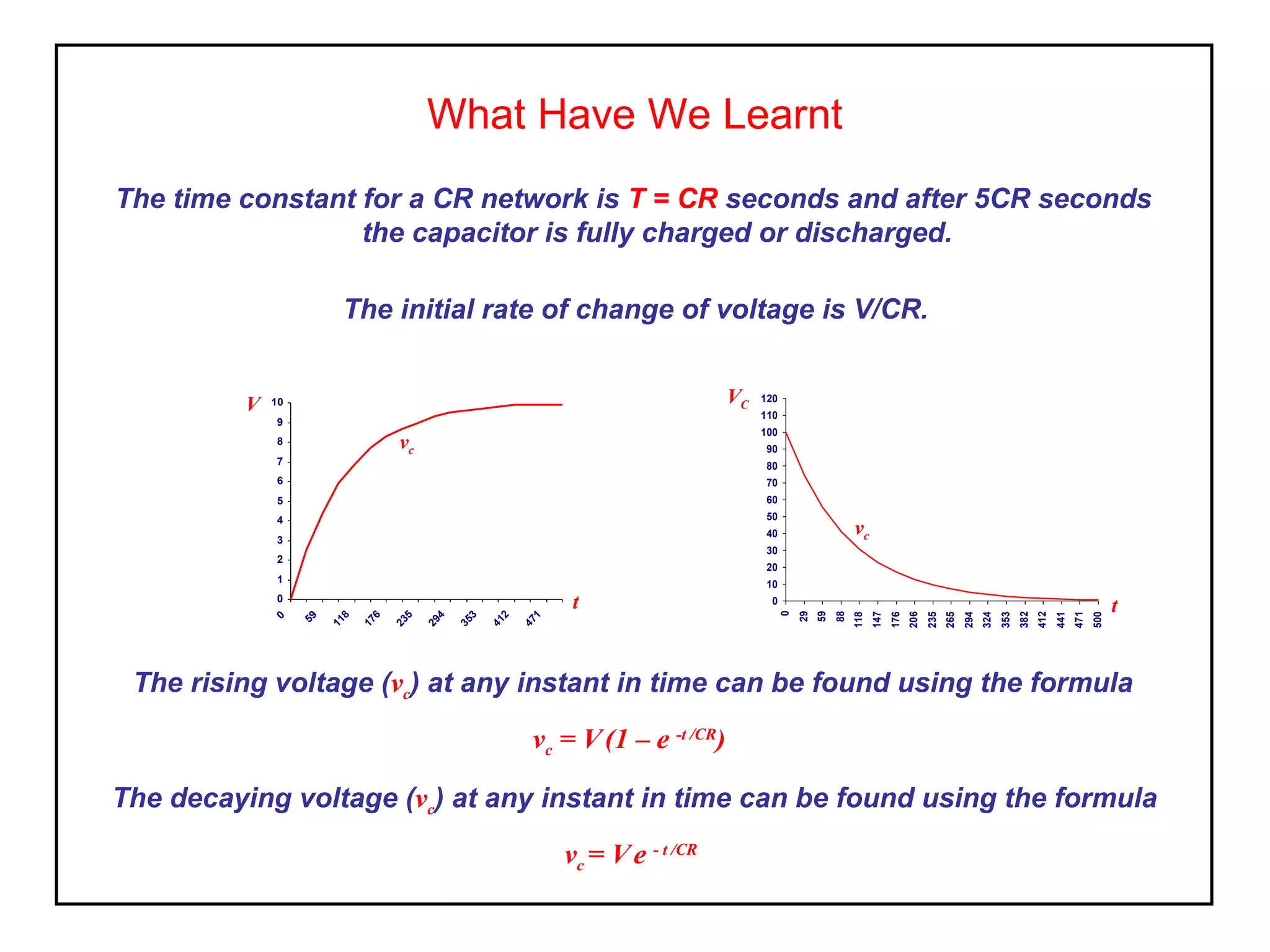
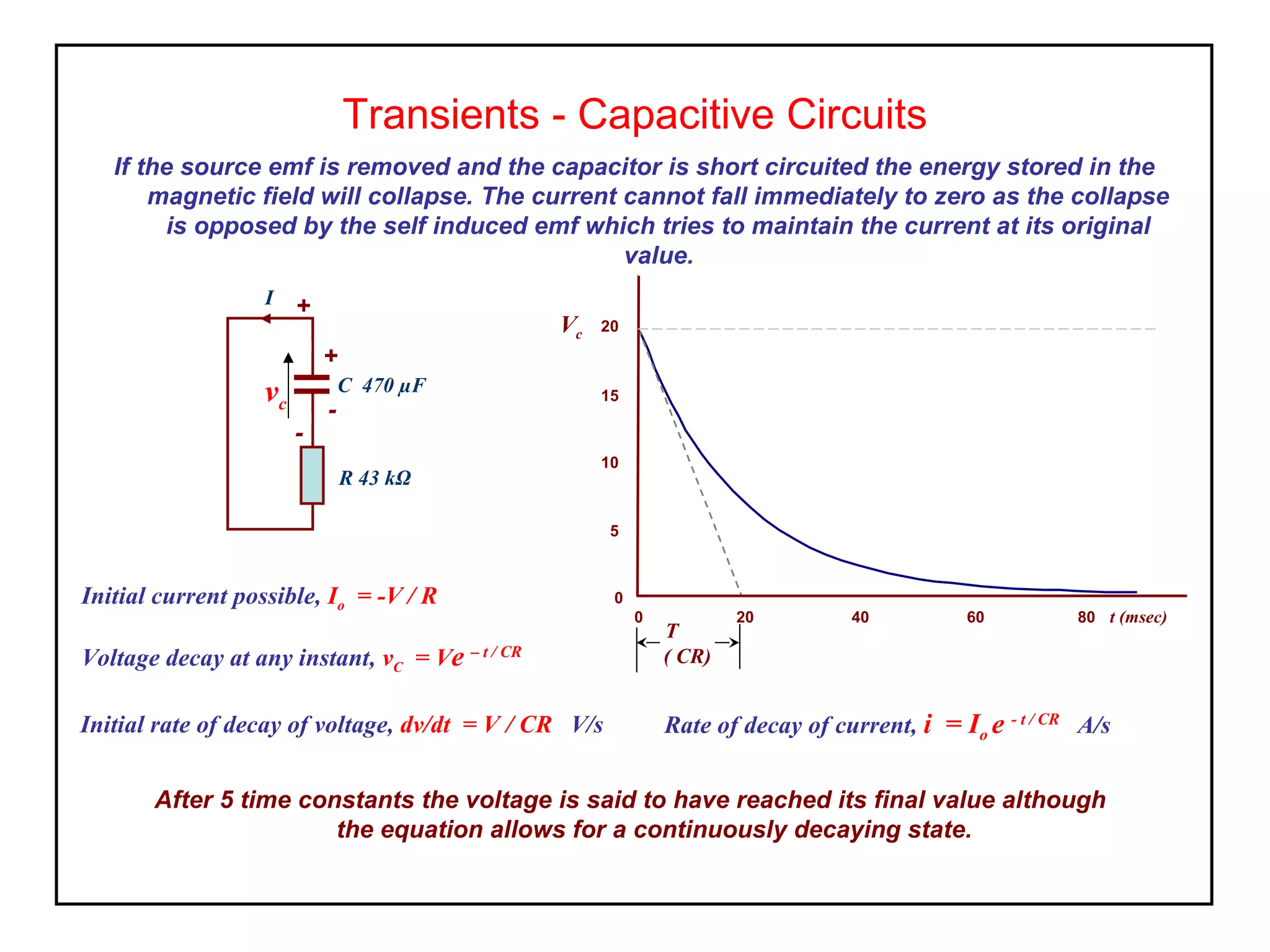
1. When a capacitor is charged by a voltage source through a resistor, the voltage across the capacitor rises exponentially as electrons move into the capacitor plates. The time it takes for the voltage to reach 63% of its final value is called the time constant and equals the product of the capacitor's capacitance and the resistor's resistance. 2. After being charged, if the voltage source is removed and the capacitor discharged through a short circuit, the stored energy will cause a current to flow which decays exponentially over the time constant as the electrons drain from the capacitor plates. 3. The voltage and current values at any time during the charging or discharging process can be calculated using equations that involve the time constant,

1. Transients - Capacitive Circuits
If the voltage continued to rise at its initial rate, it would reach its maximum value in
one time constant (CR) seconds.
Initial rate of rise of voltage, dv/dt = VS / CR V/s
Maximum current possible, Io = VS / R
Voltage rise at any instant, vc = VS (1 – e – t /CR
)
VS
T
( CR)
0 20 40 60 80 t (sec)
20
15
10
5
0
S
VS 20V
R 43 kΩ
I
C 470 µFvc -
+
vc
When an emf is applied to an capacitor electrons rapidly move into the negatively
connected plate and the voltage across the capacitor rises.
As more electrons enter, the plate begins to fill and the rate reduces causing the rate of
change in emf across the capacitor to slow down.
Time constant, T = CR seconds

2. If the source emf is removed and the capacitor is short circuited the energy stored in the
magnetic field will collapse. The current cannot fall immediately to zero as the collapse
is opposed by the self induced emf which tries to maintain the current at its original
value.
Transients - Capacitive Circuits
After 5 time constants the voltage is said to have reached its final value although
the equation allows for a continuously decaying state.
Initial current possible, Io = -V / R
Vc
T
( CR)
0 20 40 60 80 t (msec)
20
15
10
5
0
-
+
R 43 kΩ
I
C 470 µFvc -
+
Voltage decay at any instant, vC = Ve – t / CR
Rate of decay of current, i = Io e - t / CR
A/sInitial rate of decay of voltage, dv/dt = V / CR V/s

3. Transients – Capacitive Circuits
Activity
1. A 200µF capacitor is connected in series with a 10k resistor to a 20V dc
supply. Determine a) the time constant, b) the initial rate of increase in
voltage vC , c) the time to reach a fully charged state and d) the voltage
across the capacitor (vc) at t = CR seconds.
2. A 10µF capacitor is charged from a 100V supply through a series resistor of
500KΩ. Calculate the voltage across C for the following intervals after the
charge commences, (a) 2s, b) 5s and c) 10s.
3. A capacitance 470µF is connected to a 40V dc supply via a 10kΩ resistor
and allowed to become fully charged after which the supply is removed and
instantly replaced by a short circuit. Calculate a) the initial rate of decrease
of current and b) the voltage after CR seconds and 5CR seconds, c) the time
for the voltage to be reduced by 20%.

4. What Have We Learnt
The time constant for a CR network is T = CR seconds and after 5CR seconds
the capacitor is fully charged or discharged.
The initial rate of change of voltage is V/CR.
0
10
20
30
40
50
60
70
80
90
100
110
120
0
29
59
88
118
147
176
206
235
265
294
324
353
382
412
441
471
500
t
vc
VC
0
1
2
3
4
5
6
7
8
9
10
0
59
118
176
235
294
353
412
471
V
t
vc
The decaying voltage (vc) at any instant in time can be found using the formula
vc = Ve - t /CR
The rising voltage (vc) at any instant in time can be found using the formula
vc = V(1 – e -t /CR
)