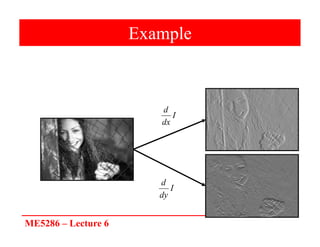
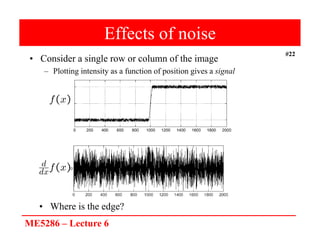
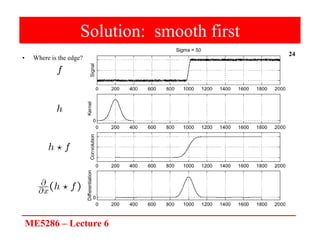
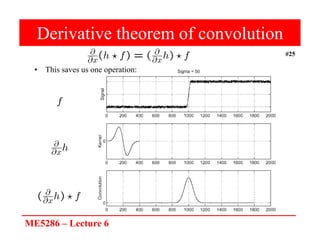
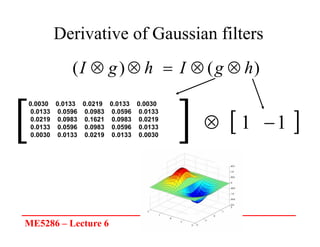
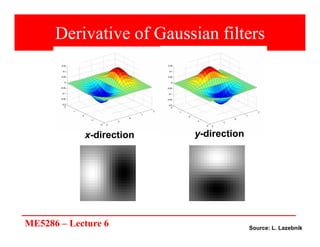
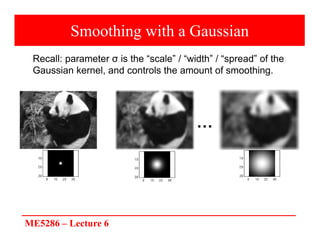
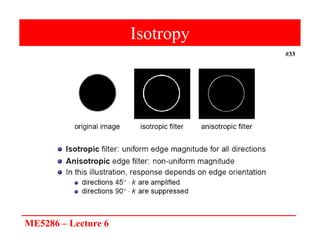
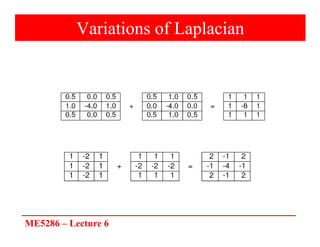
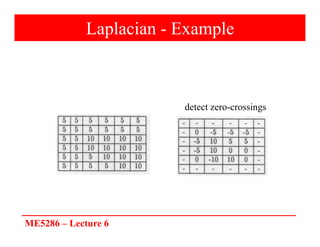
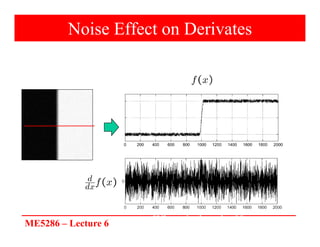
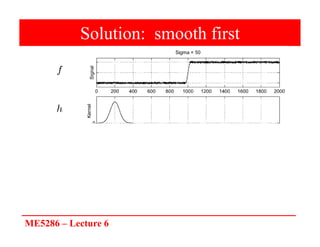
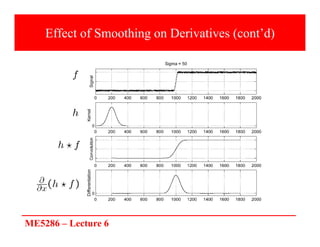
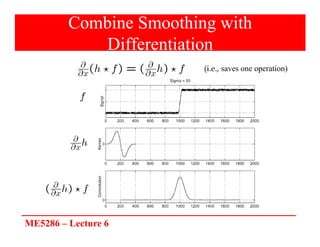
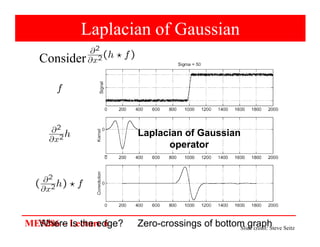
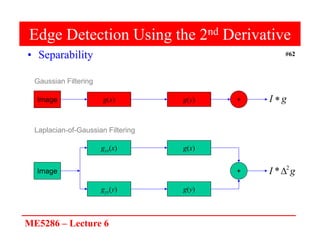
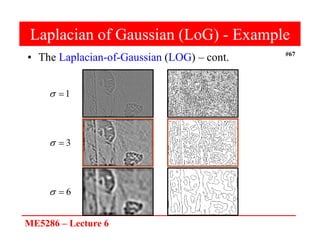
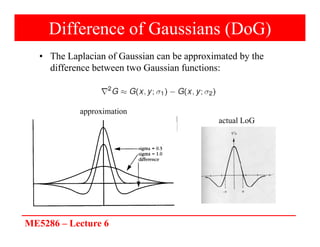
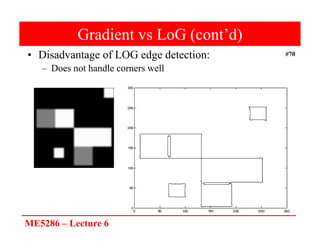
The document discusses edge detection in image processing, focusing on methods using first and second order derivatives, such as Sobel and Roberts operators, and the Laplacian of Gaussian. It emphasizes the importance of noise reduction techniques, optimal edge detection criteria, and the impact of variations in Gaussian smoothing on edge detection outcomes. Additionally, it covers practical issues such as noise suppression-localization tradeoffs and different thresholding strategies for effective edge identification.

1. ME5286 – Lecture 6
#1
Lecture 7:
Edge Detection
Saad J Bedros
sbedros@umn.edu

2. ME5286 – Lecture 6
#2
Review From Last Lecture
• Definition of an Edge
• First Order Derivative Approximation as
Edge Detector

3. ME5286 – Lecture 6
#3
This Lecture
• Examples of Edge Detection with first order
derivative approximation
• Edge Detection with Second order
derivative
• Combining Smoothing and Edge Detection
with Laplacian of Gaussian

4. ME5286 – Lecture 6
#4
Summary: Edge Definition
• Edge is a boundary between two regions with relatively distinct gray level
properties.
• Edges are pixels where the brightness function changes abruptly.
• Edge detectors are a collection of very important local image pre-
processing methods used to locate (sharp) changes in the intensity function.

5. ME5286 – Lecture 6
Criteria for Optimal Edge Detection
• (1) Good detection
– Minimize the probability of false positives (i.e., spurious edges).
– Minimize the probability of false negatives (i.e., missing real
edges).
• (2) Good localization
– Detected edges must be as close as possible to the true edges.
• (3) Single response
– Minimize the number of local maxima around the true edge.

6. ME5286 – Lecture 6
Edge Detection Using Derivatives
• Often, points that lie on an edge
are detected by:
(1) Detecting the local maxima or
minima of the first derivative.
(2) Detecting the zero-crossings
of the second derivative.
2nd derivative
1st derivative

7. ME5286 – Lecture 6
Edge Detection Using First Derivative
sensitive to vertical edges!
sensitive to horizontal edges!

8. ME5286 – Lecture 6
• We can implement and using the following masks:
(x+1/2,y)
(x,y+1/2)
*
*
good approximation
at (x+1/2,y)
good approximation
at (x,y+1/2)
Edge Detection Using First Derivative

9. ME5286 – Lecture 6
Approximation of First Derivative ( Gradient )
• Consider the arrangement of pixels about the pixel (i, j):
• The partial derivatives can be computed by:
• The constant c implies the emphasis given to pixels closer to
the center of the mask.
3 x 3 neighborhood:

10. ME5286 – Lecture 6
Prewitt Operator
• the Prewitt operator:

11. ME5286 – Lecture 6
Sobel Operator
• the Sobel operator:

12. ME5286 – Lecture 6
#12
Robert Edge Detection
• The Roberts edge detector
• This approximation can be implemented by the following masks:
Note: Mx and My are approximations at (i + 1/2, j
+ 1/2)

13. ME5286 – Lecture 6
#13
Roberts Edge Detector
There are two forms of the Roberts Edge Detector:
 The second form of the equation is often used in practice
due to its computational efficiency

14. ME5286 – Lecture 6
#14
Roberts Edge Detector
• A simple approximation to the first
derivative
• Marks edge points only; it does not return
any information about the edge
orientation
• Simplest of the edge detection operators
and will work best with binary images

15. ME5286 – Lecture 6
Example
I
dx
d
I
dy
d

16. ME5286 – Lecture 6
#16
Edge Detection Using Derivative
• Image derivatives:
 
1
1
* 
 I
Ix







1
1
*
I
Iy
Image I

17. ME5286 – Lecture 6
#17
Edge Detection Using the Gradient
• Example – cont.:
2
2
















 I
dy
d
I
dx
d

18. ME5286 – Lecture 6
#18
Edge Detection Using the Gradient
• Example – cont.:
100


 Threshold

19. ME5286 – Lecture 6
#19
Derivatives and Noise
• Derivatives are strongly affected by noise
– obvious reason: image noise results in pixels that look very
different from their neighbors
– The larger the noise - the stronger the response
• What is to be done?
– Neighboring pixels look alike
– Pixel along an edge look alike
– Image smoothing should help
– Force pixels different to their neighbors (possibly noise) to
look like neighbors

20. ME5286 – Lecture 6
#20
Derivatives and Noise
Increasing noise
– Need to perform image smoothing as a preliminary step
– Generally – use Gaussian smoothing

21. ME5286 – Lecture 6
#21
Edge Detection & Image Noise
i.i.d
)
,
0
(
~
)
(
)
(
)
(
ˆ
)
( 
N
x
N
x
N
x
I
x
I 



 


 



 


 

)
(
)
(
'
ˆ
))
1
(
-
)
1
(
(
))
1
(
ˆ
)
1
(
ˆ
(
))
1
(
)
1
(
ˆ
(
-
)
1
(
)
1
(
ˆ
)
(
'
x
N
x
I d
x
N
x
N
x
I
x
I
x
N
x
I
x
N
x
I
x
I
















))
(
( x
N
E d 0
Taking differences:
Output noise:

))
(
(
2
x
N
E d






 )
)
1
(
)
1
(
2
)
1
(
)
1
(
( 2
2
x
N
x
N
x
N
x
N
E
2
2
2
2
0 

 



Increases noise !!

22. ME5286 – Lecture 6
#22
Effects of noise
• Consider a single row or column of the image
– Plotting intensity as a function of position gives a signal
• Where is the edge?

23. ME5286 – Lecture 6
#23
Noise in Edge Detection
• Practical issues:
– Differential masks act as high-pass filters – tend to amplify noise.
– Reduce the effects of noise - first smooth with a low-pass filter.
1)The noise suppression-localization tradeoff
– a larger filter reduces noise, but worsens localization (i.e., it
adds uncertainty to the location of the edge) and vice-versa.

24. ME5286 – Lecture 6
#24
• Where is the edge?
Solution: smooth first

25. ME5286 – Lecture 6
#25
Derivative theorem of convolution
• This saves us one operation:

26. ME5286 – Lecture 6
 
1
1 

0.0030 0.0133 0.0219 0.0133 0.0030
0.0133 0.0596 0.0983 0.0596 0.0133
0.0219 0.0983 0.1621 0.0983 0.0219
0.0133 0.0596 0.0983 0.0596 0.0133
0.0030 0.0133 0.0219 0.0133 0.0030
)
(
)
( h
g
I
h
g
I 




Derivative of Gaussian filters

27. ME5286 – Lecture 6
Derivative of Gaussian filters
x-direction y-direction
Source: L. Lazebnik

28. ME5286 – Lecture 6
Smoothing with a Gaussian
Recall: parameter σ is the “scale” / “width” / “spread” of the
Gaussian kernel, and controls the amount of smoothing.
…

29. ME5286 – Lecture 6
Effect of σ on derivatives
The apparent structures differ depending on
Gaussian’s scale parameter.
Larger values: larger scale edges detected
Smaller values: finer features detected
σ = 1 pixel σ = 3 pixels

30. ME5286 – Lecture 6
Edge Detection Steps Using Gradient
(i.e., sqrt is costly!)

31. ME5286 – Lecture 6
Edge Direction Implementation
• Typically quantize the gradient orientation to a
fixed number of orientations
• You can identify the edges based on
magnitude and direction
How Many Directions or Levels ?

32. ME5286 – Lecture 6
#32

33. ME5286 – Lecture 6
Isotropy
#33

34. ME5286 – Lecture 6
Isotropic property of gradient
magnitude
• The magnitude of the gradient detects edges in all directions.
2
2
d d
I I
dx dy
 
 
    
 
   
I
dx
d I
dy
d

35. ME5286 – Lecture 6
#35
Edge Detection Using the Gradient
• Isotropic property of gradient magnitude:
– The magnitude of gradient is an isotropic operator (it detects
edges in any direction !!)

36. ME5286 – Lecture 6
Anisotropic Filtering
(i.e., edge preserving smoothing)
• Symmetric Gaussian smoothing tends to blur out edges
rather aggressively.
• An “oriented” smoothing operator would work better:
(i) Smooth aggressively perpendicular to the gradient
(ii) Smooth little along the gradient

37. ME5286 – Lecture 6
Anisotropic filtering - Example
result using
anisotropic filtering

38. ME5286 – Lecture 6
#38

39. ME5286 – Lecture 6
#39
Edge Detection Using the 2nd Derivative
• Edge points can be detected by finding the zero-
crossings of the second derivative.
• There are two approaches that uses the second
derivative to identify the edge presence
• Smoothing then apply Gradient
• Combine smoothing and Gradient Opertations

40. ME5286 – Lecture 6
Edge Detection Using Second
Derivative
• Approximate finding maxima/minima of
gradient magnitude by finding places
where:
• Can’t always find discrete pixels where the
second derivative is zero – look for zero-
crossing instead.

41. ME5286 – Lecture 6
#41
Edge Detection Using Second Derivative
• Computing the 2nd derivative:
– This approximation is centered about x + 1
– By replacing x + 1 by x we obtain:

42. ME5286 – Lecture 6
Image Derivatives
• 1st order
• 2nd order

43. ME5286 – Lecture 6
Edge Detection Using Second Derivative (cont’d)

44. ME5286 – Lecture 6
#44
Edge Detection Using Second Derivative (cont’d)
• Computing the 2nd derivative – cont.
– Examples using the edge models:

45. ME5286 – Lecture 6
Edge Detection Using Second Derivative (cont’d)
(upward) step edge
(downward) step edge
ramp edge
roof edge

46. ME5286 – Lecture 6
Edge Detection Using Second Derivative (cont’d)
• Four cases of zero-crossings:
{+,-}, {+,0,-},{-,+}, {-,0,+}
• Slope of zero-crossing {a, -b} is: |a+b|.
• To detect “strong” zero-crossing, threshold
the slope.

47. ME5286 – Lecture 6
Second Derivative in 2D: Laplacian

48. ME5286 – Lecture 6
Second Derivative in 2D: Laplacian

49. ME5286 – Lecture 6
Variations of Laplacian

50. ME5286 – Lecture 6
Laplacian - Example
detect zero-crossings

51. ME5286 – Lecture 6
Properties of Laplacian
• It is cheaper to implement than the gradient
(i.e., one mask only).
• It does not provide information about edge
direction.
• It is more sensitive to noise (i.e.,
differentiates twice).
• It is an isotropic operator ( equal weights in
all directions )

52. ME5286 – Lecture 6
Noise Effect on Derivates
Where is the edge??

53. ME5286 – Lecture 6
Solution: smooth first

54. ME5286 – Lecture 6
Effect of Smoothing on Derivatives (cont’d)

55. ME5286 – Lecture 6
Combine Smoothing with
Differentiation
(i.e., saves one operation)

56. ME5286 – Lecture 6
Laplacian of Gaussian
Consider
Laplacian of Gaussian
operator
Where is the edge? Zero-crossings of bottom graph
Slide credit: Steve Seitz

57. ME5286 – Lecture 6
2D edge detection filters
• is the Laplacian operator:
Laplacian of Gaussian
Gaussian derivative of Gaussian
Slide credit: Steve Seitz

58. ME5286 – Lecture 6
Laplacian of Gaussian (LoG)
(Marr-Hildreth operator)
• To reduce the noise effect, the image is first smoothed.
• When the filter chosen is a Gaussian, we call it the LoG
edge detector.
• It can be shown that:
σ controls smoothing
2σ2
(inverted
LoG)

59. ME5286 – Lecture 6
Laplacian of Gaussian (LoG)
(Marr-Hildreth operator)
• The 2-D Laplacian of Gaussian (LoG) function centered on zero and with
Gaussian standard deviation has the form:
where σ is the standard deviation
• The amount of smoothing can be controlled by varying the value of the
standard deviation.

60. ME5286 – Lecture 6
Laplacian of Gaussian (LoG) -
Example
filtering zero-crossings
(inverted LoG)
(inverted LoG)

61. ME5286 – Lecture 6
Decomposition of LoG
• It can be shown than LoG can be written as
follows:
• 2D LoG convolution can be implemented
using 4, 1D convolutions.
2
( , )
g x y

2
( , )* ( , )
g x y I x y


62. ME5286 – Lecture 6
#62
Edge Detection Using the 2nd Derivative
• Separability
Image
gxx(x) g(x)
gyy(y) g(y)
+ g
I 2
*
Image g(x) g(y) + g
I 
Gaussian Filtering
Laplacian-of-Gaussian Filtering

63. ME5286 – Lecture 6
#63
Edge Detection Using the 2nd Derivative
• Separability
– Gaussian:
• A 2-D Gaussian can be separated into two 1-D Gaussians
• Perform 2 convolutions with 1-D Gaussians
)
,
(
*
)
,
(
)
,
( y
x
g
y
x
I
y
x
h 
  )
(
*
)
(
*
)
,
(
)
,
( 2
1 y
g
x
g
y
x
I
y
x
h 
n2 multiplications per pixel
2n multiplications per pixel
 
011
.
13
.
6
.
1
6
.
13
.
011
.
1 
g























011
.
13
.
6
.
1
6
.
13
.
011
.
2
g

64. ME5286 – Lecture 6
Decomposition of LoG (cont’d)
Steps

65. ME5286 – Lecture 6
#65
Edge Detection Using LOG
• Marr-Hildteth (LOG) Algorithm:
– Compute LoG
• Use one 2D filter:
• Use four 1D filters:
– Find zero-crossings from each row and column
– Find slope of zero-crossings
– Apply threshold to slope and mark edges
)
,
(
2
y
x
g

)
(
),
(
),
(
),
( y
g
y
g
x
g
x
g yy
xx

66. ME5286 – Lecture 6
#66
Laplacian of Gaussian (LoG) - Example
• The Laplacian-of-Gaussian (LOG) – cont.
 
G
I 2
* 
I
)
(
*
I
of
crossings
Zero 2
G


67. ME5286 – Lecture 6
#67
Laplacian of Gaussian (LoG) - Example
• The Laplacian-of-Gaussian (LOG) – cont.
1


6


3



68. ME5286 – Lecture 6
Difference of Gaussians (DoG)
• The Laplacian of Gaussian can be approximated by the
difference between two Gaussian functions:
approximation
actual LoG

69. ME5286 – Lecture 6
Difference of Gaussians (DoG) (cont’d)
(a) (b) (b)‐(a)

70. ME5286 – Lecture 6
#70
Gradient vs LoG (cont’d)
• Disadvantage of LOG edge detection:
– Does not handle corners well

71. ME5286 – Lecture 6
Gradient vs LoG
• Gradient works well when the image contains sharp
intensity transitions and low noise.
• Zero-crossings of LOG offer better localization, especially
when the edges are not very sharp.
step edge
ramp edge

72. ME5286 – Lecture 6
Practical Issues
• Noise suppression-localization tradeoff.
– Smoothing depends on mask size (e.g., depends
on σ for Gaussian filters).
– Larger mask sizes reduce noise, but worsen
localization (i.e., add uncertainty to the location
of the edge) and vice versa.
larger mask
smaller mask

73. ME5286 – Lecture 6
Choice of Threshold
• Trade off of threshold value.
gradient magnitude
low threshold high threshold

74. ME5286 – Lecture 6
Standard thresholding
• Standard thresholding:
- Can only select “strong” edges.
- Does not guarantee “continuity”.
gradient magnitude low threshold high threshold

75. ME5286 – Lecture 6
Hysteresis thresholding
• Hysteresis thresholding uses two thresholds:
• For “maybe” edges, decide on the edge if neighboring
pixel is a strong edge.
- low threshold tl
- high threshold th (usually, th = 2tl)
tl
tl
th
th

76. ME5286 – Lecture 6
Hysteresis Thresholding Example
#76

77. ME5286 – Lecture 6
#77
Edge Detection Review
• Edge detection operators are based on the idea that
edge information in an image is found by looking
at the relationship a pixel has with its neighbors
• If a pixel's gray level value is similar to those
around it, there is probably not an edge at that
point

78. ME5286 – Lecture 6
#78
Edge Detection Review
• Edge detection operators are often
implemented with convolution masks and
most are based on discrete approximations
to differential operators
• Differential operations measure the rate of
change in a function, in this case, the image
brightness function

79. ME5286 – Lecture 6
#79
Edge Detection Review
• Preprocessing of image is required to eliminate or
at least minimize noise effects
• There is tradeoff between sensitivity and accuracy
in edge detection
• The parameters that we can set so that edge
detector is sensitive include the size of the edge
detection mask and the value of the gray level
threshold
• A larger mask or a higher gray level threshold will
tend to reduce noise effects, but may result in a
loss of valid edge points