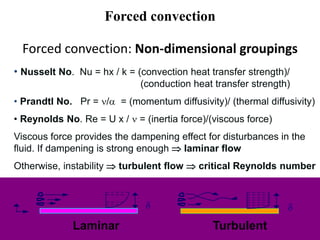
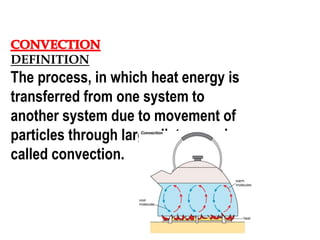
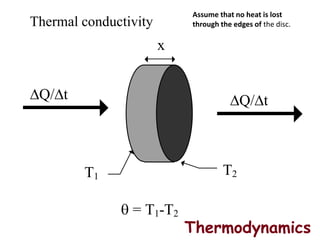
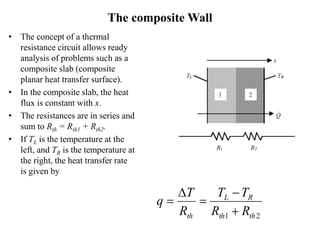
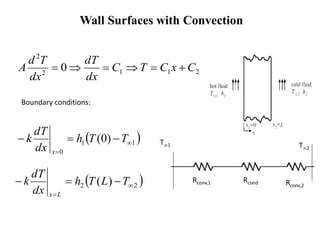
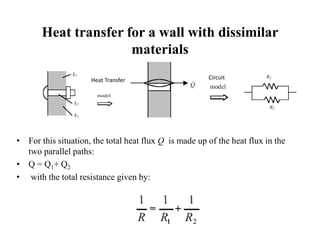
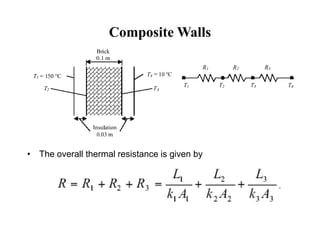
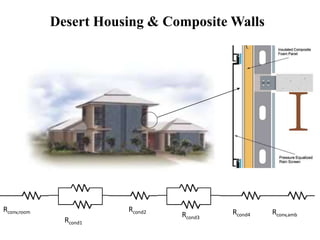
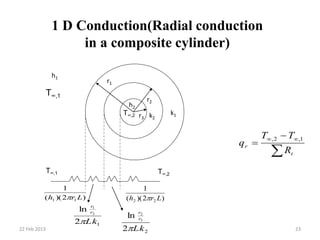
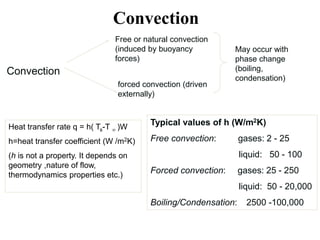
This document provides information on different modes of heat transfer including conduction, convection and radiation. It defines conduction as the transfer of heat through direct contact of particles over large distances. Convection is defined as the transfer of heat from one place to another inside a system through fluid motion, requiring a material medium. Radiation is defined as the transfer of heat in the form of electromagnetic waves with no need for a material medium. The document also discusses various concepts related to these modes of heat transfer such as Fourier's law of conduction, heat transfer coefficients, Nusselt number, Prandtl number and Reynolds number.

1. G.H Patel collage of engineering and
technology
NAME- Ravi Jethva -150110109016
Kevin Dias -150110109017
Khirsariya Vasu - 150110109018
Kothadia Yash - 150110109019
Lalkiya Abhishek -150110109020
1
Applied thermal and hydraulic engineering

2. HEAT
TRANSFER

3. Modes
Conduction
Convection
Radiation

4. Conduction

6. DEFINITION
The process, in which heat energy is
transferred from one system to
another system due to movement of
particles through large distances, is
called convection.

7. EXPLANATION
In fluids (liquids or gases) heat
transfer from one place to
another inside a system takes
place through convection. This
mode of transfer of heat
requires a material medium.
The molecules take heat the
heat energy and their kinetic
energy increases and they
carry heat through large
distances.

8. •VENTILATORS: Ventilators are provided in the walls
of a room near the ceiling, which help to keep the room
temperature moderate by continuous circulation of air.
The air inside the room gets impure and heated due to
our breathing. This hot air rises up and passes out
through ventilators, thus allowing space for currents of
fresh air from outside windows or doors.

9. As air warmed at the Equator rises towards the poles,
the rotation of the Earth causes it to deflect and flow
back towards the Equator. In the northern hemisphere,
the winds blow from the east to the west, while they
blow in the opposite direction in the southern
hemisphere. These winds tend to be much stronger
over open water than they are across land, which has
made them ideal for sailors.

10. LAND BREEZES AND SEA BREEZES:
Land is better conductor of heat than water. hence in day time,
the land gets hotter than in the sea. The air above the land
becomes warm and rises up being lighter and some what cold
air above sea surface moves towards the sea shore. This is
known as sea breeze.
During night land becomes cooler than water and so warm air over the
water in sea rises up. The air on the land near the sea shore begins to
move towards sea side and is called land breeze

11. RADIATION
DEFINITION
“The process in which heat energy travels from one
system to another in the form of electromagnetic
waves with no need of material medium is called
Radiation.”
EXPLAINATION: In radiation heat travels from
one system to another in the form of
electromagnetic radiations (photons). Thus no
medium is required for this mode of transfer of
heat.

12. Heat from the sun reaches earth by radiation

13. • A rate equation that allows determination of the conduction heat flux
from knowledge of the temperature distribution in a medium
Fourier’s Law
• Its most general (vector) form for multidimensional conduction is:
q k T
 
   
Implications:
– Heat transfer is in the direction of decreasing temperature
(basis for minus sign).
– Direction of heat transfer is perpendicular to lines of constant
temperature (isotherms).
– Heat flux vector may be resolved into orthogonal components.
– Fourier’s Law serves to define the thermal conductivity of the
medium /k q T
  
   
 

15. Thermodynamics
x
Q/t Q/t
T1 T2
 = T1-T2
Assume that no heat is lost
through the edges of the disc.Thermal conductivity

16. Thermodynamic
x
Q/t Q/t
T1 T2
 = T1-T2
For a uniform rod the rate of flow of heat through a
conductor ( Q/  t) is proportional to
•the cross sectional area (A) of the conductor
•the temperature gradient (  q/  x)
The constant of proportionality, k, is the thermal conductivity BUT note that heat
flows down a temperature gradient so we also introduce a negative sign to account
for this and obtain:




Q
T
kA
x
 

Thermal conductivity

17. Thermodynamics
k depends on the material and is called the thermal conductivity.
Rearranging in terms of k we can evaluate the units of k:
k
Q
t A
x
 

 


 Wm-2
K-1
m  Wm-1
K-1
So k is defined as the rate of flow of
heat through unit area of cross
section of 1m of material when the
temperature difference between the
surfaces is 1K.
Thermal conductivity

18. The composite Wall
• The concept of a thermal
resistance circuit allows ready
analysis of problems such as a
composite slab (composite
planar heat transfer surface).
• In the composite slab, the heat
flux is constant with x.
• The resistances are in series and
sum to Rth = Rth1 + Rth2.
• If TL is the temperature at the
left, and TR is the temperature at
the right, the heat transfer rate
is given by
21 thth
RL
th RR
TT
R
T
q






19. Wall Surfaces with Convection
2112
2
0 CxCTC
dx
dT
dx
Td
A 
Boundary conditions:
 11
0
)0( 

 TTh
dx
dT
k
x
 22 )( 

 TLTh
dx
dT
k
Lx
Rconv,1 Rcond Rconv,2
T1 T2

20. Heat transfer for a wall with dissimilar
materials
• For this situation, the total heat flux Q is made up of the heat flux in the
two parallel paths:
• Q = Q1+ Q2
• with the total resistance given by:
Heat Transfer Circuit

21. Composite Walls
• The overall thermal resistance is given by

22. Desert Housing & Composite Walls
Rconv,room Rconv,amb
Rcond1
Rcond2
Rcond3
Rcond4

23. 1 D Conduction(Radial conduction
in a composite cylinder)
22 Feb 2013 23
h1
T∞,1
k1
r1
r2
k2
T∞,2 r3
h2
T∞,1 T∞,2
)2)((
1
11 Lrh  )2)((
1
22 Lrh 
12
ln 2
1
Lk
r
r

22
ln 3
2
Lk
r
r


 

t
r
R
TT
q
1,2,

24. Logarithmic Mean area for hollow cylinder
• Convenient to have an expression for heat
flow through hollow cylinder of the same form
as that of for a plane wall.
• Then cylinder thickness will be equal to wall
thickness,
• Area will be equal to Am
22 Feb 2013 24

25. Logarithmic Mean area for
hollow cylinder
22 Feb 2013 25
22 1 1
22 1 1
ln( 2 / 1) ( 2 1)
2
ln( 2 / 1) ( 2 1)
ln( 2 / 1) ( 2 1) 2
2
2 ( 2 1) 2 ( 2 1)
ln( 2 / 1) ln(2 2 / 2 1)
2 1
ln( 2 / 1)
cylinder wall
m
m
m
m m
m
TT T T
Q and Q
r r r r
KL KA
TT T T r r r r
r r r r KL KA
KL KA
L r r L r r
A A
r r Lr Lr
A A
A
A A



 
 

 
 

  
 

 
 


26. Convection
• Heat transfer in the presence of a fluid motion on a solid surface
•Various mechanisms at play in the fluid:
- advection  physical transport of the fluid
- diffusion  conduction in the fluid
- generation  due to fluid friction
•But fluid directly in contact with the wall does not move relative to it; hence
direct heat transport to the fluid is by conduction in the fluid only.
T(y)q”
y y
U  T
Ts
u(y)
U 
 






 TTh
y
T
kq s
y
fconv
0
But depends on the whole fluid motion, and both fluid flow
and heat transfer equations are needed
0





y
y
T
T(y)
y TU 
Ts

27. Convection
Free or natural convection
(induced by buoyancy
forces)
forced convection (driven
externally)
May occur with
phase change
(boiling,
condensation)
Convection
Typical values of h (W/m2K)
Free convection: gases: 2 - 25
liquid: 50 - 100
Forced convection: gases: 25 - 250
liquid: 50 - 20,000
Boiling/Condensation: 2500 -100,000
Heat transfer rate q = h( Ts-T  )W
h=heat transfer coefficient (W /m2K)
(h is not a property. It depends on
geometry ,nature of flow,
thermodynamics properties etc.)

28. T(y)q”
y
U  T
Ts
u(y)
U 
Convection rate equation
Main purpose of convective heat
transfer analysis is to determine:
• flow field
• temperature field in fluid
• heat transfer coefficient, h
q’’=heat flux = h(Ts - T)
q’’ = -k(T/ y)y=0
Hence, h = [-k(T/ y)y=0] / (Ts - T)
The expression shows that in order to determine h, we
must first determine the temperature distribution in the
thin fluid layer that coats the wall.

29. • Nusselt No. Nu = hx / k = (convection heat transfer strength)/
(conduction heat transfer strength)
• Prandtl No. Pr = / = (momentum diffusivity)/ (thermal diffusivity)
• Reynolds No. Re = U x /  = (inertia force)/(viscous force)
Viscous force provides the dampening effect for disturbances in the
fluid. If dampening is strong enough  laminar flow
Otherwise, instability  turbulent flow  critical Reynolds number
d
Laminar Turbulent
d
Forced convection: Non-dimensional groupings
Forced convection

30. les
x q
Ts
T
h=f(Fluid, Vel ,Distance,Temp)
•Fluid particle adjacent to the
solid surface is at rest
•These particles act to retard the
motion of adjoining layers
• boundary layer effect
Momentum balance: inertia forces, pressure gradient, viscous forces,
body forces
Energy balance: convective flux, diffusive flux, heat generation, energy
storage
FORCED CONVECTION:
external flow (over flat plate)
An internal flow is surrounded by solid boundaries that can restrict the
development of its boundary layer, for example, a pipe flow. An external flow, on
the other hand, are flows over bodies immersed in an unbounded fluid so that the
flow boundary layer can grow freely in one direction. Examples include the flows
over airfoils, ship hulls, turbine blades, etc.