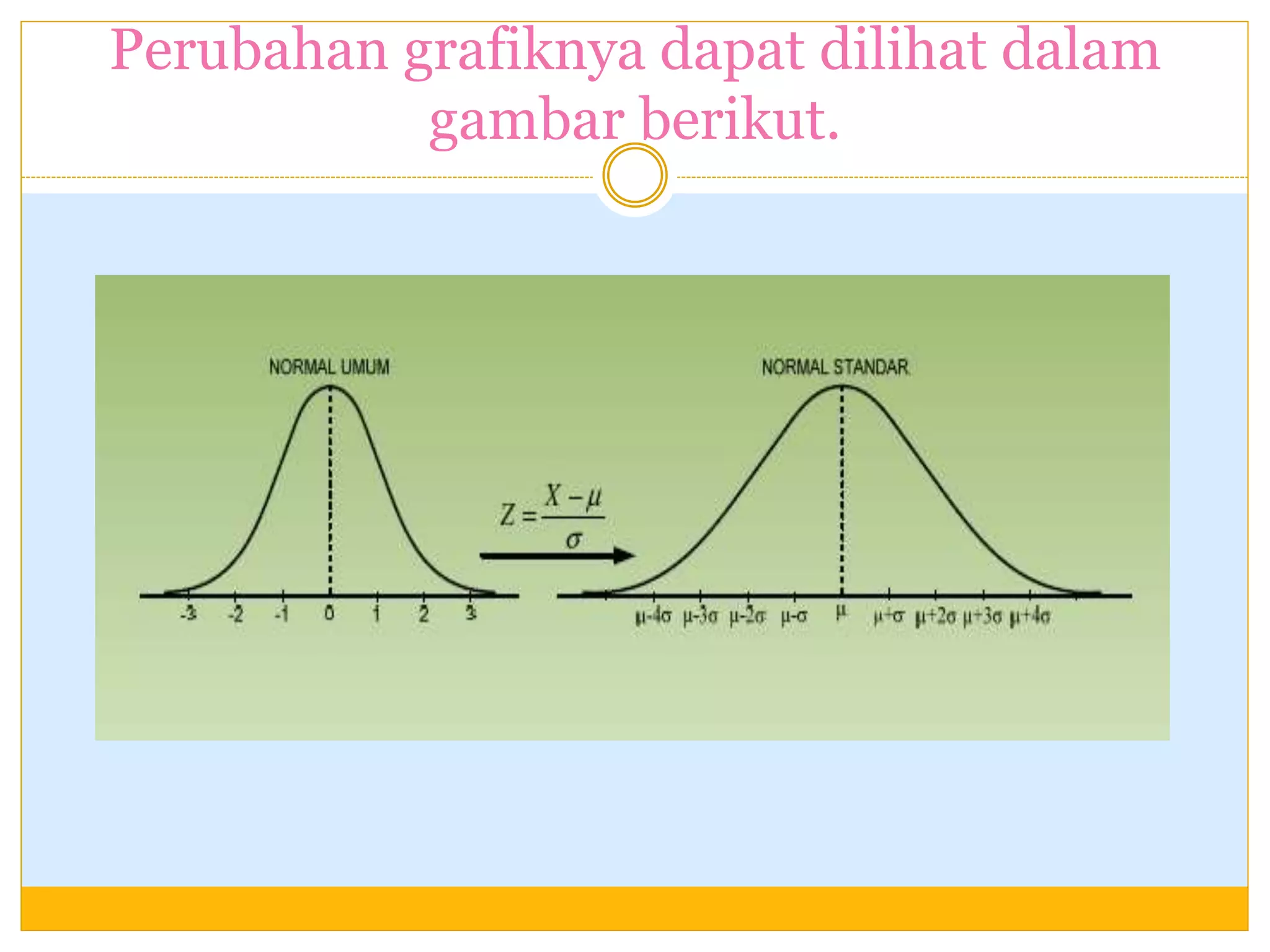
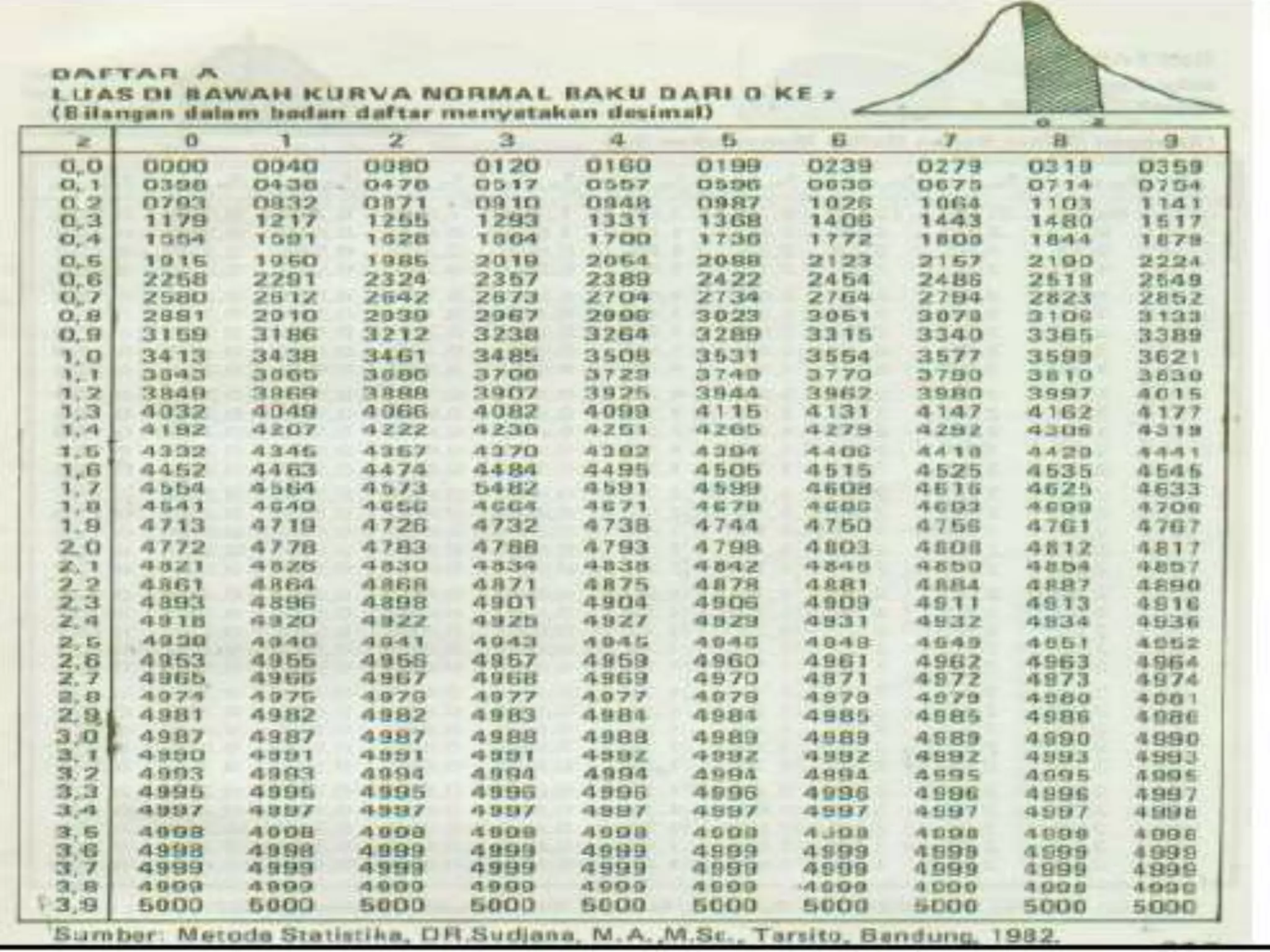
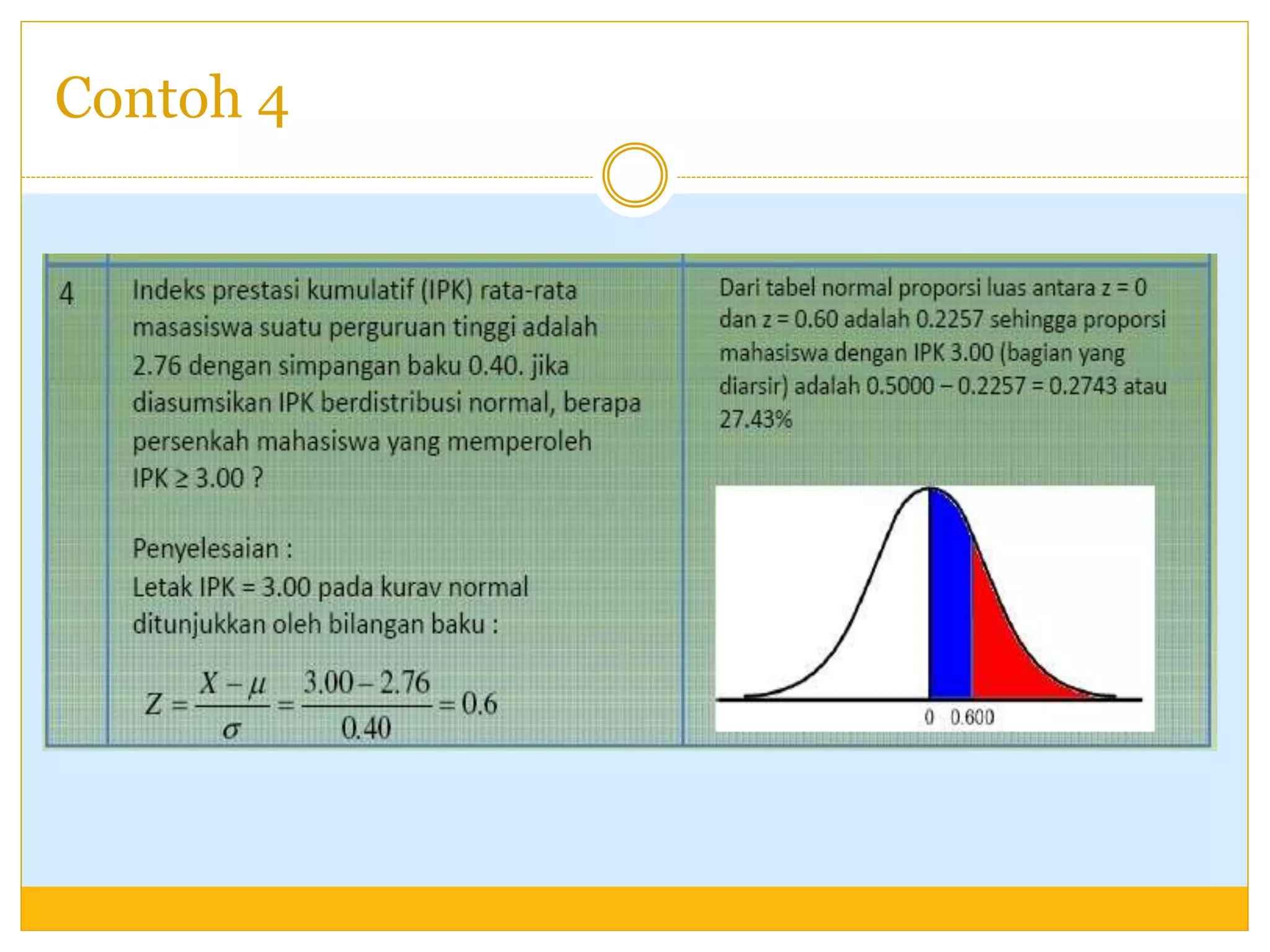
Dokumen ini memberikan penjelasan tentang distribusi normal, termasuk definisi, sifat-sifat, dan cara menghitung luas daerah di bawah kurva distribusi normal dengan contoh-contoh soal. Distribusi normal adalah salah satu distribusi yang paling penting dalam statistika yang memiliki bentuk lonceng dengan rata-rata sebagai sumbu simetris.

1. OLEH:
ANITA JULIANI ( 06081181419006)
PUTRI YANI ( 06081181419072)
SITI SHOLEKAH ( 06081181419011)
Distribusi Normal

2. Definisi
Distribusi normal sering disebut distribusi Gauss. Distribusi
normal menggunakan variabel acak kontinue dan merupakan
salah satu yang peling penting dan paling banyak digunakan.
Distribusi ini menyerupai bentuk lonceng (bell shape) dengan
nilai rata-rata x̄ sebagai sumbu simetrisnya.

3. Variabel kontinue X mempunyai fungsi densitas pada
X=x dinyatakan dengan persamaan:
Dengan:

4. Sifat-sifat penting distribusi normal:
 Grafiknya selalu ada diatas sumbu x (horizontal)
 Bentuknya simetrik terhadap sumbu y pada x = µ
 Mempunyai modus pada X = µ sebesar 0,3989/ σ
 Grafiknya mendekati sumbu datar x, dimulai dari x =
µ + 3σ ke kanan dan x = µ- 3σ ke kiri
 Luas daerah grafik = satu unit persegi
 Semakin besar σ, kurva semakin rendah (platikurtik)
 Semakin kecil σ, kurva semakin tinggi (leptokurtik)
 Kurva normal digunakan sebagai acuan pengujian
hipotesis jika ukuran sampel n ≥ 30

5. a. Leptokurtik b. platikurtik

6. Untuk mengubah distribusi normal umum
menjadi distribusi normal baku digunakan
rumus sebagai berikut.

7. Perubahan grafiknya dapat dilihat dalam
gambar berikut.

8. Cara mencari luas distribusi normal baku
 Hitung z sehingga dua desimal.
 Gambarkan kurvanya seperti gambar normal standar.
 Letakkan harga z pada sumbu datar, lalu tarik garis vertikal
hingga memotong kurva.
 Luas yang tertera dalam daftar adalah luas daerah antara
garis ini dengan garis tegak di titik nol.
 Dalam tabel normal cari tempat harga z pada kolom paling
kiri hanya satu desimal dan desimal keduanya dicari pada
baris paling atas.
 Dari z di kolom kiri maju ke kanan dan dari z di baris atas
turun ke bawah, maka didapat bilangan yang merupakan
luas yang dicari. Bilangan yang didapat harus dituliskan
dalam bentuk 0,xxxx (bentuk 4 desimal).

10. Contoh 1 Antara z= 0 dan z = 2,15
Cara pengerjaan:
Gunakan daftar f, dalam lampiran. Di bawah z pada
kolom kiri cari 2,1 dan di atas sekali 0,05. dari 2,1 maju
ke kanan dan dari 5 menurun, didapat 0,4842. luas
daerah yang dicari (diarsir) = 0,3842

11. Contoh 2 Antara z = 0 dan z = -1,86
Karena z bertanda negatif, maka pada grafiknya diletakkan di
sebelah kiri nol.
Untuk daftar digunakan z = 1,86. di bawah z kolom kiri
dapatkan 1.8 dan di atas angka 0,06.
Dari 1,8 ke kanan dan dari 6 ke bawah di dapat 0,4686.
Luas daerah= daerah diarsir= 0,4686

12. Contoh 3 Antara z = -1,50 dan z = 1,82
Dari grafik terlihat bahwa kita perlu mencari luas dua kali,
lalu dijumlahkan.
Mengikuti cara di (1) untuk z = 1,82 dan cara di (2) untuk z= -
1,50, maing-masing didapat 0,4656 dan 0, 4332.
Jumlahnya = luas= 0,4332 + 0,4656 = 0,8988

13. Contoh 4

14. TERIMA KASIH