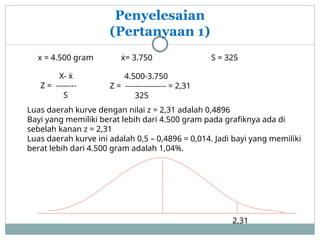
Kurva normal adalah distribusi simetris yang penting dalam statistik untuk menaksir dan meramalkan peristiwa. Karakteristiknya meliputi bentuk lonceng, kesetaraan mean, median, dan mode, serta luas total daerah di bawah kurva adalah satu. Kurva normal digunakan dalam statistik inferensial dan dapat dikombinasikan dengan standar deviasi untuk analisis distribusi data.

1. KURVA
NORMAL

2. Distribusi normal adalah distribusi yang memiliki
kurva yang berkesinambungan berbentuk simetris
DISTRIBUSI NORMAL
(Distribusi Gausse)
KURVE NORMAL
Suatu alat statistik yang
sangat penting untuk
menaksir dan meramalkan
peristiwa2 yang lebih luas
Suatu data membentuk
distribusi normal bila
jumlah data diatas dan
dibawah mean adalah
sama

3. KARAKTERISTIK
DISTRIBUSI KURVA NORMAL

1. Kurva berbentuk genta (= Md= Mo)
2. Kurva berbentuk simetris
3. Kurva normal berbentuk asimptotis. Kedua ekor
kurva memanjang tak berbatas dan pernah
memotong sumbu horizontal
4. Kurva mencapai puncak pada saat X= 
5. Luas daerah di bawah kurva adalah 1; ½ di sisi
kanan nilai tengah dan ½ di sisi kiri. Total=1

4. JENIS-JENIS
DISTRIBUSI NORMAL
0
1
2
3
4
5
6
7
8
9
10
m
Mesokurtic Platykurtic
Distribusi kurva normal dengan  sama dan 
berbeda

5. Distribusi kurva normal dengan  berbeda dan 
sama
Mangga “C”
Mangga “B”
Mangga “A”
150 300 450
JENIS-JENIS
DISTRIBUSI NORMAL

6. Distribusi kurva normal dengan  dan  berbeda
85 850
JENIS-JENIS
DISTRIBUSI NORMAL

7. KURVA NORMAL
Kurva Normal merupakan model teoritis sejenis
frekwensi poligon yang benar-benar simetris dan
mulus.
 Teori yang mendasari Statistik Inferensial
 Kurva Normal dikombinasikan dengan Standar Deviasi
dapat digunakan untuk membangun pernyataan deskriptif
yang tepat tentang distribusi empiris.

8. 1. Berbentuk lonceng berarti simetris di kanan dan kiri dari 'mean‘
2. 'Mean' = 'median' = 'mode', nilai dari ketiga ukuran sentral ini terletak pada titik
yang sama pada sumbu X dan hanya mempunyai satu 'mode' (unimodal).
3. Jumlah seluruh daerah diatas sumbu X dan dibawah kurva setara dengan satu
atau seratus persen. Karena kurva Normal simetris,berbentuk lonceng dan
unimodal maka daerah di di kanan dan di kiri garis tegak lurus diatas
meanmasing-masing besarnya 0,5 atau 50%.
4. Kurva ditetapkan oleh dua parameteryaitu 'mean' yang merupakan pusat atau
konsentrasi distribusi dan standar deviasi yang menentukan penyebaran
distribusi di sekitar 'mean'.
5. Ujung-ujung kurva meruncing dikanan dan kiri tetapi tidak pernah mennyentuh
garis X (asymptotic), dan jarak keujungujungnya dari 'mean' menujukkan
tingkat frekuensi pengukuran.
6. Bila garis tegak lurus dibuat pada jarak satu standar deviasi di kanan dan di kiri
'mean' akan mencakup daerah seluas kira-kira 68% di dalamnya (antara garis
tersebut, kurva dan sumbu bila dua standard deviasi 95%, bila tiga standar
deviasi 99,7% dan area di luar tiga
Konsep Dasar Kurva Normal

9. Daerah Kurva Normal
Ruangan yang dibatasi daerah kurve dengan absisnya disebut
daerah kurve normal. Luas daerah kurve normal biasa dinyatakan
dalam persen atau proporsi. Dengan kata lain luas daerah kurve
normal adalah 100% (apabila dinyatakan dalam prosen) dan apabila
dinyatakan dalam dengan proporsi maka luas daerah kurve normal
adalah 1 (satu).

10. Kurva normal standard
(kurva normal baku)
 Nilai Z Nilai Standar Konversi Nilai asli ke Standar Deviasi
 Nilai Z  untuk menemukan prosentase wilayah total di
bawah kurva normal

11. Contoh soal
Contoh:
Berat bayi yang baru lahir rata-ratanya 3.750
gram dengan simpangan baku 325 gram. Jika
berat bayi berdistribusi normal, maka
tentukanlah/hitunglah:
1.Berapa prosen bayi yang beratnya lebih dari
4.500 gram?
2.Berapa bayi yang beratnya 3.500 gram dan
4.500 gram, jika semuanya ada 10.000 bayi?

12. Cara menjawab soal
1. Hitung nilai z sampai dengan dua desimal.
2. Gambar kurve normal standar.
3. Letakkan harga z pada sumbu datar lalu tarik garis
vertikal hingga memotong kurve.
4. Lihat harga z dalam daftar harga z, caranya cari
haarga z pada kolom paling kiri sampai satu desimal
dan desimal keduanya dicari pada baris paling atas.
5. Dari z paling kiri maju ke ka kanan dari dari z di baris
atas turun ke bawah, maka didapat bilangan dalam
bentuk 0,…… (bentuk empat desimal)
6. Apabila yang diperlukan prosen maka setelah melalui
langkah ke lima kalikan dengan 100.

13. Penyelesaian
(Pertanyaan 1)
x = 4.500 gram ẋ= 3.750 S = 325
X- ẋ
Z = --------
S
4.500-3.750
Z = ---------------- = 2,31
325
Luas daerah kurve dengan nilai z = 2,31 adalah 0,4896
Bayi yang memiliki berat lebih dari 4.500 gram pada grafiknya ada di
sebelah kanan z = 2,31
Luas daerah kurve ini adalah 0,5 – 0,4896 = 0,014. Jadi bayi yang memiliki
berat lebih dari 4.500 gram adalah 1,04%.
2,31

14. PENYELESAIAN
(PERTANYAAN 2)
x = 4.500 gram ẋ= 3.750 S = 325
3.500-3.750
Z = ---------------- = 0,77
325
Luas daerah kurve dengan nilai z = 0,77 adalah 0, 2794 DAN Luas daerah kurve
dengan nilai z = 2,31 adalah 0, 4896
Grafik bayi yang memiliki berat lebih dari 3.750 dan 4.500 gram ada di antara z =
0,77 dan z = 2,31
Luas daerahnya adalah 0,2794 + 0,4896 = 0,7690.
Jadi banyaknya bayi yang memiliki berat lebih dari dari 3.750 gram s/d 4.500 gram
adalah 7.690 (0,7690 x 10.000)
2,31
4.500-3.750
Z = ---------------- = 2,31
325
0,77

16. TUGAS KE 2
IPK mahasiswa rata-ratanya 3.25 dengan
simpangan baku 0,32. Jika IPK mahasiswa
berdistribusi normal, maka
tentukanlah/hitunglah:
1.Berapa prosen mahasiswa yang IPK nya lebih
dari 3.5?
2.Berapa jumlah mahasiswa yang IPK nya
antara 2.90 s/d 3.25, jika jumlah mahasiwa
semuanya ada 2.000 mahasiswa?