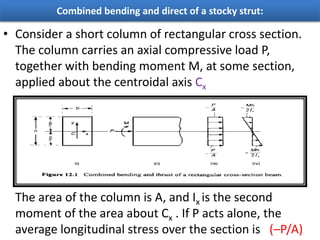
The document discusses the concepts of direct and bending stresses in materials under axial loads, explaining how these stresses can be combined to find the overall effect on a structure. It details the algebraic addition of stress types and introduces cases of eccentric loading, outlining conditions for avoiding tensile stress in structural members. The document also provides limits of eccentricity for different cross-sectional shapes to maintain structural integrity.