This document summarizes a seminar presentation on principal stresses and strains. It defines principal stresses as planes that experience only normal stresses and no shear stress. It then provides equations to calculate normal and shear stresses on oblique planes for members subjected to various loading conditions, including direct stress in one direction, direct stresses in two perpendicular directions, simple shear stress, and combinations of these. It derives equations to determine the position of principal planes and maximum shear stress. Examples are given for special cases where some stresses or shear terms are zero.

1. AHEMEDABAD INSTITUTE
OF TECHNOLOGY
SEMINAR
Principal stresses and strains

2. CIVIL ENGINEERING (3rd sem)B.E
SUBJECT: Mos
Submitted by:
 Patel Bhavik
 Patel Parth
 Patel Garvish
 Jigar
 Milan

3. Stresses and strains
 In last lecture we looked at stresses were acting
in a plane that was at right angles/parallel to the
action of force.

5. Principal stresses and
strains
 What are principal stresses.
 Planes that have no shear stress are
called as principal planes.
 Principal planes carry only normal
stresses

6. Stresses in oblique plane
 In real life stresses does not act in normal
direction but rather in inclined planes.

7. σ =
𝑃
𝐴
P = Axial forces
A = cross
sectional area
𝜎 𝑛 = 𝜎𝑐𝑜𝑠 2
θ
𝜎𝑡 =
𝜎
2
sin2θ

8.  Member subjected to direct
stress in one plane
 Member subjected to direct
stress in two mutually
perpendicular plane.
 Member subjected to simple
shear stress.
 Member subjected to direct
stress in two mutually
perpendicular directions +
simple shear stress.

9.  Member subjected to direct stress in two
mutually
perpendicular directions + simple shear stress
σn =
𝜎1+𝜎2
2
+
𝜎1−𝜎2
2
cos2θ+τsin2θ
𝜎𝑡 =
𝜎1−𝜎2
2
sin2θ−τcos2θ

10.  Member subjected to direct stress in two
mutually
perpendicular directions + simple shear stress
 POSITION OF PRINCIPAL PLANES
 Shear stress should be zero
𝜎𝑡 =
𝜎1−𝜎2
2
sin2θ−τcos2θ=0
tan2θ = 2T/(𝜎1 - 𝜎2 )

11.  Member subjected to direct stress in two mutually
perpendicular directions + simple shear stress .
Major principal Stress=
𝜎1+𝜎2
2
+
𝜎1−𝜎2
2
+ T
Minor principal Stress =
𝜎1+𝜎2
2
+
𝜎1−𝜎2
2
+ T

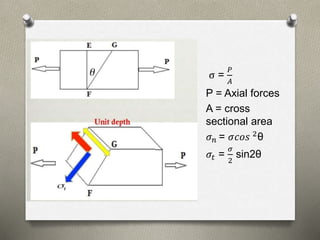
12.  Member subjected to direct stress in two
mutually perpendicular directions + simple
shear stress
 MAX SHEAR STRESS
𝑑
𝑑𝜃
(𝜎𝑡 ) = 0
𝑑
𝑑𝜃
[𝑡𝑎𝑛2𝜃sin2θ−τcos2θ ] = 0
tan2θ =
𝜎1−𝜎2
2𝑇

13.  Member subjected to direct stress in two
mutually perpendicular directions + simple
shear stress
 MAX SHEAR STRESS
𝜎𝑡 =
𝜎1−𝜎2
2
sin2θ−τcos2θ
tan2θ =
𝜎1−𝜎2
2𝑇
𝜎𝑡(max ) =
1
2
((𝜎1 − 𝜎2 )2 + 4𝑇2

14.  Member subjected to direct stress in one plane
 Member subjected to direct stress in two
mutually
perpendicular plane
 Member subjected to simple shear stress.
 Member subjected to direct stress in two
mutually
perpendicular directions + simple shear stress

15.  Member subjected to direct stress in one plane
𝜎 𝑛 =
𝜎1+𝜎2
2
+
𝜎1−𝜎2
2
cos2θ+τsin2θ
𝜎𝑡 =
𝜎1−𝜎2
2
sin2θ−τcos2θ
Stress in one direction and no shear stress σ2
=0,τ=0
𝜎 𝑛 =
𝜎1
2
+
𝜎1
2
cos2θ = σ1 cos2
𝜃
𝜎𝑡 =
𝜎1
2
sin2θ

16.  Member subjected to direct stress in two mutually
perpendicular plane
𝜎 𝑛 =
𝜎1+𝜎2
2
+
𝜎1−𝜎2
2
cos2θ+τsin2θ
𝜎𝑡 =
𝜎1−𝜎2
2
sin2θ−τcos2θ
Stress in two direction and no shear stress τ=0
𝜎 𝑛 =
𝜎1+𝜎2
2
+
𝜎1−𝜎2
2
cos2θ
𝜎𝑡 =
𝜎1−𝜎2
2
sin2θ

17.  Member subjected to simple shear stress.
𝜎 𝑛 =
𝜎1+𝜎2
2
+
𝜎1−𝜎2
2
cos2θ+τsin2θ
𝜎𝑡 =
𝜎1−𝜎2
2
sin2θ−τcos2θ
No stress in axial direction but only shear stress σ1=σ2
=0
𝜎 𝑛 = τsin2θ
𝜎𝑡 = −τcos2θ