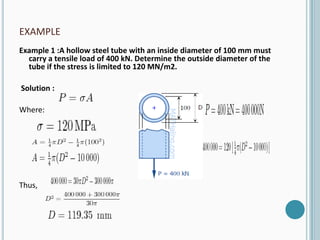
The document discusses stress in mechanics as a measure of internal forces in materials, focusing on types of stress such as axial, shear, and bearing stress. It elaborates on axial force definitions, the concept of a geometric center, and the nature of axial stress, distinguishing between compressive and tensile stress with practical examples. The document further outlines essential assumptions related to axial stress applications and provides an example problem involving tensile load calculations.

2. INTRODUCTION

5. SOMETHING LIKE THIS:

6. ON A SERIOUS NOTE STRESS IN MECHANICS IS

a physical quantity that expresses the
internal forces that neighboring particles of
a continuous material exert on each other.

For example, when a solid vertical bar is supporting
a weight, each particle in the bar pulls on the particles
immediately above and below it.

7. When some external system of forces or loads act on a
body ,the internal forces ( equal and opposite) are set up
at various sections of the body, which resists the external
forces .
 This internal force per unit area at any section of the
body is known as unit stress or simply stress.


Where, F = FORCE or LOAD acting on the body, and
A = Cross-sectional area of the body.
0

8.  The
force applied tends to deflect the body .Due to
cohesion between the molecules, the body resists
deformation.
 Simple
Stresses are mainly of 4 types:
1.Axial or Normal Stress
2. Shear Stress
3.Bearing Stress
4.Thin-walled Pressure Vessel
 So, some sort of force is required in a direction to
calculate the stress

9. LET US NOW SEE WHAT DOES AXIAL FORCE REFERS TO:
An axial force is any force that directly acts through or
parallel to the major axis of an object.
 These forces are typically stretching force or
compression force, depending on direction.
 In addition, when the force load is even across the
form’s geometric center, it is concentric, and when it is
uneven, it is eccentric. Unlike many acting forces, an
axial force is often its own counter; an object pulled or
pushed evenly in opposing directions doesn’t move.
Sheer force occupies a similar position to axial force, but
operates perpendicular to the center axis of the object.


10.  One
of the most important parts of examining
axial forces is the idea of a geometric center.
 This is a point within the boundaries of a solid
object that is the perfect center of the entire
mass.
 In a simple object, such as a cylinder, it is easy
to find the exact middle of the object by simply
measuring the sides. In a complex object, such
as a bicycle, the process is much more
complicated.

11. AXIAL MEMBERS
which support load only along their primary axis, are the
most basic of structural members. Equilibrium requires
that forces in Axial Members are always Equal, Opposite,
and Co-Linear. In most cases, axial members have
pinned ends.
 Some examples of axial members include:
1.Bars;
2.Truss Members;
3.Ropes and Cables. etc


12. THEREFORE AXIAL STRESS IS,
defined as the force perpendicular to the cross sectional
area of the member divided by the cross sectional area.
If a cut is taken perpendicular to a bar's axis, exposing an
internal cross-section of area A, the force per unit area
on the face of this cut is termed AXIAL STRESS.
 The symbol used for axial stress in most engineering
texts is (sigma).
 Stress is positive in tension (P>0) and negative in
compression (P<0);
English units: psi (pounds per square inch), or ksi
(kilopounds per square inch);


13. Stress caused in axial direction due to axial force.
 Generally two types of axial stress are there :

1.compressive axial stress
2.tensile axial stress

14. 
Compressive stress is axial stress that tends to cause a
body to become shorter along the direction of
applied force.

Tensile stress is axial stress that tends to cause a body
to become longer along the direction of applied
force.

15. EXAMPLES OF TENSILE AXIAL STRESS INCLUDE

a chain carrying a load and tension cables on a bridge.

16. EXAMPLES OF COMPRESSIVE AXIAL STRESS INCLUDE

decorative columns in architecture and the steel
structure of a high rise building.

17. SOME ASSUMPTIONS REGARDING AXIAL STRESS
Loads pass through the centroid of the section
 Member should be straight
 Load less than buckling load
 stress,
 Stress is positive in tension (P>0) and negative in
compression (P<0).


18. EXAMPLE
Example 1 :A hollow steel tube with an inside diameter of 100 mm must
carry a tensile load of 400 kN. Determine the outside diameter of the
tube if the stress is limited to 120 MN/m2.
Solution :
Where:
Thus,

20. Question