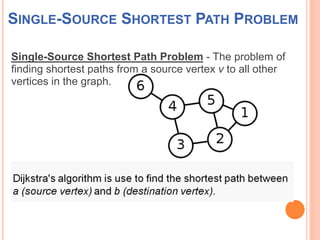
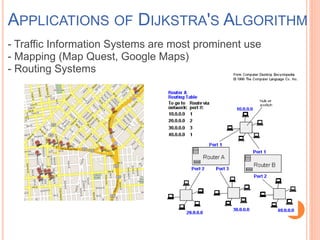
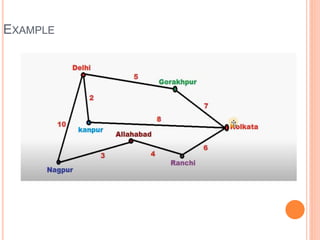
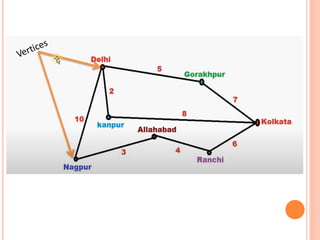
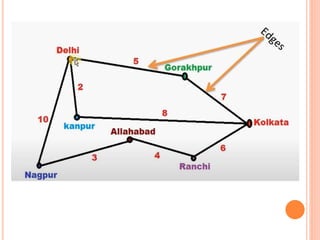
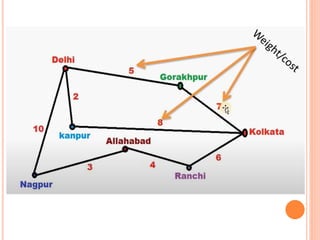
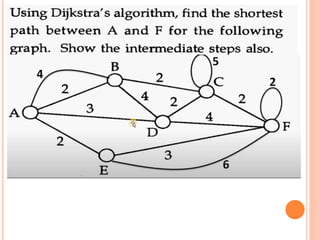
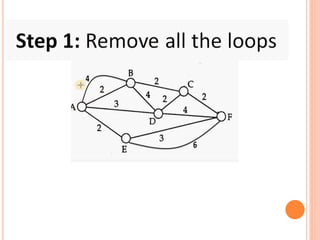
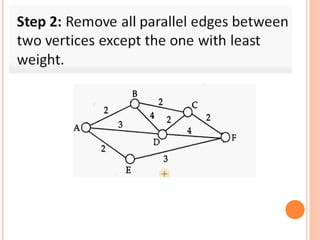
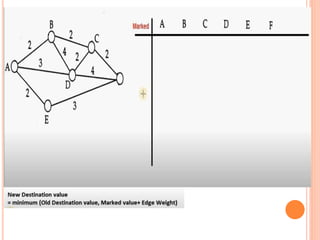
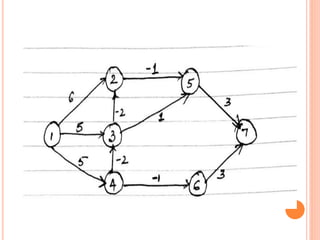
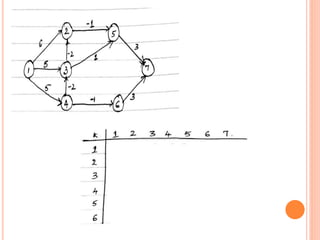
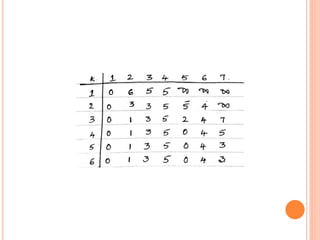
This document discusses Dijkstra's algorithm, which is a solution to the single-source shortest path problem in graph theory. It finds the shortest paths from a source vertex to all other vertices in a graph. Dijkstra's algorithm works for both directed and undirected graphs as long as all edge weights are non-negative. It uses a greedy approach to iteratively mark the vertex with the smallest distance from the source and update the distances of neighboring vertices. The document also notes that while Dijkstra's algorithm is computationally expensive, it can be used anytime the shortest path to another vertex is needed once the origin is determined. Applications include traffic information systems, mapping, and routing systems.

1. DIJKSTRA'S ALGORITHM

2. THE AUTHOR: EDSGER WYBE DIJKSTRA
"Computer Science is no more about computers than
astronomy is about telescopes."
http://www.cs.utexas.edu/~EWD/

3. SINGLE-SOURCE SHORTEST PATH PROBLEM
Single-Source Shortest Path Problem - The problem of
finding shortest paths from a source vertex v to all other
vertices in the graph.

4. DIJKSTRA'S ALGORITHM
Dijkstra's algorithm - is a solution to the single-source
shortest path problem in graph theory.
Works on both directed and undirected graphs. However, all
edges must have nonnegative weights.
Approach: Greedy
Input: Weighted graph G={E,V} and source vertex v∈V, such
that all edge weights are nonnegative
Output: Lengths of shortest paths (or the shortest paths
themselves) from a given source vertex v∈V to all other
vertices

5. DIJKSTRA'S ALGORITHM - WHY IT WORKS
 As with all greedy algorithms, we need to make sure that it
is a correct algorithm (e.g., it always returns the right solution
if it is given correct input).

6.  As mentioned, Dijkstra’s algorithm calculates the
shortest path to every vertex.
 However, it is about as computationally expensive
to calculate the shortest path from vertex u to
every vertex using Dijkstra’s as it is to calculate the
shortest path to some particular vertex v.
 Therefore, anytime we want to know the optimal
path to some other vertex from a determined
origin, we can use Dijkstra’s algorithm.
DIJKSTRA'S ALGORITHM - WHY USE IT?

7. APPLICATIONS OF DIJKSTRA'S ALGORITHM
- Traffic Information Systems are most prominent use
- Mapping (Map Quest, Google Maps)
- Routing Systems

8. EXAMPLE

15. Step:3
i. Set 0 to the source vertex and infinite to the remaining vertices.
For all vertices, repeat (ii) and (iii)
ii. Mark the smallest unmarked value and mark that vertex.
iii. Find those vertices which are directly connected with marked vertex
and update all ( known as Relaxation)
New Destination value : min(Old Destination value, Marked value +
Edge Weight)

20. BELLMAN FORD ALGORITHM
(Distance Vector)
If the weighted graph contains the negative weight values, then the
Dijkstra algorithm does not confirm whether it produces the correct
answer or not. In contrast to Dijkstra algorithm, bellman ford
algorithm guarantees the correct answer even if the weighted graph
contains the negative weight values.