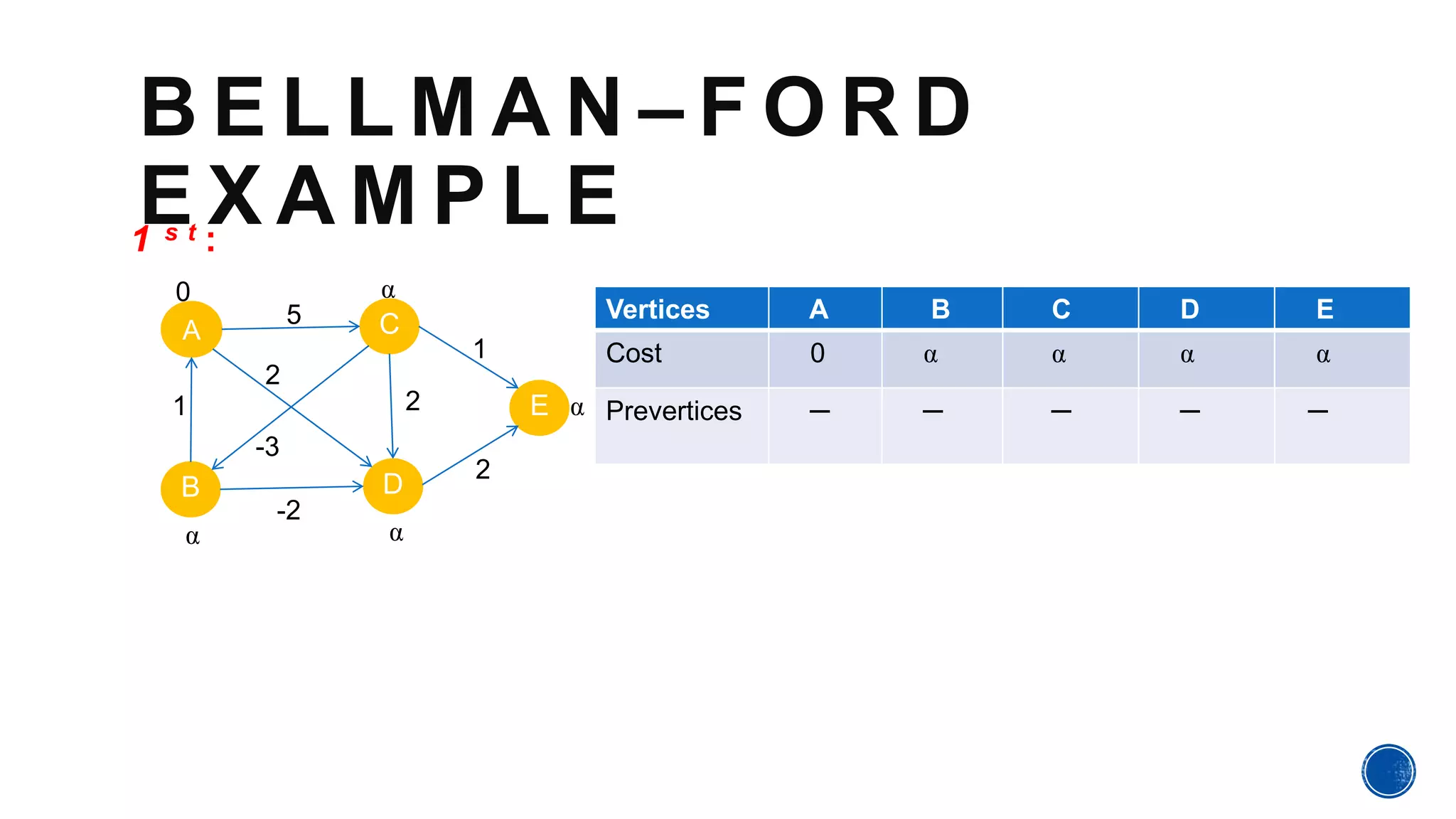
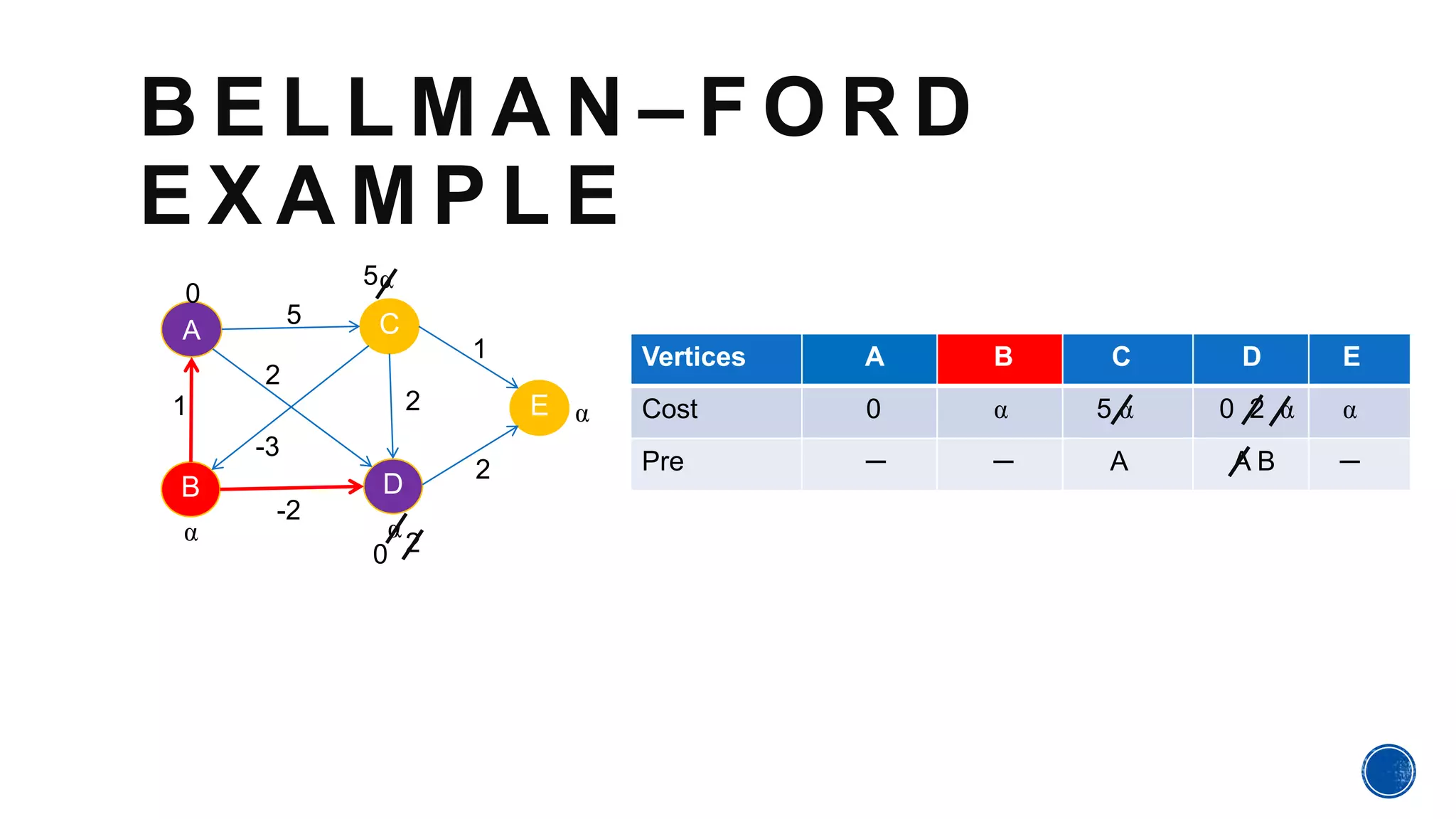
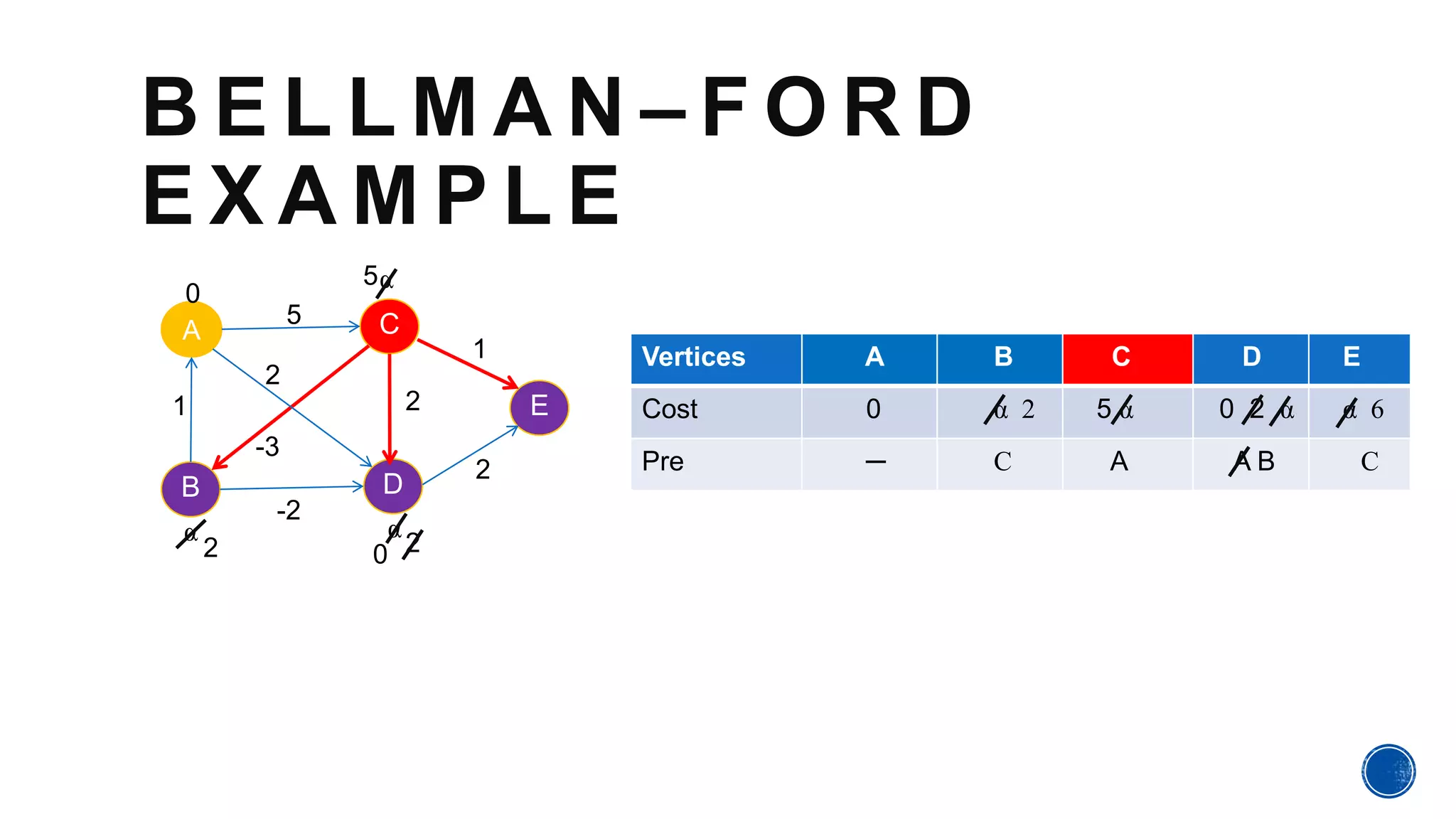
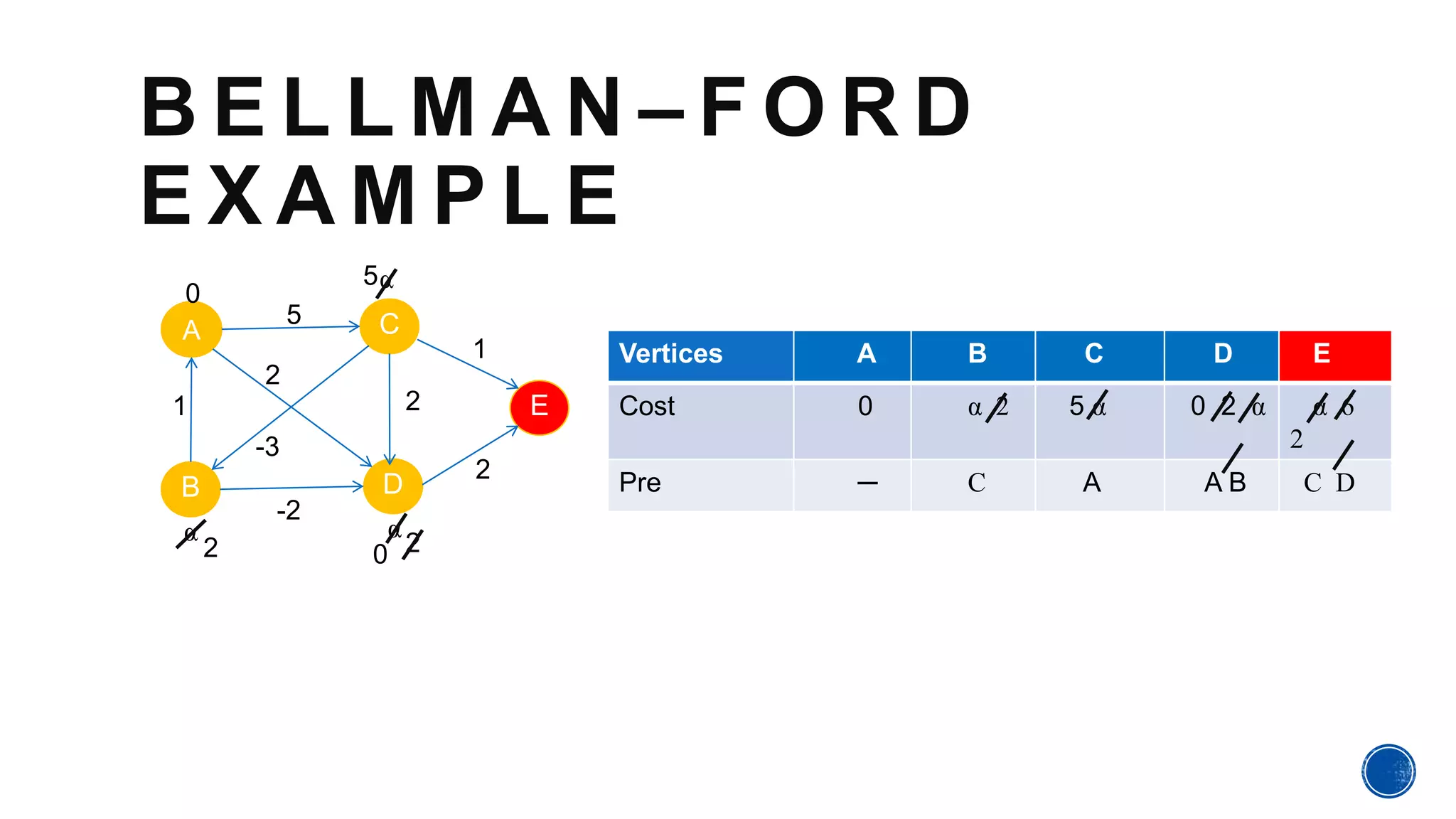
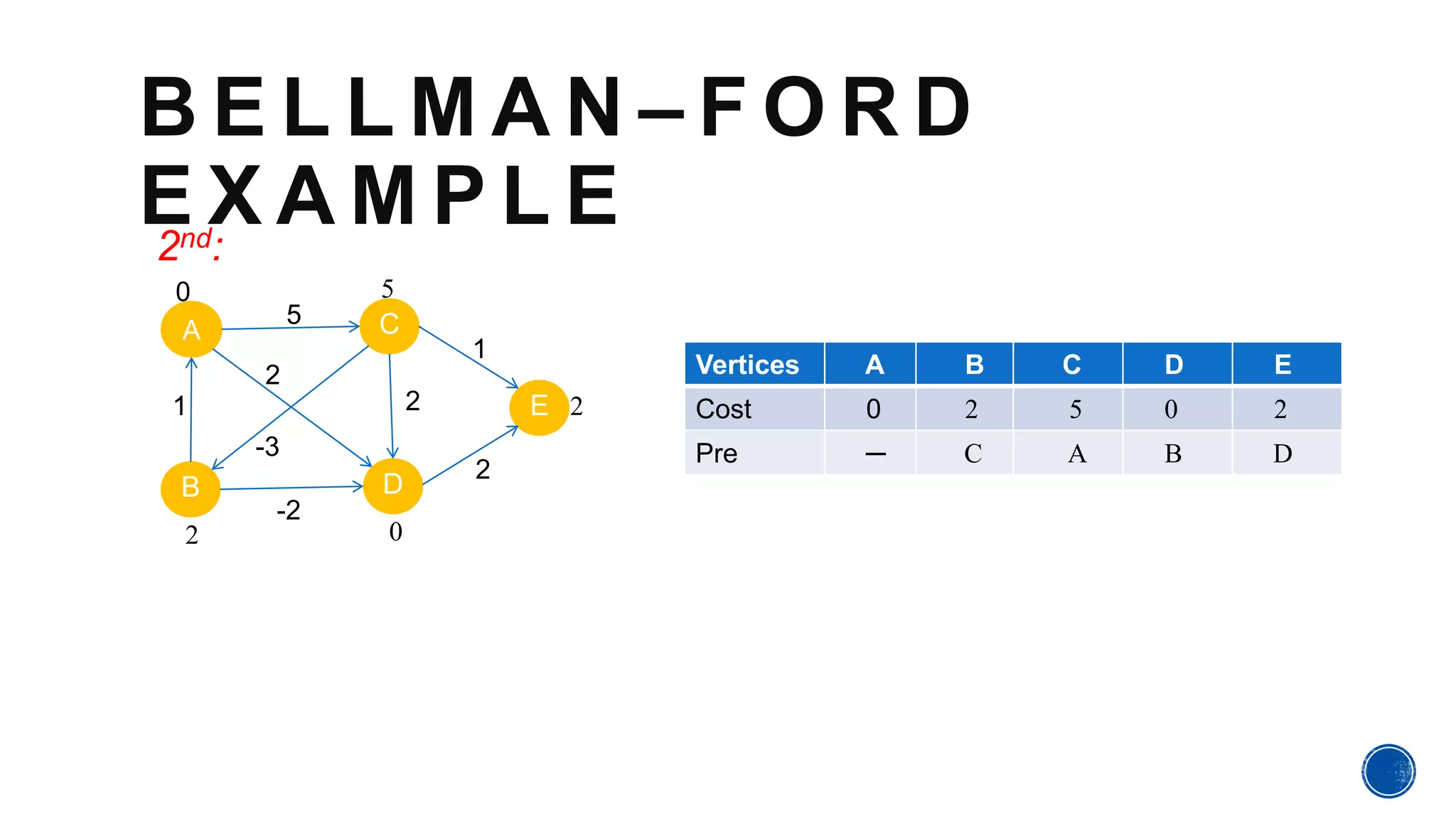
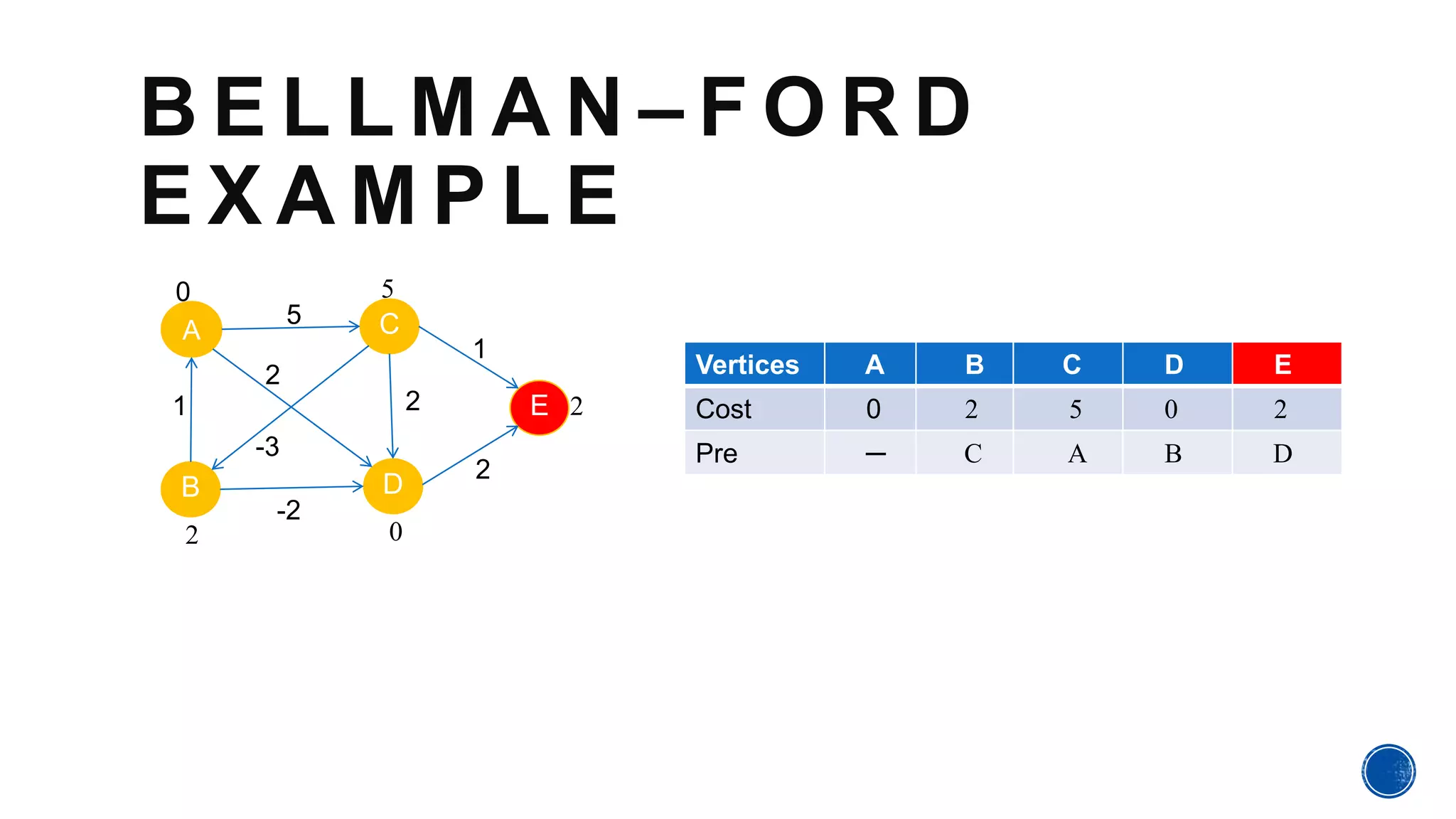
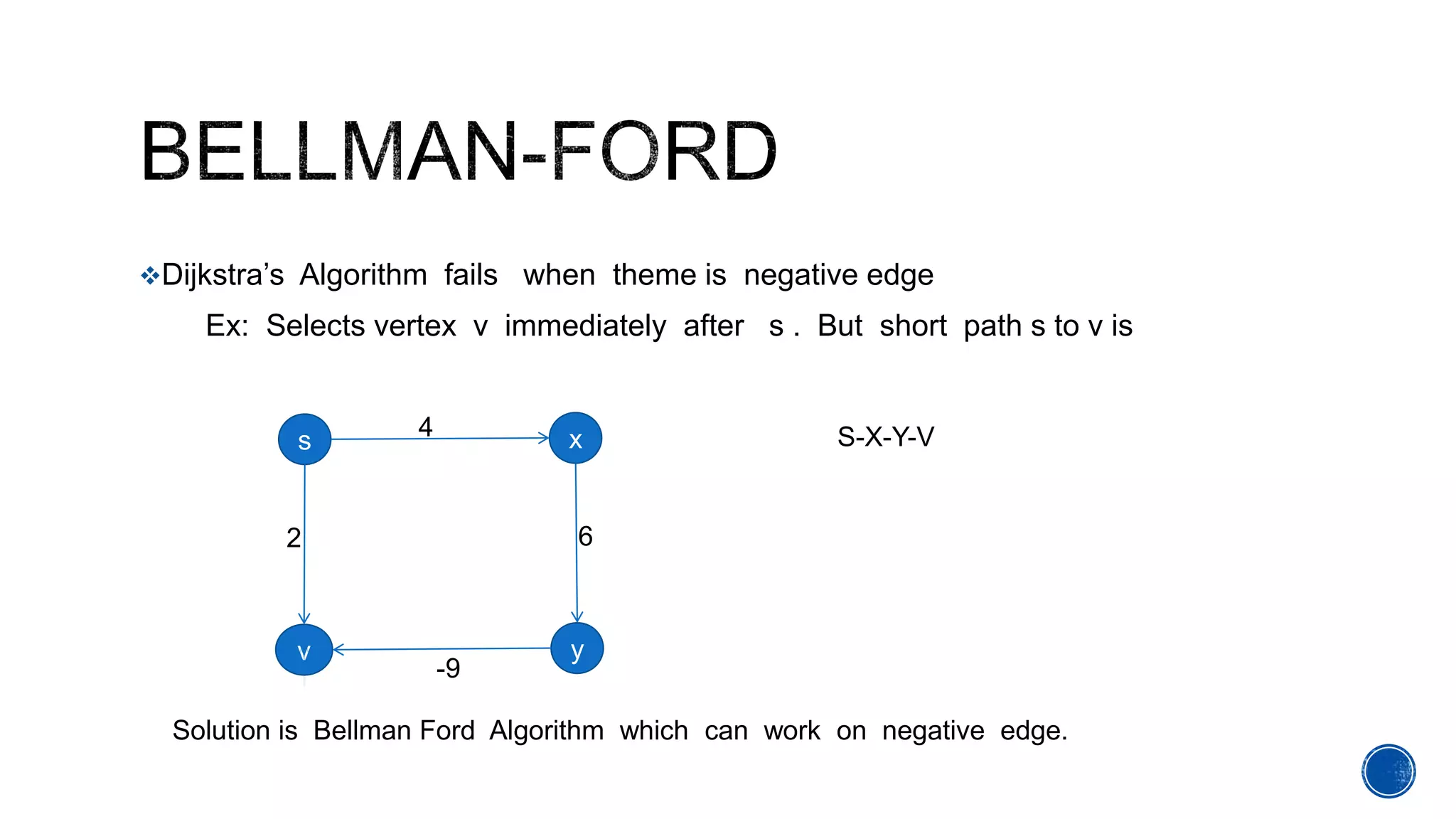
The Bellman-Ford algorithm, proposed by Richard Bellman and Lester Ford Jr., is designed to find the shortest paths in graphs that may contain negative edge weights. It can detect negative cycles, which can affect the existence of a shortest path, making it a valuable tool in various applications. The algorithm processes each edge iteratively to ensure accurate path cost calculations from a source to all other vertices.

1. BELLMAN
FORD
ALGORITHM
MD.SAJJADUL ISLAM
ID: 172-35-2088
SOFTWARE ENGNIEERING
DAFFODIL INTERNATIONAL UNIVERSITY

2. B E L L M A N - F O R D
Richard E. Bellman Lester R.Ford ,Jr.

3. • The algorithm was first proposed by Alfonso Shimbel
in 1955
• Named after Richard Bellman and Lester Ford Jr who
published it in 1956 and 1958
• Edward F. Moore also published the same algorithm
in 1957, and for this reason it is also sometimes
called the Bellman–Ford–Moore algorithm

4. B E L L M A N – F O R D
A L G O R I T H M
 Negative edge weights are found in various applications of graphs,
hence the usefulness of this algorithm. If a graph contains a "negative
cycle" ( a cycle whose edges sum to a negative value) that is reachable
from the source, then there is no cheapest path: any path that has a
point on the negative cycle can be made cheaper by one more walk
around the negative cycle. In such a case, the Bellman–Ford algorithm
can detect negative cycles and report their existence.

5. S H O R T E S T PAT H
P R O B L E M
Shortest path network
Driected graph
Source s, Destination t
Cost(V-U) cost of using edge from v to u
Shortest path problem
Find shortest directed path from s to t
Cost of path = sum of arc cost in path
δ (S , Vi-1) + W(Vi-1,Vi)
Vi
V1
V2
V3
δ (S , Vi)=

6. Dijkstra’s Algorithm fails when theme is negative edge
Ex: Selects vertex v immediately after s . But short path s to v is
s x
v y
4
6
-9
2
S-X-Y-V
Solution is Bellman Ford Algorithm which can work on negative edge.

7. BELLMAN-FOR D ( G ,s )
INITIALIZE SINGLE – SOURCE ( G , s )
for i 1 to |V|-1 do computaion
for each edge ( u, v ) € G.E do
RELAX ( U , V )
for each edge ( u, v ) € E do
if d[V] > d[U] + W( U , V ) then check
return FALSE
return TRUE

8. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
Vertices A B C D E
Cost 0 α α α α
Prevertices ─ ─ ─ ─ ─1
5
2
-3
-2
2
1
2
0 α
α α
α
1 s t :

9. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
1
5
2
-3
-2
2
1
2
0
5α
α α
α
2
Vertices A B C D E
Cost 0 α 5 α 2 α α
Pre ─ ─ A A ─

10. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
1
5
2
-3
-2
2
1
2
0
5α
α α
α
20
Vertices A B C D E
Cost 0 α 5 α 0 2 α α
Pre ─ ─ A A B ─

11. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
1
5
2
-3
-2
2
1
2
0
5α
α α
202
Vertices A B C D E
Cost 0 α 2 5 α 0 2 α α 6
Pre ─ C A A B C

12. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
1
5
2
-3
-2
2
1
2
0
5α
α α
202
Vertices A B C D E
Cost 0 α 2 5 α 0 2 α α 6 2
Pre ─ C A A B C D

13. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
1
5
2
-3
-2
2
1
2
0
5α
α α
202
Vertices A B C D E
Cost 0 α 2 5 α 0 2 α α 6
2
Pre ─ C A A B C D

14. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
Vertices A B C D E
Cost 0 2 5 0 2
Pre ─ C A B D
1
5
2
-3
-2
2
1
2
0 5
2 0
2
2nd:

15. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
Vertices A B C D E
Cost 0 2 5 0 2
Pre ─ C A B D
1
5
2
-3
-2
2
1
2
0
2 0
2
5

16. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
Vertices A B C D E
Cost 0 2 5 0 2
Pre ─ C A B D
1
5
2
-3
-2
2
1
2
0
2 0
2

17. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
Vertices A B C D E
Cost 0 2 5 0 2
Pre ─ C A B D
1
5
2
-3
-2
2
1
2
0
2 0
2

18. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
Vertices A B C D E
Cost 0 2 5 0 2
Pre ─ C A B D
1
5
2
-3
-2
2
1
2
0
2 0
2

19. B E L L M A N – F O R D
E X A M P L E
A
B D
E
C
Vertices A B C D E
Cost 0 2 5 0 2
Pre ─ C A B D
1
5
2
-3
-2
2
1
2
0 5
2 0
2

20. B E L L M A N – F O R D
E X A M P L E
Vertices A B C D E
Cost 0 2 5 0 2
Pre ─ C A B D
A
B D
E
C
1
5
2
-3
-2
2
1
2
0 5
2 0
2
Shortest path are –
E = ACBDE = {5+(-3)+(-2)+2 }= 2