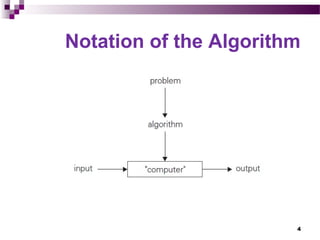
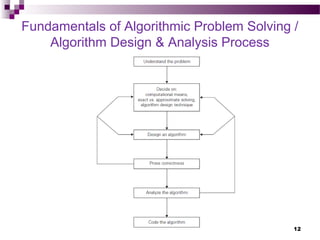
The document introduces algorithms, outlining their definition, design, and implementation steps while highlighting important problem types and fundamental data structures. It explains the concept of algorithms through examples like finding the greatest common divisor (gcd) and generating prime numbers. The document also touches on algorithm efficiency, correctness, and various problem-solving techniques.

1. The Design and
Analysis of
Algorithms
by Anany Levitin

2. 2
CHAPTER 1: INTRODUCTIONCHAPTER 1: INTRODUCTION
 What is an Algorithm
 Steps in Designing and Implementing
an Algorithm
 Important Problem Types
 Fundamental Data Structures

3. 3
ALGORITHM
 A sequence of unambiguous
instructions for solving a problem,
i.e. for obtaining the required
output for any legitimate input in
a finite amount of time

4. Notation of the Algorithm
4

5. 5
Special Features of Algorithms
 Non-ambiguity
 Range of inputs
 The same algorithm can be represented
in different ways
 Several algorithms for solving the
same problem
 Different algorithms with different
speeds

6. Find the GCD(m,n)
Method 1: Descriptive Algorithm
6

7. GCD using Euclid’s Method
gcd(m,n)=gcd(n,m nod n)
Find:
1. GCD(124,12)
2. GCD(160,15)
3. GCD(338,22)
4. GCD(150,8)
7

8. Find the GCD(m,n)
Method 2:
Descriptive Algorithm
8

9. Find the GCD(m,n)
Method 2: Pseudocode Representation
9

10. Find the set of all Prime
numbers
Method 1: Middle School Level
Find Set of ALL Prime Numbers within 25
10

11. Find the set of all Prime
numbers
Method 2: Sieve of Erathosthenes
Find Set of ALL Prime Numbers within 25
11

12. Fundamentals of Algorithmic Problem Solving /
Algorithm Design & Analysis Process
12

13. 13
What does it mean to understand
the problem?
 What are the problem objects?
 What are the operations applied to the objects?
Deciding on computational
means
 How the objects would be represented?
 How the operations would be implemented?

14. 14
Design an algorithm
• Build a computational model of the
solving process
Prove correctness
• Correct output for every legitimate input
in finite time
• Based on correct math formula
• By induction

15. 15
Analyze the algorithm
Efficiency: time and space
Simplicity:
Generality: range of inputs, special cases
Optimality: no other algorithm can do better
Coding
How the objects and operations in the
algorithm are represented in the chosen
programming language?

16. 16
Important problem types
 Sorting
 Searching
 String processing
 Graph problems
 Combinatorial problems
 Geometric problems
 Numerical problems

17. 17
Fundamental data structures
Linear data structures
 Array
 Linked list
 Stack
 Queue
Operations: search, delete, insert
Implementation: static, dynamic

18. 18
Non-linear data structures
 Graphs
 Trees : connected graph without cycles
Rooted trees
 Ordered trees
Binary trees
Graph representation: adjacency lists,
adjacency matrix
Tree representation: as graphs; binary nodes
Fundamental data structures

19. 19
Fundamental data structures
Sets, Bags, Dictionaries
 Set: unordered collection of distinct elements
Operations: membership, union, intersection
Representation: bit string; linear structure
 Bag: unordered collection,
elements may be repeated
 Dictionary: a bag with operations search, add,
delete

20. 20
Conclusion
 Algorithm classification
By types of problems
By design technique
 Design techniques
a general approach to solving problems

21. Check if you are Clear with:
 Definition of Algorithm
 Notation of Algorithm
 Examples: GCD and Prime
 Fundamentals of Algorithms / Process of
Design & Analysis of Algorithms
 Types of Problems
 Fundamental Data Structures
21

22. Have a GREAT Day..!!!
22