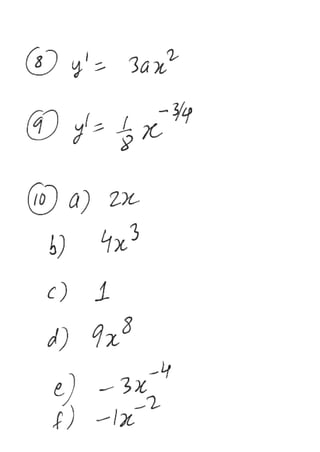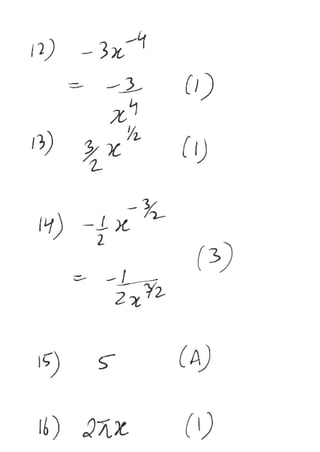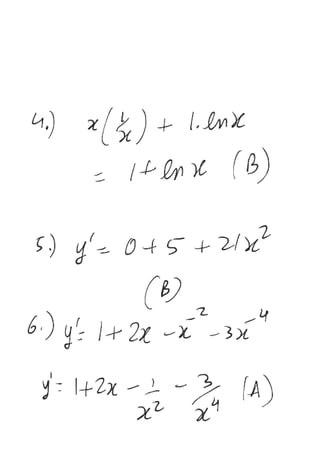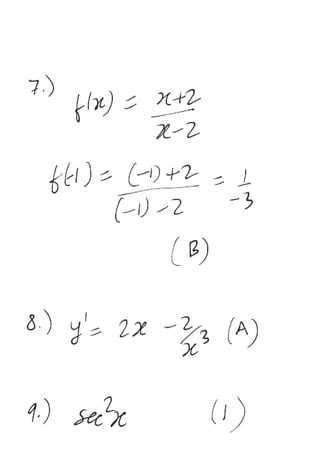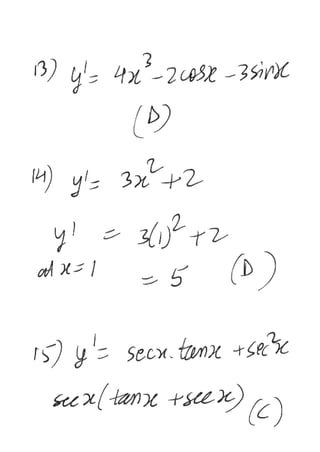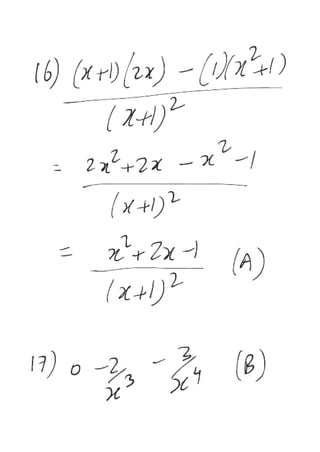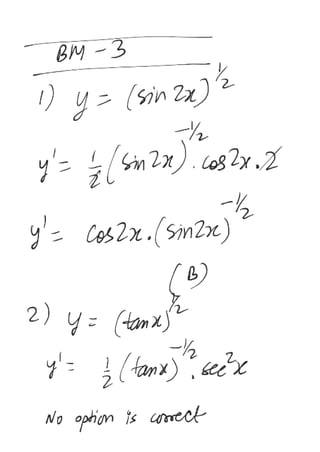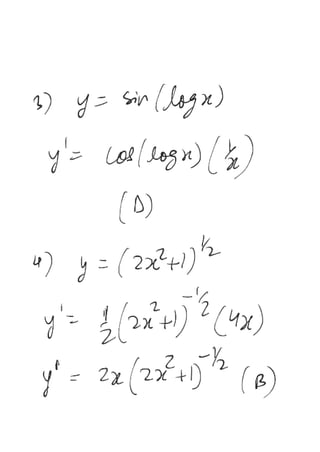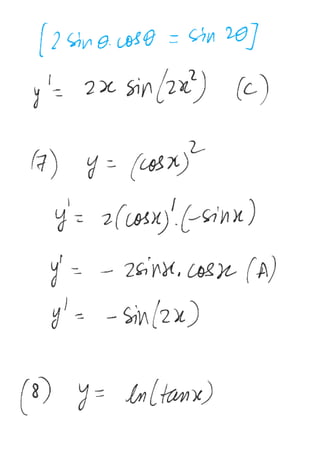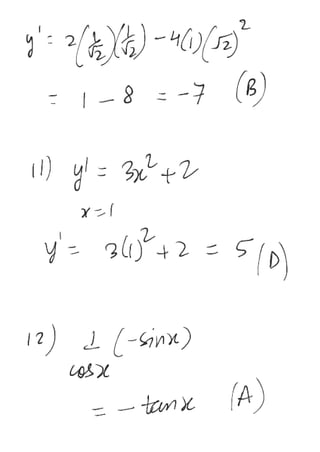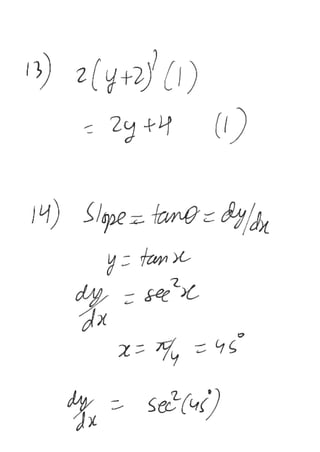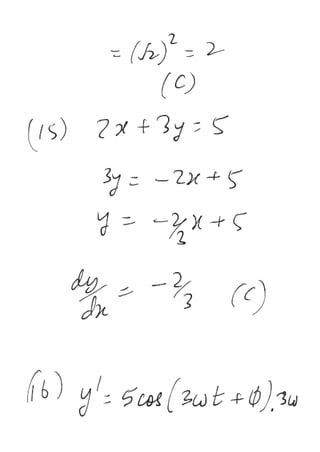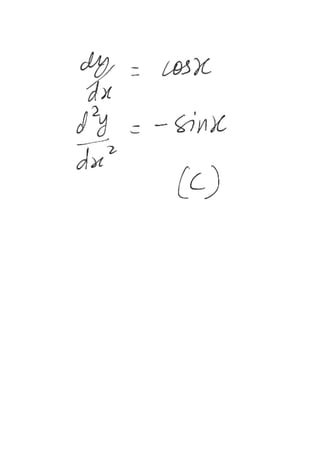The document provides a series of exercises focused on differentiating various mathematical functions with respect to x. It includes examples with polynomial, trigonometric, exponential, and logarithmic functions, along with multiple-choice questions about their derivatives. It also addresses the concepts of slope and double differentiation.

1. Find
dy
dx
of the given functions
1. y = x
n + 2
, where n is constant
2. y = x
3
3. y = x
–n
, where n is constant
4. y = x
–4
5.
1
n
y = x , where n is constant and n 0
z
6.
1
2
y = x
7.
2
3
y = x
"
8. y = ax
3
, where a is a constant
9.
1
4
1
y = x
2
Lakshya Educare
Differentiate with respect to x
a x2
b x4
c x d x9
e x−3
f x−1
g 4x2
h 7x i 2x5
j 3 k 8x−2
l 11x−4
11 (x7/2
)
dx
d
is equal to
(1) x−5/ 2
2
7
(2) x5/2
2
7
−
2
(3)
7
x5/2
(4) x5/2
7
2
12 ⎟
⎠
⎜
⎝ x3
1
dx
d ⎛ ⎞
is equal to
(1)
x4
−3
(2)
3
x2
(3)
3
x2
− (4) 3x2
1
dx
d
(x3/2
) is :
(1)
2
3
x1/2
(2)
2
3
x5/2
(3)
2
3
x7/2
(4)
2
3
x9/2
14 ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
x
1
dx
d
(1)
x
2
1
(2) x (3) –
2x3/2
1
(4)
2x3/2
1
15 The value of
dy
for y = 5x will be -
dx
(A) 5 (B)
2
5x2
(C) zero (D) 10x2
16
dx
d
(πx2
) is equal to
(1) 2πx (2) πx (3) 2x (4)
2
πx
3
PHYSICS
Turtle Tutorials - BM 1
Turtle Tutorials, Marris Road, Aligarh, PH 7617733555 | www.turtletutorials.com

2. 1. If y = x
3
+ 2x
2
+ 7x + 8 then
dx
dy
will be -
(A) 3x2
+ 2x + 15 (B) 3x2
+ 4x + 7 (C) x
3
+ 2x
2
+ 15 (D) x
3
+ 4x + 7
2. If y = x2
sin x , then
dx
dy will be -
(A) x2
cos x + 2x sin x (B) 2x sin x (C) x
2
cos x (D) 2 x cos x
3. If y = ex
. cot x then
dx
dy will be
(A) ex
cot x – cosec2
x (B) e
x
cosec2
x (C) e
x
[cot x – cosec2
x]
(D) e
x
cot x
dx
dy
will be
4. If y = x nx then
(A) nx + x (B) 1 + n x (C) nx (D) 1
dx
dy
5. y = 4 + 5x + 7x3
. Find
(A) 5 - 21x
2
(B) 5 + 21x2
(C) 9 + 7x
2
(D) 5 + 21x
x3
1
x
1
Find
dx
dy
6. y = x +x
2
. +
(A)1 + 2x –
x4
2
3
x
1
(B) 1 + 2x – 4
2
x
(C) 1 – 2x – 4
3
x
(D) 1 + 2x – 3
3
x
7. If f(x) =
x 2
x 2
The value f (–1) is
(A)
3
1
(B)
3
1
(C) 3 (D) –3
8. y = x2
+
x
1
2
.Find
dx
dy
(A) 2x –
x3
2
(B) 2x – 4
2
x
(C) 2x +
x3
2
(D) None of these
2
x
1
2
x
1
2
x
1
Lakshya Educare
PHYSICS
Turtle Tutorials, Marris Road, Aligarh, PH 7617733555 | www.turtletutorials.com

3. )
x
(tan
dx
d
is equal to
(1) sec2
x (2) cotx
(3) – sec2
x (4) – cot x
1
dx
d
(x3
+ 4x2
+ 1) is equal to
(1) c
x
x
3
4
4
x 3
4
+
+
+ (2) 3x2
+ 8x
(3)
4
x4
+ 8x (4) 3x2
+
4
x4
x3
11 ⎟
⎠
⎞
⎜
⎝
⎛
+
+
+ x
tan
x
log
x
1
x
dx
d
(1) 1 –
2
x
1
+ sec2
x
(2) 1 +
x
1
+ sec2
x
(3) 1 +
2
x
1
+
x
1
+ sec2
x
(4) 1 –
2
x
1
+
x
1
+ sec2
x
1
2
x
1
x
dx
d
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+ is equal to
(1)
2
x
1
1+ (2)
2
x
1
1+
−
(3)
2
x
1
1− (4) x2
– 1
1
d
(x4 – 2 sin x + 3 cos x)
dx
(A) 4x3 – 2 cos x + 3 sin x
(B) 3x2 + 2 cosx + 3 sin x
(C) 4x3 + 2 cosx – 3 sin x
(D) 4x3 – 2 cos x – 3 sin x
dy
at x = 1 is -
dx
If
14. y = x3
+ 2x + 1 then
(A) 6 (B) 7
(C) 8 (D) 5
dy
is -
dx
y
15. = secx + tanx , value of
(A) sec2
x + tan x (B) tan2
x + sec x
(C) secx (tanx + secx) (D) sec x (1 + sec x)
dx
d
x 1
(x2
+1)
+
(A) 2
2
(x +1)
x + 2x −1
(B) 2
(x +1)
x2
− 2x +1
(C)
x +1
x2
+ 2x −1
(D) 2
2
(x +1)
x + 2x +1
dx
d
⎟
⎠
⎜
⎝
⎛
+
1+
x3
2
1
x
1 ⎞
(A) x +
x
1
2
+
x3
1
(B)
x 4
3
(C) x –
x
1
2
–
x3
3
(D)
–2
–
x3
–2
–
x x 2
3
16
17.
Lakshya Educare
Turtle Tutorials, Marris Road, Aligarh, PH 7617733555 | www.turtletutorials.com

4. Q.1
dx
d
x
2
sin
(A) (sin 2x)–1/2 (B) cos 2x (sin 2x)–1/2 (C) 2 cos 2x (sin 2x)–1/2 (D) cos 2x (sin 2x)1/2
Q.2
dx
d
x
tan
(A) 2 sec2x (tan x)–1/2 (B)
2
1
sec2x (tan x)–1 (C)
2
1
(tan x)–1/2 (D) 2 (tan x)–1/2
Q.3
dx
d
sin (log x)
(A) cos (log x) (B) log (cos x) (C) x cos (log x) (D)
x
)
x
cos(log
Q.4
dx
d
1
x
2 2
+
(A) 2x (2x2 + 1)1/2 (B) 2x (2x2 + 1)–1/2 (C) (2x2 + 1)1/2 (D) (2x2 + 1)–1/2
Q.5
dx
d x
2
e
(A)
x
2
e x
2
(B) x
2 x
2
e (C) x
2
e (D)
2
/
1
)
x
2
(
e
−
Q.6
dx
d
sin2
(x2
)
(A) 2x sin2
x2
cos x2
(B) 4x sin x2
cos x (C) 2x sin 2x2
(D) 4x sin x cos x2
Q.7 y = cos2
x is given, then
dx
dy
is -
(A) –2 sinx cos x (B) 2 sin x cos x (C) sin2
x (D) none of these
Q.8 If y = log (tanx), then
dx
dy
is -
(A)
x
tan
x
cos2
(B)
x
tan
1
(C)
x
tan
x
sec2
(D) log(sec2
x)
Q.9 If y = sin(2x2
), then
dx
dy
is -
(A) 4x cos (2x2
) (B) 2 cos (2x2
)(C) 4 cos (2x2
) (D) – 4 cos (2x2
)
5
PHYSICS
Lakshya Educare
Turtle Tutorials - BM 3
Turtle Tutorials, Marris Road, Aligarh, PH 7617733555 | www.turtletutorials.com

5. Q.10 If y = sin2
x – 2 tan2
x , then
dx
dy
at x =
4
π
is -
(A) – 11 (B) – 7 (C) – 13 (D) – 15
Q.11 If y = x3
+ 2x + 1 then
dx
dy
at x = 1 is -
(A) 6 (B) 7 (C) 8 (D) 5)
Q.12
dx
d
[log(cosx)] is :
(1) –tan x (2) tan x (3) cot x (4) –cot x
Q.13
dy
d
(y + 2)2
is equal to
(1) 2y + 4 (2) 2y – 4 (3) 4 + y2
(4) 2(y + 1)
14. Slope of graph y = tanx drawn between y and x, at x = is :
4
(A) 0 (B) 1 (C) 2 (D)
2
1
15. Equation of straight line is 2x + 3y = 5. Slope of the straight line is :
(B) 2/3 (C) –2/3 (D) –3/2
(A) 3/2
dt
dy
16. y = 5sin (3 t + )
where and are constant
Find
(A) 15 cos (3 t + )
(C) 15 cos (3 t + )
(B) 15 cos (3 t)
(D) 5 cos (3 t + )
dt
17. If y = e
kt
then
dy
will be
(A) ekt
(B) ekt
/ k (C) tekt
(D) ke
kt
ss
18. Differentiation of sin(x
2
) w.r.t. x is -
(A) cos (x
2
) (B) 2x cos(x
2
) (C) x
2
cos(x
2
) (D) – cos (2x)
19. Double differentiation of displacement w.r.t. time is :
(A) acceleration (B) velocity (C) force (D) none
2
dx
2
If y = x3
then
d y is -
20.
(A) 6x
2
(B) 6x (C) 3x
2
(D) 3x
dx2
d2
y
will be :
21. If y = sinx, then
(A) cos x (B) sin x (C) – sin x (D) sin x + C
Lakshya Educare
Turtle Tutorials, Marris Road, Aligarh, PH 7617733555 | www.turtletutorials.com

6. BM solutions 1,2,3