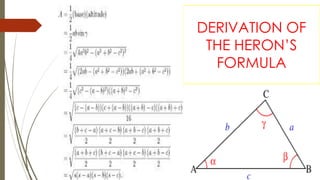
Heron's formula provides a way to calculate the area of a triangle when only the lengths of the three sides are known. It was derived by the Greek mathematician Heron of Alexandria around 10 AD. The formula expresses the area of a triangle in terms of its semiperimeter (s = (a + b + c)/2) and the lengths of its three sides (a, b, c). It can be written as: A = √s(s-a)(s-b)(s-c), where A is the area of the triangle. The document provides an example of using Heron's formula to find the area of an equilateral triangle and discusses applications of the formula.

1. HERON’S FORMULA

2. SELF INTRODUCTION
NAME- Siddhi U Pawar
CLASS- IX Arctic
SUBJECT- Mathematics
TOPIC- Heron’s Formula
CONTENT- 1) Introduction
2) Derivation of the formula
3) Importance of the formula
4) Applications of the formula
5) Summary
SCHOOL- Podar International School, Sangli.

3. INTRODUCTIONWe have studied in the earlier classes about the area of the triangles.
We know that area of a triangle = ½ * base * height.
This formula can be used only when we have the values of base and height
given.
But if length of three sides and one diagonal’s length is given of a triangle then
we need another formula to find the area of the triangle.
Therefore, hero of Alexandria created the formula known as heron’s formula –
Where A is the area of the triangle,
s= semiperimeter i.e. a + b + c / 2 and
a, b, c and the sides of the triangle.

4. WHO DERIVED THIS
FORMULA?
Heron was born in about 10AD
possibly in Alexandria in Egypt.
His works on mathematical and
physical are so numerous and
varied that he was considered
to be an encyclopaedic in
writer in these field.
His geometrical works deal with
problems on mensuration
written in three books.
And in his Book I, he has derived
the famous formula for the area
of the triangle in terms of its
three sides.

5. DERIVATION OF
THE HERON’S
FORMULA

6. FORMULA FOR EQUILATERAL
TRIANGLE
Let the side of the equilateral triangle be ‘a’.
S = ½ (a + a + a) = 3/2 a
A = √ s (s – a) (s – b) (s – c)
= √ 3/2 a (3/2 a – a) (3/2 a – a) (3/2 a – a)
= √ 3/2a (a/2) (a/2) (a/2)
= √ 3 * a2 * a2/ 22 * 22
= a * a/4 √3
= a2/4 √3
= √3/4 a2

7. IMPORTANCE OF THIS FORMULA
There are just many figures that
specifies the lengths and their
area is to be found. Sometimes
on the basis of perimeter just we
need to find the area. All the
types of triangles can find their
area with this formula.
Also sometimes quadrilaterals are
bisected and their area is to be
found. At that same time we can
use this heron’s formula. We
should first divide the
quadrilateral and then we should
find the area. All quadrilaterals’
area can be found by this
formula.

8. APPLICATIONS OF THE FORMULA
This formula is very useful so now let see its application
Here cloth which is used, its
area can be calculated by
heron’s formula
To calculate the small
triangular shaped
umbrella design etc.

9. APPLICATIONS OF THE FORMULA
This formula is very helpful where it is not possible to find the
height of a triangle.
We can find the area of small
triangles in wheel toys
We can find area of the
quadrilaterals by dividing it
into the triangles

10. PROBLEMS ON FORMULA
Q.There is a slide in a park. One of its side walls has been
painted in some colour with a message ‘KEEP THE PARK
GREEN AND CLEAN’ (See fig). If the sides of the wall ae
15m, 11m and 6m, find the area painted in colour.
ANS. =
a = 15m, b = 11m, c = 6m.
A = √ s (s – a) (s – b) (s – c)
= √16 (16 – 15) (16 – 11) (16 – 6) m2
= √16 * 1 * 5 * 10 m2
= √2 * 400 m2
= 20 √2 m2
Thus, the required area painted in colour = 20 √2 m2

11. PROBLEMS ON FORMULA
Q. Find the area of a quadrilatersl ABCD in which AB = 3cm, BC = 4cm, CD =
4cm, DA = 5cm and AC = 5cm.
ANS.=
Area of ABC tri. = 6 cm2
Area of ACD tri. = 9.2 cm2
Thus, area of ABCD = 6 + 9.2 = 15.2 cm2

12. SUMMARY
Area of a triangle with its side as a, b and
c is calculated by using heron’s formula –
where s = a + b + c / 2.
Area of a quadrilateral whose sides and
one diagonal are given, can be
calculated by dividing the quadrilateral
into two triangles and using the Heron’s
formula.