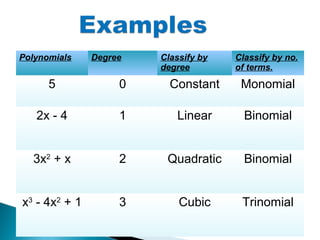
The document provides an overview of algebraic expressions and polynomials, including definitions of terms such as constants, variables, degrees, and types of polynomials like linear, quadratic, and cubic. It also explains the remainder theorem and includes examples of various algebraic identities. Additionally, it classifies polynomials based on their degree and number of terms.

1. Mathematics
Class: IX

2. Algebraic Expression: In mathematics, an algebraic expression is
an expression built up from integer constants, variables, and
the algebraic operations (addition, subtraction, multiplication,
division and exponentiation by an exponent that is a rational number).
e.g.- (a) 2x3
– 4x2
+ 6x – 3 is a polynomial in one variable x.
(b) 8p7
+ 4p5
+ 11p3
- 9p is a polynomial in one variable p.
(c) 4 + 7x4/5
+ 9x5
is an expression but not a polynomial
since it contains a term x4/5
, where 4/5
is not
a non-negative integer.

3. Polynomials: An algebraic expression in which the variable
involved have only non-negative integral powers is called a
polynomial.
e.g.: 3x2
+ 4y
Constants: A symbol having a fixed numerical value is called a
constant.
e.g.: In polynomial 3x2
+ 4y, 3 and 4 are the constants.
Variables: A symbol which may be assigned different
numerical values is called as a variables.
e.g.: In polynomial 3x2
+ 4y, x and y are the variables.

4. Degree: The highest power of a variable in the polynomial is
called degree of that polynomial.
e.g.: 5x2
+ 3, here the degree is 2.
Constant Polynomial: A polynomial containing one term only,
consisting of a constant is called a constant polynomial.
The degree of a non-zero constant polynomial is zero.
e.g.: 3, -5, 7/8 etc. are all constant polynomials.
Zero Polynomial: A polynomial consisting one term only,
namely zero only, is called a zero polynomial.
The degree of a zero polynomial is not defined.

5. Like Terms: two or more having same type of variable and same
power on them are said to be like terms for example 3x , -7/2x,
8/9x , are like terms.
Unlike Terms: terms if they are not like then they are known as
unlike terms for example 7a , 8b , 19/3c are unlike terms.

6. Monomial: Algebraic expression that consists only one term is
called monomial. e.g.: 3x2
, 4y
Binomial: Algebraic expression that consists two terms is called
binomial. e.g.: 3x2
- 8y2
, x2
- 4
Trinomial: Algebraic expression that consists three terms is
called trinomial. e.g.: z2
+ 4z - 9
Polynomial: Algebraic expression that consists many terms is
called polynomial. e.g.: 3x3
+ 4x2
- 2x - 7

7. Types of polynomial on the basis of degree are :
Linear polynomial: A polynomial of degree 1 is called a linear
polynomial. e.g.: 3x, 4y
Quadratic polynomial: A polynomial of degree 2 is called a
quadratic polynomial. e.g.: x2
+ 5, y2
- 9
Cubic polynomial : A polynomial of degree 3 is called a cubic
polynomial. e.g.: x3
- x2
+ 5x - 7
Bi-quadratic polynomial : A polynomial of degree 4 is called
a bi-quadratic polynomial. e.g.: 3x4
- x3
+ x2
+ 5x - 7

8. Polynomials Degree Classify by
degree
Classify by no.
of terms.
5 0 Constant Monomial
2x - 4 1 Linear Binomial
3x2
+ x 2 Quadratic Binomial
x3
- 4x2
+ 1 3 Cubic Trinomial

9. How to convert a polynomial into standard
form?
OR

10. Let f(x) be a polynomial of degree n > 1 and let a be any real number.
When f(x) is divided by (x-a) , then the remainder is f(a).
PROOF Suppose when f(x) is divided by (x-a), the quotient is g(x) and the remainder
is r(x).
Then, degree r(x) < degree (x-a)
degree r(x) < 1 [ therefore, degree (x-a)=1]
degree r(x) = 0
r(x) is constant, equal to r (say)
Thus, when f(x) is divided by (x-a), then the quotient is g(x) and the remainder is r.
Therefore, f(x) = (x-a) x g(x) + r (i)
Putting x=a in equation (i), we get r = f(a)
Thus, when f(x) is divided by (x-a), then the remainder is f(a).

11. Let f(x) be a polynomial of degree n>1 and let a be
any real number. If f(a) = 0 then (x-a) is a factor of f(x).
Proof: Let f(a) = 0
On dividing f(x) by (x-a), let g(x) be the quotient.
Also, by remainder theorem, when f(x) is divided by (x-a), then the
remainder is f(a).
Therefore, f(x) = (x-a) x g(x) + f(a)
f(x) = (x-a) x g(x) as f(a)=0 (given)
(x-a) is a factor of f(x).

12.  (a + b)2
= a2
+ 2ab + b2
 (a – b)2
= a2
– 2ab + b2
 a2
– b2
= (a - b) (a – b)
 (x + a) (x + b) = x2
+ (a + b)x + ab
 (a + b + c)2
= a2
+ b2
+ c2
+ 2ab + 2bc + 2ca
 (a + b)3
= a3
+ b3
+ 3ab (a + b)
 (a – b)3
= a3
– b3
– 3ab (a – b)
 a3
+ b3
= (a + b) (a2
– ab + b2
)
 a3
– b3
= (a – b) (a2
+ ab + b2
)
 a3
+ b3
+ c3
– 3abc = (a + b + c) (a2
+ b2
+ c2
– ab – bc – ca)
 a3
+ b3
+ c3
= 3abc , If a + b + c = 0

13. THANKS