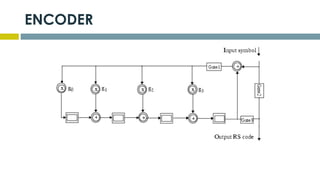
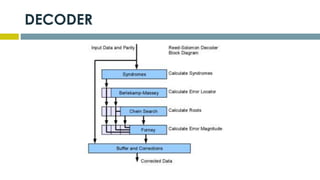
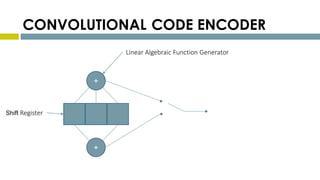
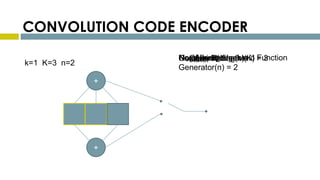
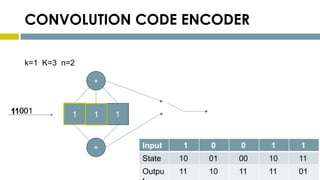
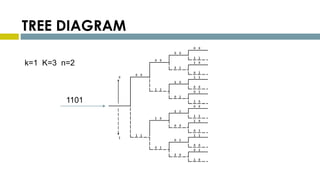
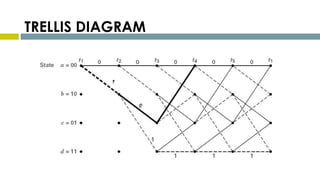
This document provides an overview of Reed-Solomon codes and convolutional codes. It describes the key properties and components of Reed-Solomon codes, including how they encode messages by dividing them into blocks and adding redundancy. It also explains convolutional codes use shift registers and linear algebraic functions to encode redundant information. The document compares block and convolutional codes and discusses factors like coding rate and constraint length that impact their performance.

1. REED SOLOMON CODE
AND CONVOLUTION
CODE

2. REED SOLOMON
CODE

3. CONTENTS
 Introduction
 Properties of RS code
 RS Encoder
 RS Decoder
 Software Implementation
 Advantages
 Disadvantages
 Applications

4. INTRODUCTION
 Reed–Solomon codes are an important group of error-correcting codes introduced
by Irving S. Reed and Gustave Solomon in 1960.
 RS codes operate on the information by dividing the message stream into blocks of
data, adding redundancy per block depending only on the current inputs.
 It is capable to correct both burst errors (where a series of bits in the codeword are
received in error) and erasures.

5. PROPERTIES OF RS CODE
 RS codes are generally represented as RS (n, k), with s-bit symbols.
 Block Length: n
No. of Original Message symbols: k
Number of Parity Digits: n – k
 A Reed-Solomon decoder can correct up to t symbols that contain errors in a
codeword, where 2t = n-k.
 The relationship between the symbol size, m, and the size of the codeword n, is
given by n=2s-1

6.  The following diagram shows a typical Reed-Solomon codeword:
k 2t
n
Data Parity

7. Example:-
 RS(255,223) with 8-bit symbols.
 Each codeword contains 255 code word bytes, of which 223 bytes are data and 32
bytes are parity. For this code:
n = 255, k = 223, s = 8
2t = 32, t = 16
 The decoder can correct any 16 symbol errors in the code word: i.e. errors upto 16
bytes anywhere in the codeword can be automatically corrected.

8.  Given a symbol size s, the maximum codeword length (n) for a Reed-Solomon code
is n = 2s – 1
 For example, the maximum length of a code with 8-bit symbols (s=8) is 255 bytes.
 Reed-Solomon codes may be shortened by (conceptually) making a number of data
symbols zero at the encoder, not transmitting them, and then re-inserting them at
the decoder.

9.  Example: The (255,223) code described above can be shortened to (200,168). The
encoder takes a block of 168 data bytes, (conceptually) adds 55 zero bytes, creates
a (255,223) codeword and transmits only the 168 data bytes and 32 parity bytes.

10. ENCODER

11.  Message Polynomial-
c(x) = m(x). xn-k
 RS generator Polynomial-
g(x) = g0 + g1. x+ g2 x2+ …. + g2t-1. x2t-1 + x2t

12. DECODER

13. SOFTWARE IMPLEMENTATION
 Until recently, software implementations in real-time required too much
computational power for all but the simplest of Reed-Solomon codes (i.e. codes
with small values of t).
 The following Table gives some example benchmark figures on a 166 MHz Pentium
PC:
Code Data rate
RS(255,251) 12 Mb/s
RS(255,239) 2.7 Mb/s
RS(255,223) 1.1 Mb/s

14. ADVANTAGES
 Reed-Solomon codes are most widely used to correcting burst errors.
 Coding gain is very high.
 The Coding rate is very high for Reed Solomon code so it is suitable for many
applications including storage and transmission.

15. DISADVANTAGES
 Unlike BCH codes , RS Codes does not perform considerably well in BPSK
modulation schemes.
 Bit Error Ratio(BER) for Reed-Solomon Codes is not as good as BCH codes.

16. APPLICATIONS
 Data Storage
 Bar Code
 Satellite Broadcasting
 Spread-Spectrum System
 Ultra Wideband(UWB)

17. CONVOLUTION CODE

18. ERROR CORRECTION CODE
 There are four important error correction codes that find applications in digital
transmission. They are :
18
Block Parity
Hamming Code
Interleaved Code
Convolutional Code

19. INTRODUCTION
 Convolutional codes are introduced in 1955 by Elias.
 Convolution coding is a popular error-correcting coding method used in
digital communications. A message is convoluted, and then transmitted
into a noisy channel.
 This convolution operation encodes some redundant information into
the transmitted signal.
19

20. CONVOLUTIONAL ENCODER
 Convolutional encoding of data is accomplished using a shift register
and associated combinatorial logic that performs modulo-two addition.
 A shift register is merely a chain of flip-flops.

21. PARAMETERS OF CONVOLUTION ENCODER
 Convolutional codes are commonly specified by three parameters:
 n = number of output bits
 k = number of input bits
 K = number of shift registers
 Code Rate: The quantity k/n is called as code rate. It is a measure of the efficiency
of the code.
 Constraint Length: The quantity L(or K) is called the constraint length of the code. It
represents the number of bits in the encoder memory that affect the generation of
the n output bits.

22. CONVOLUTIONAL CODE ENCODER
+
+
Shift Register
Linear Algebraic Function Generator

23. CONVOLUTION CODE ENCODER
+
+
Constraint Length (K) = 3Code Rate = k/nNo of input bits (k)= 1state = K-1state = 2k=1 K=3 n=2
No of linear Algebraic Function
Generator(n) = 2

24. CONVOLUTION CODE ENCODER
+
0 0 0
+
11001
k=1 K=3 n=2
Input 1 0 0 1 1
State 10 01 00 10 11
Outpu 11 10 11 11 01
1 1 111100110111 1

25. REPRESENTATION OF CONVOLUTION CODES
 State Diagram
 Tree Diagram
 Trellis Diagram

26. STATE DIAGRAM
 Contents of shift registers make up "state" of code:
 Most recent input is most significant bit of state.
 Oldest input is least significant bit of state.
 (this convention is sometimes reverse)

27. TREE DIAGRAM
1101
k=1 K=3 n=2

28. TRELLIS DIAGRAM REPRESENTATION
 The trellis diagram is basically a redrawing of the state diagram. It
shows all possible state transitions at each time step. Then we connect
each state to the next state.
 There are only two choices possible at each state. These are
determined by the arrival of either a 0 or a 1 bit.
 The arrows show the input bit.
 The arrows going upwards represent a 0 bit and going downwards
represent a 1 bit.

29. TRELLIS DIAGRAM

30. DIFFERENCE BETWEEN BLOCK CODE AND CONVOLUTION
CODE
 The difference between block codes and convolution codes is the encoding
principle.
 In the block codes, the information bits are followed by the parity bits while in
convolution codes the information bits are spread along the sequence.
 The block codes can be applied only for the block of data whereas convolution
coding can be applied to a continuous data stream as well as to blocks of data.

31. ADVANTAGES
 Convolution coding is a popular error-correcting coding method used in digital
communications.
 The convolution operation encodes some redundant information into the
transmitted signal.
 It is simple and has good performance with low implementation cost.

32. FACTORS AND PROPERTIES
 The performance of a convolutional code depends on the coding rate and the
constraint length.
 Longer constraint length K
More powerful code
More coding gain
 Smaller coding rate R=k/n
More powerful code due to extra redundancy
Less bandwidth efficiency

33. THANK YOU
E047 E048 E049 E050 E056 E058CREATED