Il documento tratta della derivata di una funzione e della sua definizione in un punto, spiegando il concetto di retta tangente rispetto alla retta secante. Viene introdotto il limite del rapporto incrementale, illustrando come questo porti alla definizione della derivata e alla distinzione tra derivata destra e sinistra. Infine, si evidenzia il significato geometrico della derivata come coefficiente angolare della retta tangente al grafico della funzione.

1. DERIVATADERIVATA
DI UNA FUNZIONEDI UNA FUNZIONE

2. Il problema da cui partiamo: la ricerca della
retta TANGENTE al grafico di una funzione
?...ma non lo sappiamo già fare?
∆=0 in quale contesto?
In generale secante/tangente

3. SIGNIFICATO GEOMETRICO DELLA DERIVATASIGNIFICATO GEOMETRICO DELLA DERIVATA
O x1 x2 x
y
Promemoria:
Il coefficiente angolare di una retta passante
per i due punti P1(x1,y1) e P2(x2,y2) è :
12
12
xx
yy
m
−
−
= y1
y2
.
.
P1
P2
Data una funzione f(x), il rapporto
incrementale relativo al punto x0 : y
f(x0)
f(x0+h)
.
.
O x0 x0+h x
h
)f(xh)f(x 00 −+
( ))f(x,x 00
risulta essere il coefficiente angolare
della retta passante per i punti:
( )h)f(x,hx 00 ++
Questa retta la chiameremo retta secante
passante per il punto di ascissa x0
retta secante

4. O x
y
f(x0)
x0
.
h
.
h
.
h
f(x0+h)
x0+h
.
h
Quando h→0
accade che:
la retta secante tende l
alla retta
tangente
analogamente a quanto
accade al concetto di
velocità media che
diventa la velocità
istantanea
retta
tangente
.
retta secante

5. DEFINIZIONE DI DERIVATA DI UNA FUNZIONE IN UN PUNTODEFINIZIONE DI DERIVATA DI UNA FUNZIONE IN UN PUNTO
O x
y
f(x0)
f(x0+h)
∆x = h
∆f
Consideriamo una funzione f(x)
definita in un intervallo ( a, b )
Sia x0 un punto interno ad (a, b
) e sia x0 + h il punto
ottenuto aggiungendo ad x0 la
quantità hSiano
∆f = f(x0+h) – f(x0)
∆x = x0+h – x0 = h
Chiameremo infine rapporto incrementale relativo al punto x0
e all’incremento h il seguente rapporto:
sec
00
h
)f(xh)f(x
Δx
Δf
m=
−+
=
e le chiameremo rispettivamente incremento della funzione (∆f )
e incremento della variabile (∆x = h)
a b
.
x0
.
x0+h

6. Definizione: derivata di y= f(x) in un puntoDefinizione: derivata di y= f(x) in un punto
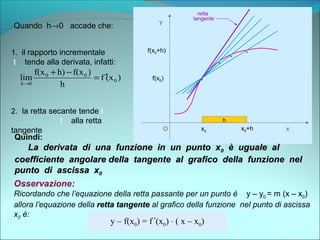
Diremo derivata della f(x) nel punto x0 il risultato del limite
tg
h
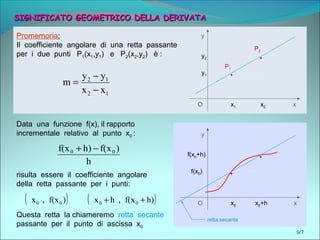
m=
−+
→ h
)f(xh)f(x
lim 00
0
e lo indicheremo con uno qualunque dei simboli:
f ’(x0) y ’(x0) ( )[ ] 0xxxDf =
)x(x 0
dx
df
=
derivata in simboli:
h
)f(xh)f(x
lim)(x'f 00
0
0
−+
=
→h

7. 7/7
Definizione:Definizione: funzione derivabile in un puntofunzione derivabile in un punto
Una funzione si dice derivabile in un punto xUna funzione si dice derivabile in un punto x00 se esiste ed è finitose esiste ed è finito il limiteil limite
del rapporto incrementale della funzione quando l’incremento h della variabiledel rapporto incrementale della funzione quando l’incremento h della variabile
tende a zero, cioètende a zero, cioè se esiste ed è finitose esiste ed è finito il seguente limite:il seguente limite:
Se il precedente limite non esiste, oppure non dà come risultato un numeroSe il precedente limite non esiste, oppure non dà come risultato un numero
finito, allora diremo che la funzione f(x) non è derivabile nel puntofinito, allora diremo che la funzione f(x) non è derivabile nel punto xx00
Se il precedente limite non esiste, oppure non dà come risultato un numeroSe il precedente limite non esiste, oppure non dà come risultato un numero
finito, allora diremo che la funzione f(x) non è derivabile nel puntofinito, allora diremo che la funzione f(x) non è derivabile nel punto xx00
h
)f(xh)f(x
lim 00
0
−+
→h

8. 8/7
DERIVATA DESTRA E DERIVATA SINISTRADERIVATA DESTRA E DERIVATA SINISTRA
Certe volte, pur non esistendo il limite per h→0 del rapporto incrementale,
possono esistere finiti il limite destro e/o il limite sinistro:
h
)f(xh)f(x
lim 00
0
−+
+
→h h
)f(xh)f(x
lim 00
0
−+
−
→h
Allora possiamo dare la seguente:
Definizione: derivata destra e derivata sinistra
Diremo derivata destra e derivata sinistra di f(x) in x0 , e le indicheremo con i
simboli e i risultati, se esistono e sono finiti , dei seguenti
limiti:
h
)f(xh)f(x
lim)(xf 00
0
0
−+
=′ +
→
+
h h
)f(xh)f(x
lim)(xf 00
0
0
−+
=′ −
→
−
h
)(xf 0−
′)(xf 0+
′
Osservazione:Osservazione:
Quando una funzione è derivabile in xQuando una funzione è derivabile in x00 nel senso della definizione ordinarianel senso della definizione ordinaria
allora esistono anche la derivata destra e quella sinistra eallora esistono anche la derivata destra e quella sinistra e sono uguali fra lorosono uguali fra loro
Osservazione:Osservazione:
Quando una funzione è derivabile in xQuando una funzione è derivabile in x00 nel senso della definizione ordinarianel senso della definizione ordinaria
allora esistono anche la derivata destra e quella sinistra eallora esistono anche la derivata destra e quella sinistra e sono uguali fra lorosono uguali fra loro

9. 9/7
SIGNIFICATO GEOMETRICO DELLA DERIVATASIGNIFICATO GEOMETRICO DELLA DERIVATA
O x1 x2 x
yPromemoria:
Il coefficiente angolare di una retta passante
per i due punti P1(x1,y1) e P2(x2,y2) è :
12
12
xx
yy
m
−
−
=
y1
y2
.
.
P1
P2
Data una funzione f(x), il rapporto
incrementale relativo al punto x0 : y
f(x0)
f(x0+h)
.
.
O x0 x0+h x
h
)f(xh)f(x 00 −+
( ))f(x,x 00
risulta essere il coefficiente angolare
della retta passante per i punti:
( )h)f(x,hx 00 ++
Questa retta la chiameremo retta secante
passante per il punto di ascissa x0
retta secante

10. O x
y
f(x0)
x0
.
h
.
h
.
h
f(x0+h)
x0+h
.
h
Quando h→0 accade che:
2. la retta secante tende l
l alla retta
tangente
1. il rapporto incrementale
t tende alla derivata, infatti:
)(xf
h
)f(xh)f(x
lim 0
00
0
′=
−+
→h
Quindi:Quindi:
La derivata di una funzione in un punto xLa derivata di una funzione in un punto x00 è uguale alè uguale al
coefficiente angolare della tangente al grafico della funzione nelcoefficiente angolare della tangente al grafico della funzione nel
punto di ascissa xpunto di ascissa x00
Osservazione:
Ricordando che l’equazione della retta passante per un punto è y – y0 = m (x – x0)
allora l’equazione della retta tangenteretta tangente al grafico della funzione nel punto di ascissa
x0 è:
y – f(x0) = f ’(x0) ⋅ ( x – x0)
retta
tangente
.
retta secante