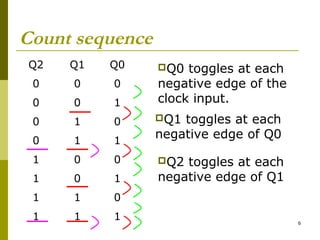
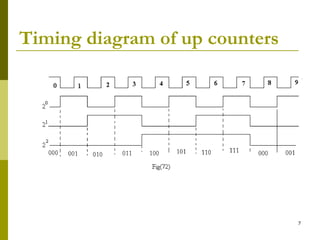
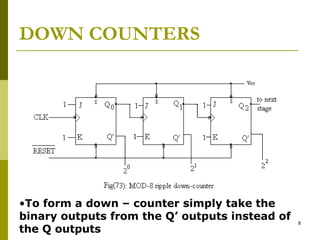
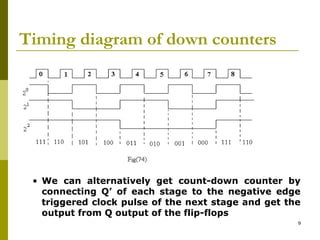
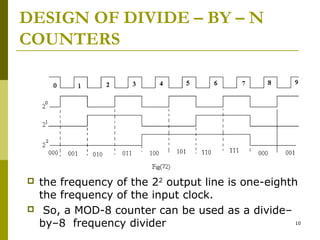
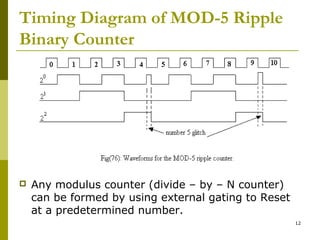
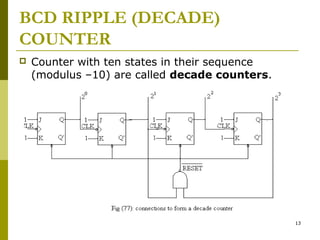
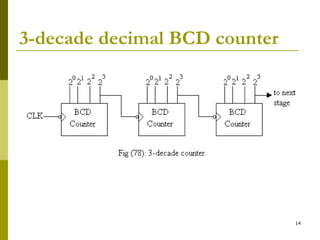
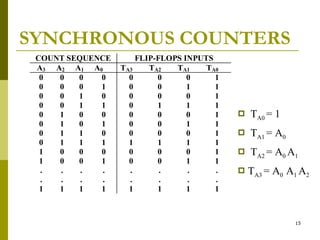
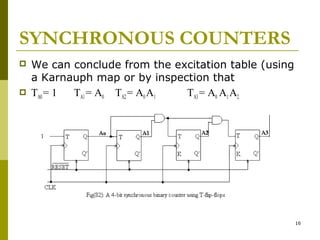
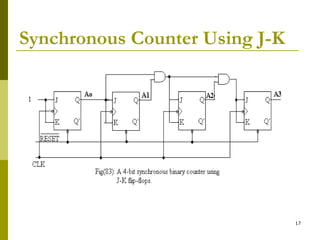
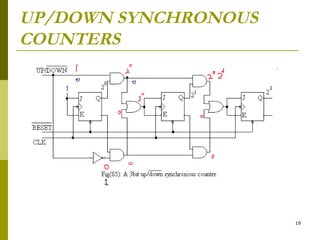
This document discusses different types of counters. It begins by classifying counters as either asynchronous (ripple) or synchronous. It then describes binary, decimal, octal and special counters based on their counting sequences. The document provides examples of 3-bit asynchronous and synchronous up/down counters. It explains how to create divide-by-N counters using MOD-N ripple counters. BCD ripple counters and 3-decade decimal counters are also illustrated. Finally, the timing and operation of synchronous counters is examined along with synchronous down and up/down counters.

1. CHAPTER 8
Counter Circuits
1

2. CLASSIFICATION OF
COUNTERS

Asynchronous (ripple)


They use the O/P of one FF to generate
the clock transition on another FF (s)
Synchronous

clock inputs on each FF are connected
together
2

3. CLASSIFICATION OF
COUNTERS

Binary

0,1,2, ….,2n –1



0,1,2, …, 10n ‑ 1


i- 0,1, …. 9
ii- 0,1, …99
10 states
100 states
Octal


22 states
24 states
Decimal


i- 0,1,2,3
ii- 0,1,…,15
0,1,2, .. , 8n-1
Special

Any specified sequence sf states
3

4. CLASSIFICATION OF
COUNTERS
up
 down
 up/down

4

5. 3-bit Asynchronous Binary counter :
(Mod-8)
5

6. Count sequence
Q2
Q1
Q0
0
0
0
0
0
1
toggles at each
negative edge of the
clock input.
0
1
0
Q1
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Q0
toggles at each
negative edge of Q0
Q2
toggles at each
negative edge of Q1
6

7. Timing diagram of up counters
7

8. DOWN COUNTERS
•To form a down – counter simply take the
binary outputs from the Q’ outputs instead of
the Q outputs
8

9. Timing diagram of down counters
• We can alternatively get count-down counter by
connecting Q’ of each stage to the negative edge
triggered clock pulse of the next stage and get the
output from Q output of the flip-flops
9

10. DESIGN OF DIVIDE – BY – N
COUNTERS


the frequency of the 22 output line is one-eighth
the frequency of the input clock.
So, a MOD-8 counter can be used as a divide–
10
by–8 frequency divider

11. A MOD-5 Ripple Binary Counter

the number 5 will appear at the outputs for a short
duration, just long enough to Reset the flip-flops. The
resulting short pulse on the 20 line is called a glitch.
11

12. Timing Diagram of MOD-5 Ripple
Binary Counter

Any modulus counter (divide – by – N counter)
can be formed by using external gating to Reset
at a predetermined number.
12

13. BCD RIPPLE (DECADE)
COUNTER

Counter with ten states in their sequence
(modulus –10) are called decade counters.
13

14. 3-decade decimal BCD counter
14

15. SYNCHRONOUS COUNTERS
COUNT SEQUENCE
A3 A2 A1 A0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
.
.
.
.
.
.
.
.
1
1
1
1
FLIP-FLOPS INPUTS
TA3
TA2
TA1
TA0
0
0
0
1
0
0
1
1
0
0
0
1
0
1
1
1
0
0
0
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
0
1
0
0
1
1
.
.
.
.
.
.
.
.
1
1
1
1

TA0 = 1

TA1 = A0

TA2 = A0 A1

TA3 = A0 A1 A2
15

16. SYNCHRONOUS COUNTERS


We can conclude from the excitation table (using
a Karnauph map or by inspection that
TA0 = 1
TA1 = A0 TA2 = A0 A1
TA3 = A0 A1 A2
16

17. Synchronous Counter Using J-K
17

18. SYNCHRONOUS BINARY DOWNCOUNTER
• The only change is that the outputs are used as inputs to
the T (or J–K) input of the next flip-flop.
18

19. UP/DOWN SYNCHRONOUS
COUNTERS
19