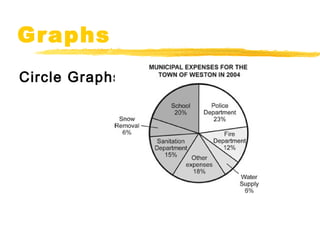
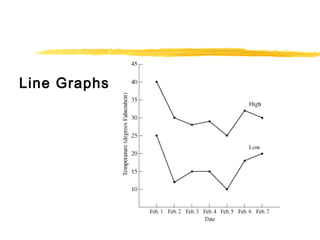
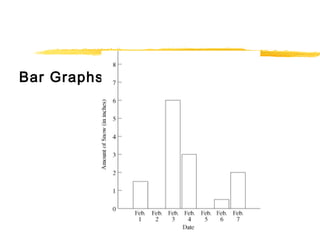
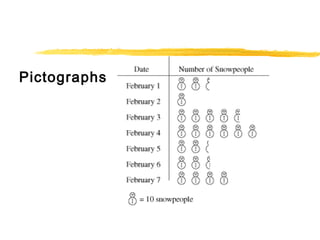
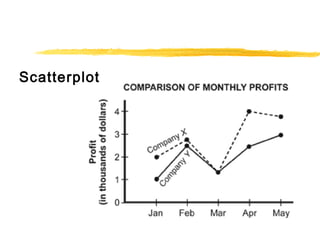
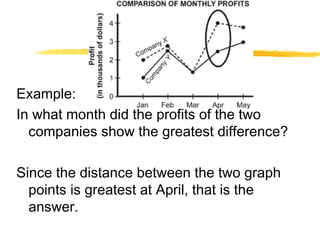
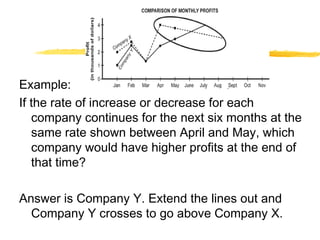
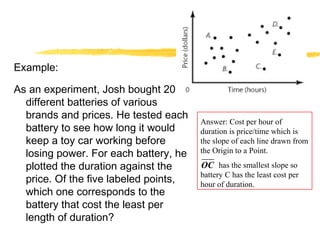
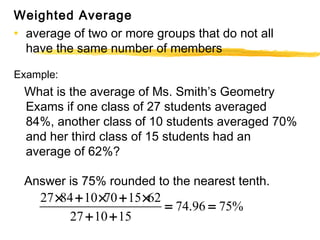This document provides an overview of topics related to data analysis, statistics, and probability that may be covered on the SAT. It includes brief explanations of different types of graphs used to display data, guidelines for interpreting data from graphs, tables, and charts, definitions and examples of common statistical concepts like mean, median, mode, and weighted average, and explanations of probability, independent and dependent events, and calculating probabilities using geometric models. Practice problems with solutions are provided as examples.

1. Data Analysis, Statistics,
and Probability Review
The SAT doesn’t include
computation of standard deviation

2. Data Interpretation
• interpret information in graphs, tables, or
charts
• then compare quantities, recognize trends
and changes in the data
• perform calculations based on the
information you have found

3. Graphs
Circle Graphs

4. Line Graphs

5. Bar Graphs

6. Pictographs

7. Scatterplot

8. Data Interpretation
Questions
When working with data interpretation questions:
• Look at the graph, table, or chart to make sure
you understand it.
• Make sure you know what type of information is
being displayed.
• Read the labels.
• Make sure you know the units.
• Make sure you understand what is happening to
the data as you move through the table, graph,
or chart.
• Read the question carefully.

9. Example:
In what month did the profits of the two
companies show the greatest difference?
Since the distance between the two graph
points is greatest at April, that is the
answer.

10. Example:
If the rate of increase or decrease for each
company continues for the next six months at the
same rate shown between April and May, which
company would have higher profits at the end of
that time?
Answer is Company Y. Extend the lines out and
Company Y crosses to go above Company X.

11. Example:
As an experiment, Josh bought 20
different batteries of various
brands and prices. He tested each
battery to see how long it would
keep a toy car working before
losing power. For each battery, he
plotted the duration against the
price. Of the five labeled points,
which one corresponds to the
battery that cost the least per
length of duration?
Answer: Cost per hour of
duration is price/time which is
the slope of each line drawn from
the Origin to a Point.
has the smallest slope so
OC
battery C has the least cost per
hour of duration.

12. Statistics
Arithmetic Mean
• average
•
sum of list of values
number of values in list
Median
• middle value of a list when the numbers are in
order
Mode
• value or values that appear the greatest number of
times

13. Weighted Average
• average of two or more groups that do not all
have the same number of members
Example:
What is the average of Ms. Smith’s Geometry
Exams if one class of 27 students averaged
84%, another class of 10 students averaged 70%
and her third class of 15 students had an
average of 62%?
Answer is 75% rounded to the nearest tenth.
´ + ´ + ´ = =
27 84 10 70 15 62 74.96 75%
+ +
27 10 15

14. Average of Algebraic Expressions
• also called arithmetic mean
Example:
Find the arithmetic mean of 3x+4 and 5x -10.
Answer:
x + + x - = x - = x -
3 4 5 10 8 6 4 3
2 2

15. Using Averages to Find Missing Numbers
• average =
sum of list of values
number of • therefore, average ´
values in list number of values = sum of
values
Example:
Sean has test scores of 88, 83, 72 and 90.
What does he need to make on his fifth test
to have an 85 average?
Answer:
85 x 5 = 425 88 + 83 +72 +90 = 333
425 – 333 = 92

16. Probability
Probability of Event
• number between 0 and 1, inclusive
• if an event is certain, it has probability 1
• if an event is impossible, it has probability 0
Independent Events
• the outcome of either event has no effect on the
other
• to find the probability of two or more independent
events occurring together, multiply the
probabilities of the individual events

17. Dependent Events
• the outcome of one event affects the
probability of another event
• use logical reasoning to help figure out
probabilities involving dependent events

18. Geometric Probability
• Probability involving geometric figures
Example: Given the large circle has
radius 8 and the small circle has
radius 2. If a point is chosen at
random from the large circle, what is
the probability that the point chosen
will be in the small circle?
p ´(8)2 = 64p
Answer: Area of large circle =
Area of small circle =
p ´(2)2 = 4p
So the probability of the point being in the small circle
is .
p
p
4 =
1
64 16

19. Example:
A game at the state fair has a circular target with a
radius of 10.7 cm on a square board measuring
30 cm on a side. Players win prizes if they
throw a dart and hit the circular area only. What
is the probability of winning with one throw of a
dart?
measure of geometric model representing
P(E) = desired outcomes in the event
measure of geometric model representing
all outcomes in the same space

20. Solution:
Area of circle A =
Area of entire square board A =
p (10.7)2 = 359.7
302 = 900
359.7 .40
900
P (E) = =
or 40% chance of hitting in the
circle.