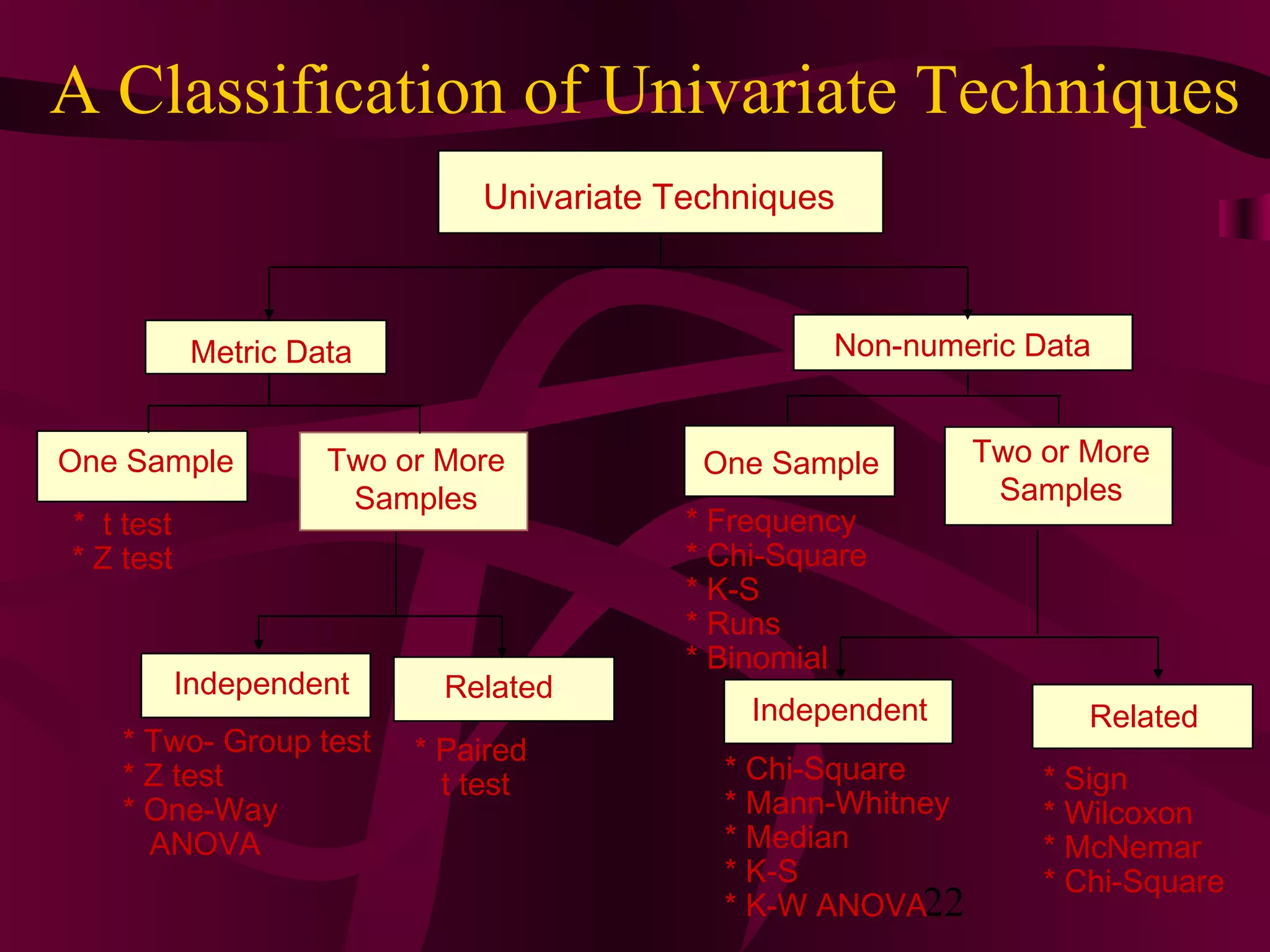
This document discusses various statistical analysis techniques used in marketing research. It begins by explaining how to bring raw data into order through arrays, tabulations and establishing categories. It then discusses descriptive, inferential, differences, associative and predictive analysis. The document also covers univariate techniques like t-tests, z-tests, ANOVA, chi-square tests and multivariate techniques like regression, conjoint analysis and cluster analysis. It provides guidance on when to use specific statistical tests and covers statistics used in cross-tabulation like phi coefficient, contingency coefficient and Cramer's V.

1. 1
DATA ANALYSIS
AND
INTERPRETATION

2. 2
SOME PROBLEMS OF
UNDERSTANDING
• This slide is dedicated to those who feel any
discussion of mathematics or statistics with a
feeling of withdrawal.
• A few statements are given on the next two
slides, acceptance of which may reduce such
apprehensions so that they will not interfere
with increasing one’s research ability with
regard to analytical tools.

3. 3
FOLLOWING STATEMENTS ARE
TRUE
• Sheer unfamiliarity with mathematical
language presents a serious obstacle that
disappears as one employs it.
• Mathematical expressions are simply an
alternative to verbal ones. They are much
more efficient in being able to say quickly in
numbers and nonverbal symbols what would
require many words.

4. 4
• Mathematical expressions are clear and
specific. They avoid ambiguities that obscure
our verbal communication.
• Numbers and formulas are abstractions and
thus should offer no inherent confusions.
• If you regard quantitative analytical methods
as possible keys to unlock the meaning of data
and expand your interpretive powers, you will
welcome their assistance and adopt a positive
attitude towards them.

5. 5
NATURE AND FUNCTIONS OF
STATISTICAL ANALYSIS
• STATISTICAL ANALYSIS: The refinement
and manipulation of data that prepares them
for the application of logical inferences.
• Statistical analytical methods may be used in
valid ways or in specious ways. This depends
both on the honesty of the researcher in
selecting the appropriate formulas and data
inputs, and on his or her understanding of the
formulas and their outputs.

6. 6
NATURE AND FUNCTIONS OF
STATISTICAL ANALYSIS – Contd.
• For each analytical method, there is an
appropriate sequence that can be used.
• However, there are three chief phases
for analysis:
–Bringing the raw data into order (arrays,
tabulations, establishing categories,
percentages)

7. 7
NATURE AND FUNCTIONS OF
STATISTICAL ANALYSIS – Contd.
–Summarising the data: measures of central
tendency and dispersion, and graphical
presentation
–Applying analytical methods to manipulate
the data so that their interrelationships and
quantitative meaning become evident. For
this purpose an appropriate analytical
method is to be selected: Selection criteria

8. 8
INTERRELATIONSHIP BETWEEN
ANALYSIS AND INTERPRETATION
(a) Consider the following exchange regarding
survey data:
• RESEARCHER: Look at the answers to a
question, “If you were buying an electric
range or a gas range completely equipped
with all modern features, what would it price
be?” Average price given for electric range
was Rs. 11,900 and for gas range was Rs.
10,250. I think, it is advantageous for the gas
range.

9. 9
INTERRELATIONSHIP BETWEEN
ANALYSIS AND INTERPRETATION
• MARKETING MANAGER: I wouldn’t say
that at all. It seems to me what that shows is,
that most women just cannot conceive of a
gas range that has all the features of a modern
range. So, that is a mark against gas.
• As per the researcher, the company would
have gone for gas ranges. In light of the data
collected, a proper analysis has been made by
the researcher. However, the interpretation
made was faulty because the data were not
properly related to other information that the
Marketing Manager had injected.

10. 10
INTERRELATIONSHIP BETWEEN
ANALYSIS AND INTERPRETATION
(b) Suppose that a detergent manufacturer is
trying to decide which of three advertisements
would be the most effective in increasing sales
of their detergent. They test the three ads by
running each at different times in newspapers
in six different cities. Sales are
Advertise 1 2 3
Sales of boxes 2,396 3,654 2,576
This indicates that the ad 2 is the most effective.

11. 11
INTERRELATIONSHIP BETWEEN
ANALYSIS AND INTERPRETATION
• Looking to the big difference, the researcher
felt that there may be another variable. Hence,
following table was prepared:
Advt. A B C D E F TOTAL
1 379 400 420 380 421 396 2,396
2 401 384 1527 424 447 471 3,654
3 429 351 451 425 487 433 2,576

12. 12
INTERRELATIONSHIP BETWEEN
ANALYSIS AND INTERPRETATION
• There was an unusual demand during
advertisement 2 in city C, otherwise three
advertisements did not differ significantly
in any city.
• If the researcher had used the combined
data, it would have been an improper
analysis, but correct interpretation.

13. 13
INTERPRETIVE PROCESS
• Our perceptions can be distorted and
limited very easily, and our thinking
processes can take wrong turns too easily.
• There is no truth in the adage that
“figures speak for themselves”.
• When people have the figures to interpret,
they state what the figures mean, and
dangerous errors are often committed.

14. 14
INTERPRETIVE PROCESS
• Firm discipline over one’s mental processes
and the ability to work as dispassionately as
possible are necessary.
• For this purpose, every researcher will have
to follow certain maxims. They can be:
1. Produce honest and sober interpretations.
2. Keep objectives and simple principles in
the forefront.

15. 15
INTERPRETIVE PROCESS
3. Beware of the limitations of small samples.
4. Give fair weight to all evidence.
5. Give due attention to infrequent significant
answers.
6. Recognise averages as mere tendencies.
7. Distinguish between opinion and fact.
8. Look for causes and do not confuse them
with effects.

16. 16
BRINGING THE DATA INTO ORDER
• Simplest way in which data can be
brought into order is an array. This is a
simple tabulation.
- Minimum and maximum can be found.
- Range can be found.
- Quartiles can be found.
- Mode can be found.
• When there are only a few observations,
setting up an array may not be too
tedious.

17. 17
BRINGING THE DATA INTO ORDER
• In spite of the advantages of data array, this
would be inefficient with a sizable array of
data such as is usually obtained in a marketing
study. For such data, suitable classifications
are to be established. Then, we can place
individual observations in those categories.
This is called a simple tabulation. It is also
referred to as a ‘one-way’ or a ‘marginal’
tabulation.

18. 18
BRINGING THE DATA INTO ORDER
• Many research questions may be answered by
simple tabulation of data. However, simple
tabulation merely shows a distribution of one
variable at a time, and may not yield the full
value of data. Most data can be further
organised to yield additional information.
Cross-tabulation is an extension of one
dimensional form in which the researcher can
investigate the relationship between two or
more variables by simultaneously counting the
number of responses that fall in each of the
classifications.

19. 19
Types of Statistical Analyses Used in
Marketing Research
Copyright © 2010 PearsonCopyright © 2010 Pearson
Education, Inc. publishing asEducation, Inc. publishing as
Prentice HallPrentice Hall

20. 20
Types of Statistical Analyses Used
in Marketing Research
• Five Types of Statistical Analysis:
1. Descriptive analysis: used to describe
the data set
2. Inferential analysis: used to generate
conclusions about the population’s
characteristics based on the sample
data

21. 21
Types of Statistical Analyses Used
in Marketing Research
3. Differences analysis: used to compare
the mean of the responses of one group
to that of another group
4. Associative analysis: determines the
strength and direction of relationships
between two or more variables
5. Predictive analysis: allows one to make
forecasts for future events

22. 22
A Classification of Univariate Techniques
Independent Related
Independent Related
* Two- Group test
* Z test
* One-Way
ANOVA
* Paired
t test * Chi-Square
* Mann-Whitney
* Median
* K-S
* K-W ANOVA
* Sign
* Wilcoxon
* McNemar
* Chi-Square
Metric Data Non-numeric Data
Univariate Techniques
One Sample Two or More
Samples
One Sample Two or More
Samples
* t test
* Z test
* Frequency
* Chi-Square
* K-S
* Runs
* Binomial

23. 23
A Classification of Multivariate Techniques
More Than One
Dependent
Variable
* Multivariate
Analysis of
Variance and
Covariance
* Canonical
Correlation
* Multiple
Discriminant
Analysis
* Cross-
Tabulation
* Analysis of
Variance and
Covariance
* Multiple
Regression
* Conjoint
Analysis
* Factor
Analysis
One Dependent
Variable
Variable
Interdependence
Interobject
Similarity
* Cluster Analysis
* Multidimensional
Scaling
Dependence
Technique
Interdependence
Technique
Multivariate Techniques

24. 24
WHEN TO USE A PARTICULAR
STATISTIC
Copyright © 2010 Pearson Education, Inc.Copyright © 2010 Pearson Education, Inc.
publishing as Prentice Hallpublishing as Prentice Hall

25. 25
Statistics Associated with Cross-Tabulation
Phi Coefficient
• The phi coefficient (φ) is used as a measure of the
strength of association in the special case of a table with
two rows and two columns (a 2 x 2 table).
• The phi coefficient is proportional to the square root of
the chi-square statistic:
• It takes the value of 0 when there is no association,
which would be indicated by a chi-square value of 0 as
well. When the variables are perfectly associated, phi
assumes the value of 1 and all the observations fall just
on the main or minor diagonal.
φ =
χ2
n

26. 26
Statistics Associated with Cross-Tabulation
Contingency Coefficient
• While the phi coefficient is specific to a 2 x 2 table, the
contingency coefficient (C) can be used to assess the
strength of association in a table of any size.
• The contingency coefficient varies between 0 and 1.
• The maximum value of the contingency coefficient
depends on the size of the table (number of rows and
number of columns). For this reason, it should be used
only to compare tables of the same size.
C =
χ2
χ2 + n

27. 27
Statistics Associated with Cross-Tabulation
Cramer’s V
• Cramer's V is a modified version of the phi
correlation coefficient, φ, and is used in tables
larger than 2 x 2.
or
V =
φ
2
min (r-1), (c-1)
V =
χ2/n
min (r-1), (c-1)