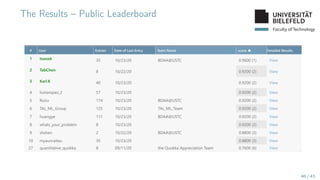
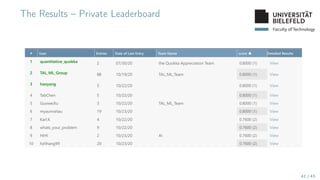
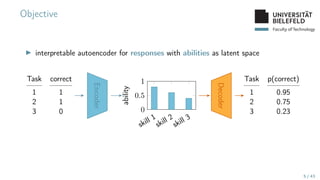
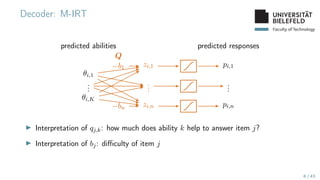
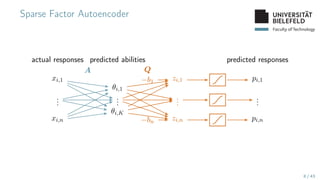
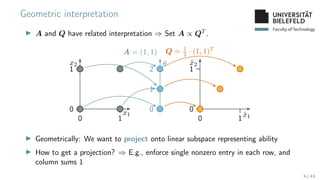
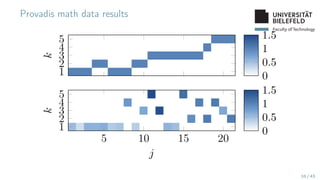
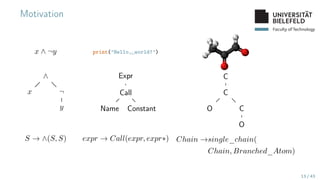
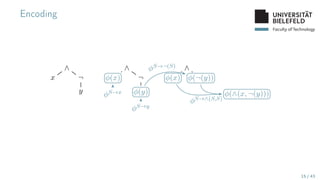
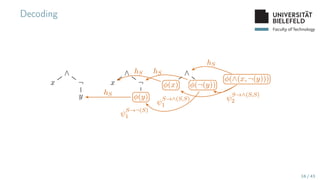
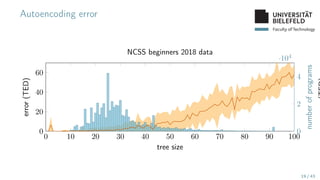
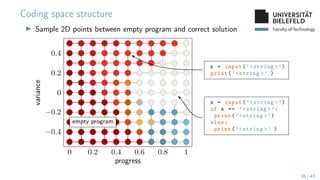
The document presents various topics in data mining, including autoencoders, tree grammars, and prediction methods. It discusses the development of interpretable models and their applications in tasks such as predicting student programming responses. Additionally, the document shares insights into competitions and runtime optimization concerns regarding algorithm performance.

1. Faculty of Technology
Introduction to Data Mining
11 - Winter Lecture
Benjamin Paaßen
WS 2023/2024, Bielefeld University
1 / 43

2. Faculty of Technology
Interdisciplinary College
▶ Spring School March 1st to March 8th
▶ AI, Neurobiology, Cognitive Science, . . .
▶ Especially helpful for research-oriented students
▶ Program: Link
▶ Registration (and stipend application): Link
2 / 43

3. Faculty of Technology
Sparse Factor Autoencoder
3 / 43

4. Faculty of Technology
Motivation
Assignment sheet:
1. Write a function which adds two numbers.
2. Write a function which sorts a list of numbers.
3. Write an implementation of the A∗ algorithm.
▶ How much ability do the answers reveal?
▶ Which abilities would explain the answers?
4 / 43

5. Faculty of Technology
Objective
▶ interpretable autoencoder for responses with abilities as latent space
Task correct
1 1
2 1
3 0
Encoder
skill 1
skill 2
skill 3
0
0.5
1
ability
Decoder
Task p(correct)
1 0.95
2 0.75
3 0.23
5 / 43

6. Faculty of Technology
Decoder: M-IRT
predicted abilities
θi,1
.
.
.
θi,K
predicted responses
pi,1
.
.
.
pi,n
Q
−b1
−bn
zi,1
.
.
.
zi,n
▶ Interpretation of qj,k: how much does ability k help to answer item j?
▶ Interpretation of bj: difficulty of item j
6 / 43

7. Faculty of Technology
Encoder
actual responses
xi,1
.
.
.
xi,n
predicted abilities
θi,1
.
.
.
θi,K
A
▶ Interpretation of ak,j: how much ability k does a correct answer on item j reveal?
▶ Alternatively: how much points for a correct answer to item j, according to kth
scoring scheme
7 / 43

8. Faculty of Technology
Sparse Factor Autoencoder
actual responses
xi,1
.
.
.
xi,n
predicted responses
pi,1
.
.
.
pi,n
predicted abilities
θi,1
.
.
.
θi,K
A Q
−b1
−bn
zi,1
.
.
.
zi,n
8 / 43

9. Faculty of Technology
Geometric interpretation
▶ A and Q have related interpretation ⇒ Set A ∝ QT .
x1
x2
0 1
0
1
θ
0
1
2
A = (1, 1)
x̂1
x̂2
0 1
0
1
Q = 1
2 · (1, 1)T
▶ Geometrically: We want to project onto linear subspace representing ability
▶ How to get a projection? ⇒ E.g., enforce single nonzero entry in each row, and
column sums 1
9 / 43

10. Faculty of Technology
Provadis math data results
1
2
3
4
5
k
0
0.5
1
1.5
5 10 15 20
1
2
3
4
5
j
k
0
0.5
1
1.5
10 / 43

11. Faculty of Technology
Summary
▶ Highly interpretable model with single-layer encoder and decoder
▶ Resulting model is similar to factor analysis, but not exactly the same (no strict
projection, only non-negative coefficients)
11 / 43

12. Faculty of Technology
Recursive Tree Grammar Autoencoder
12 / 43

13. Faculty of Technology
Motivation
x ∧ ¬y
∧
x ¬
y
S → ∧(S, S)
print(’Hello,␣world!’)
Expr
Call
Name Constant
expr → Call(expr, expr∗)
C
C
C
O
O
Chain →single_chain(
Chain, Branched_Atom)
13 / 43

14. Faculty of Technology
Example Regular Tree Grammar
▶ We wish to express trees of Boolean formulae over variables x and y
▶ Only one nonterminal S (which is also the starting symbol)
▶ Rules: S → ∧(S, S), S → ∨(S, S), S → x(), S → y()
▶ Side node: Regular tree grammar are quite similar to context-free grammars – but
much easier to parse
14 / 43

15. Faculty of Technology
Encoding
∧
x ¬
y
∧
ϕ(x) ¬
ϕ(y)
ϕS→x
ϕS→y
∧
ϕ(x) ϕ(¬(y))
ϕS→¬(S)
ϕ(∧(x, ¬(y)))
ϕS→∧(S,S)
15 / 43

16. Faculty of Technology
Decoding
ϕ(∧(x, ¬(y)))
∧
ϕ(x) ϕ(¬(y))
hS
ψ
S→∧(S,S)
1
ψ
S→∧(S,S)
2
∧
x ¬
ϕ(y)
hS hS
ψ
S→¬(S)
1
∧
x ¬
y hS
16 / 43

17. Faculty of Technology
Theory
1. If the right-hand-side in a regular tree grammar is unique (deterministic), then the
generating rule sequence for each tree is unique
2. Any regular tree grammar can be re-written as deterministic
3. Iff a tree with n nodes is valid, our encoding finds the unique rule sequence for it
in O(n)
4. If our decoding terminates, the resulting tree is valid
17 / 43

18. Faculty of Technology
Training the autoencoder
▶ 448, 992 Python programs from the beginners challenge of the 2018 National
Computer Science School
▶ encoding dimension 256, crossentropy loss, learning rate 10−3, ADAM optimizer
▶ ca. 1 week of training time, 130k batches of 32 programs each
▶ Result: ast2vec, a pre-trained neural network
18 / 43

19. Faculty of Technology
Autoencoding error
0
2
4
·104
number
of
programs
0 10 20 30 40 50 60 70 80 90 100
0
20
40
60
tree size
error
(TED)
NCSS beginners 2018 data
19 / 43

20. Faculty of Technology
Coding space structure
▶ Sample 2D points between empty program and correct solution
0 0.2 0.4 0.6 0.8 1
−0.4
−0.2
0
0.2
0.4
progress
variance
empty program
x = input(’<string >’)
print(’<string >’ )
x = input(’<string >’)
if x == ’<string >’:
print(’<string >’)
else:
print(’<string >’ )
20 / 43

21. Faculty of Technology
Progress-Variance plot
▶ x-axis: direction from empty solution to goal; y-axis: orthogonal direction with
maximum variance
0 0.2 0.4 0.6 0.8 1
0
0.5
1
progress
variance
print(’<string >’ )
input(’<string >’)
print(’<string >’ )
x = input(’<string >’)
if x == ’<string >’:
print(’<string >’)
else:
print(’<string >’ )
21 / 43

22. Faculty of Technology
Clustering
0 0.2 0.4 0.6 0.8 1
0
0.5
1
progress
variance
x = input(’<string >’)
if x == ’<string >’:
print(f(’<string >’ + x
))
x = input(’<string >’)
if x == ’<string >’:
print(’<string >’ )
x = input(’<string >’)
print(’<string >’ )
input(’<string >’)
print(’<string >’ )
22 / 43

23. Faculty of Technology
Prediction
▶ Predict a student’s next program as f(⃗
x) = ⃗
x + W · (⃗
b − ⃗
x)
▶ Learn W via linear regression; set ⃗
b to closest correct solution
⇒ Provably converges to ⃗
b (for strong enough regularization)
0 0.2 0.4 0.6 0.8 1
−0.5
0
0.5
progress
variance
x = input(’<string >’ )
x = input(’<string >’)
print(’<string >’ )
x = input(’<string >’)
if x == ’<string >’:
print(’<string >’)
else:
print(’<string >’ )
23 / 43

24. Faculty of Technology
Summary
▶ (Variational) Autoencoders are a very general concept that is applicable to a
plethora of data types (vectors, images, trees, . . .)
▶ Training is usually performed via backpropagation (deep learning)
⇒ Easiest implementation: pytorch
▶ Caveat: State-of-the-art results are usually achieved with different architectures
(transformers, diffusion models, . . .)
24 / 43

25. Faculty of Technology
Echo State Nets & Legendre Delay Nets
25 / 43

26. Faculty of Technology
Motivation
▶ What if we don’t train f but only the output layer g?
⇒ Pre-compute states h1, . . . , hT , perform linear regression to find optimal weights
for g, such that g(ht) ≈ xt+1
▶ But: How to set f, then?
26 / 43

27. Faculty of Technology
Echo State Networks (Jaeger and Haas 2004)
▶ Formalization: ht = f(xt) = tanh
U · xt + W · ht−1
with fixed U and W
▶ f must ensure echo state property, i.e. the initial state h0 must wash out over
time
▶ Standard ESNs: Random initialization and down-scaling of W
▶ More reliable: deterministic construction (Rodan and Tiňo 2012, “cycle reservoir
with jumps”)
27 / 43

28. Faculty of Technology
ESN/CRJ Visualization
xt ht x̂t+1
−u
−u
−u
−u
+u
+u
U
w
w
w
w
w
w
W
wjump
wjump
w
jump
V
▶ Choose signs of U via digits of π (-1 for 0-4, +1 for 5-9)
▶ Hyper-parameters: input weight u, cycle weight w, jump weight wjump, jump
length l
28 / 43

29. Faculty of Technology
Legendre delay network
(Voelker, Kajić, and Eliasmith 2019; Stöckel 2022)
▶ Idea: Is there an optimal way to construct U and W ?
▶ Assume one-dimensional, continuous signal xt and no nonlinearity
▶ Using only m neurons, we want to have a delay operator by θ time steps: yt
should be xt−θ
▶ By Laplace transform and Padé approximation, you end up with:
ui =
1
θ
· (−1)i
wi,j =
(
−1
θ · (2i − 1) if i ≤ j
−1
θ · (2i − 1) · (−1)i−j if i j
⇒ State ht encodes the signal in the past θ time steps as well as possible
▶ careful: Only for continuous signals; discrete approximation requires small time
steps (Euler method) or extra math
29 / 43

30. Faculty of Technology
LDN: Visualization
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 1
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 2
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 3
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 4
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 5
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 6
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 10
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 20
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 40
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
1 2 3
Time t
Input u(t)
1 2 3
Time t
q = 50
System state m(t)
1 2 3
Time t
Output Cm(t) ≈ u(t − θ)
30 / 43

31. Faculty of Technology
Summary
▶ Highly efficient, easy-to-train variants of recurrent networks
▶ Assumption: Encoding the past θ time steps is what we need to predict the target
(in this case: the next time step)
▶ Optimal encoding in continuous, linear case: Legendre delay net (and other “state
space” nets)
Modified Fourier Basis
31 / 43

32. Faculty of Technology
The Five Words Problem
32 / 43

33. Faculty of Technology
Wordle
▶ Question: Which five words of five letters each permit you to cover 25 different
letters of the alphabet?
▶ Source: Hill Parker: A problem squared episode 38
33 / 43

34. Faculty of Technology
Pseudocode
Assume X is the set of 5-letter words of the English language
for u ∈ X do
for word v ∈ X with v u and v ∩ u = ∅ do
for word w ∈ X with w v and w ∩ (u ∪ v) = ∅ do
for word x ∈ X with x w and x ∩ (u ∪ v ∪ w) = ∅ do
for word y ∈ X with y x and y ∩ (u ∪ v ∪ w ∪ x) = ∅ do
Print the solution (u, v, w, x, y).
end for
end for
end for
end for
end for
34 / 43

35. Faculty of Technology
Solution
▶ 831 unique solutions (excluding permutations)
▶ often contains “unusual” words, e.g.
curby fldxt ginks vejoz whamp
flong japyx twick verbs zhmud
glack hdqrs jowpy muntz vibex
35 / 43

36. Faculty of Technology
Runtime
▶ Main challenge: Runtime! Several 10k words with 5 letters in the English
language; O(n5) algorithm
▶ Matt Parker’s original solution: over one month of runtime
▶ My solution: About 15 min
▶ Matt Parker released a YouTube video on it – and actual programming experts got
wind of it
36 / 43

37. Faculty of Technology
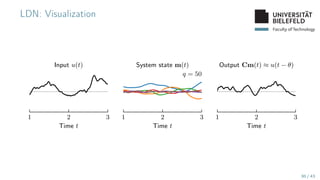
Runtime (continued)
0 5 10 15 20 25 30 35 40 45 50 55
10−4
10−2
100
102
104
106
standupmaths
bpaassen
neilcoffey
IlyaNikolaevsky
gweijers
KristinPaget
orlp
oisyn
miniBill
oisyn stew675
stew675 GuiltyBystander
video release
days since podcast
runtime
[s]
Python
Java
C++
C
Rust
Julia
Go
▶ Full leaderboard: Link
▶ Second YouTube video: Link
37 / 43

38. Faculty of Technology
How we won a NeurIPS data mining competition
38 / 43

39. Faculty of Technology
Task description
39 / 43

40. Faculty of Technology
The Results – Public Leaderboard
40 / 43

41. Faculty of Technology
The Results – Private Leaderboard
41 / 43

42. Faculty of Technology
The Winners
42 / 43

43. Faculty of Technology
The methods used
43 / 43

44. Faculty of Technology
Literature I
Jaeger, Herbert and Harald Haas (2004). “Harnessing Nonlinearity: Predicting Chaotic
Systems and Saving Energy in Wireless Communication”. In: Science 304.5667,
pp. 78–80. DOI: 10.1126/science.1091277.
Paaßen, Benjamin, Malwina Dywel, et al. (July 24, 2022). “Sparse Factor Autoencoders
for Item Response Theory”. In: Proceedings of the 15th International
Conference on Educational Data Mining (EDM 2022) (Durham, UK). Ed. by
Alexandra I. Cristea et al., pp. 17–26. DOI: 10.5281/zenodo.6853067.
Paaßen, Benjamin, Irena Koprinska, and Kalina Yacef (2022). “Recursive Tree Grammar
Autoencoders”. In: Machine Learning 111. Special Issue of the ECML PKDD 2022
Journal Track, pp. 3393–3423. DOI: 10.1007/s10994-022-06223-7. URL:
https://arxiv.org/abs/2012.02097.
44 / 43

45. Faculty of Technology
Literature II
Paaßen, Benjamin, Jessica McBroom, et al. (2021). “Mapping Python Programs to
Vectors using Recursive Neural Encodings”. In: Journal of Educational
Datamining 13.3, pp. 1–35. DOI: 10.5281/zenodo.5634224. URL: https:
//jedm.educationaldatamining.org/index.php/JEDM/article/view/499.
Rodan, Ali and Peter Tiňo (2012). “Simple Deterministically Constructed Cycle
Reservoirs with Regular Jumps”. In: Neural Computation 24.7, pp. 1822–1852.
DOI: 10.1162/NECO_a_00297.
Stöckel, Andreas (2022). “Harnessing Neural Dynamics as a Computational Resource”.
PhD Thesis. University of Waterloo. URL:
https://uwspace.uwaterloo.ca/handle/10012/17850.
Voelker, Aaron, Ivana Kajić, and Chris Eliasmith (2019). “Legendre Memory Units:
Continuous-Time Representation in Recurrent Neural Networks”. In: Advances in
Neural Information Processing Systems. Ed. by H. Wallach et al. Vol. 32.
Curran Associates, Inc. URL: https://proceedings.neurips.cc/paper_files/
paper/2019/file/952285b9b7e7a1be5aa7849f32ffff05-Paper.pdf.
45 / 43