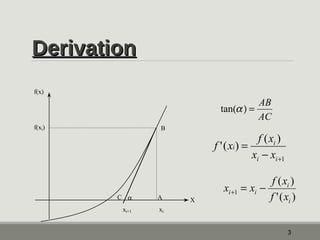
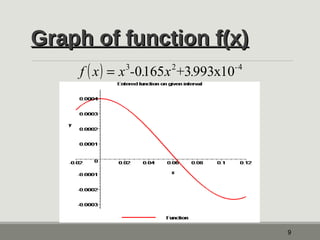
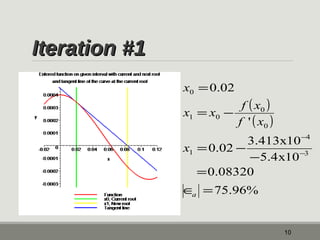
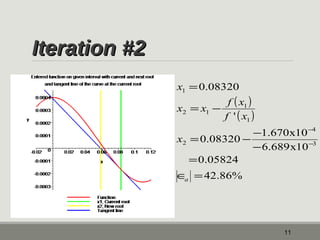
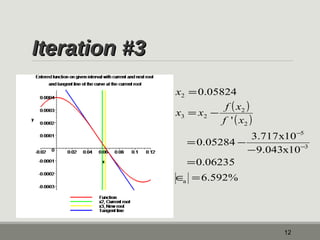
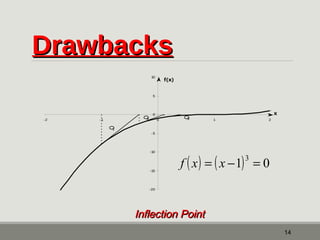
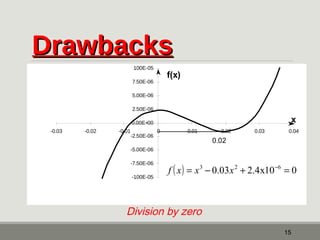
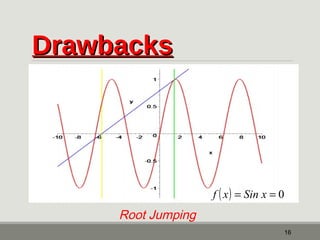
The document outlines the Newton-Raphson method for solving non-linear equations, detailing the steps for iteration and root estimation. It includes an example demonstrating three iterations on a specific function to find its root. Additionally, it discusses the advantages and drawbacks of the method, such as its rapid convergence and potential issues like root jumping.

1. RRoooottss ooff aa NNoonnlliinneeaarr
EEqquuaattiioonn
NNeewwttoonn--RRaapphhssoonn
MMeetthhoodd
1

2. NNeewwttoonn--RRaapphhssoonn MMeetthhoodd
x = x - f(x )
i
f (x )
2
i
i+1 i ¢
f(x)
f(xi)
f(xi-1)
q
[ ( ) ] i i x f x ,
xi+2 xi+1 xi X

3. DDeerriivvaattiioonn
tan(a ) = AB
AC
f x f x
i i x x
+ -
1
'( ) ( )
( )
i
=
i i
i i f x
3
f(x)
f(xi)
xi+1 xi
X
B
1
C a A '( )
i
x = x - f x +

4. AAllggoorriitthhmm ffoorr NNeewwttoonn--
RRaapphhssoonn MMeetthhoodd
4

5. SStteepp 11
Evaluate f¢(x) symbolically
5

6. SStteepp 22
6
Calculate the next estimate of the root
x = x - f(x )
i
f'(x )
i
i+1 i
Find the absolute relative approximate error
x 100
= x - x
i i
1
1
x
i
a
+
Î +

7. SStteepp 33
Find if the absolute relative approximate error is greater
than the pre-specified relative error tolerance.
If so, go back to step 2, else stop the algorithm.
Also check if the number of iterations has exceeded the
maximum number of iterations.
7

8. EExxaammppllee
Solve the given equation using Newton’s method using 3 iterations:
8
f ( x) = x3-0.165x2+3.993x10-4

9. GGrraapphh ooff ffuunnccttiioonn ff((xx))
9
f ( x) = x3-0.165x2+3.993x10-4

10. IItteerraattiioonn ##11
x x f x
0
=
= -
0.02 3.413x10
10
( )
( )
0.08320
75.96%
5.4x10
'
0.02
-
4
3
0
1
0
1 0
=
Î =
-
= -
-
a
x
f x
x

11. IItteerraattiioonn ##22
0.08320
x x f x
1
=
= - -
0.08320 1.670x10
11
( )
( )
0.05824
42.86%
-
6.689x10
'
4
3
1
2
1
2 1
=
Î =
-
= -
-
a
x
f x
x

12. IItteerraattiioonn ##33
0.05824
2
=
x = x -
f x
0.05284 3.717x10
12
( )
( )
0.06235
6.592%
-
9.043x10
'
2
a
3
5
2
3 2
=
Î =
-
= -
-
f x
x

13. AAddvvaannttaaggeess
CCoonnvveerrggeess ffaasstt,, iiff iitt ccoonnvveerrggeess
RReeqquuiirreess oonnllyy oonnee gguueessss
13

14. DDrraawwbbaacckkss
14
10
5
0
f(x)
-2 -1 0 1 2
-5
-10
-15
-20
1
2 3
x
f ( x) = ( x -1)3 = 0
IInnfflleeccttiioonn PPooiinntt

15. DDrraawwbbaacckkss
-0.03 -0.02 -0.01 0 0.01 0.02 0.03 0.04
f ( x) = x3 - 0.03x2 + 2.4x10-6 = 0
15
1.00E-05
7.50E-06
5.00E-06
2.50E-06
0.00E+00
-2.50E-06
-5.00E-06
-7.50E-06
-1.00E-05
x
f(x)
0.02
Division by zero

16. DDrraawwbbaacckkss
16
Root Jumping
f ( x) = Sin x = 0

17. 17