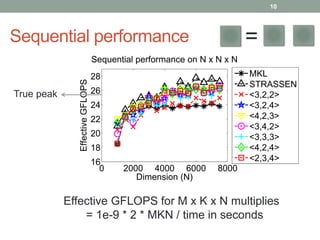
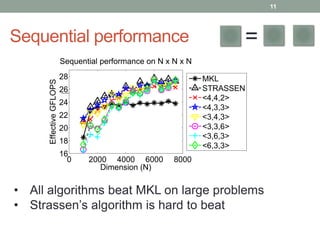
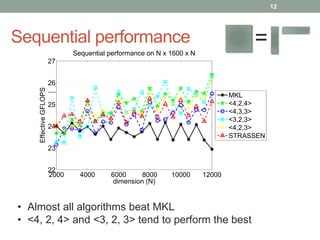
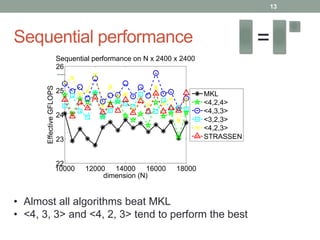
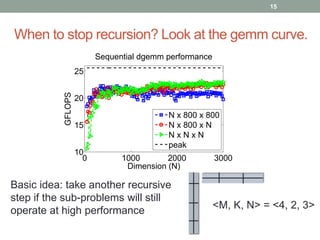
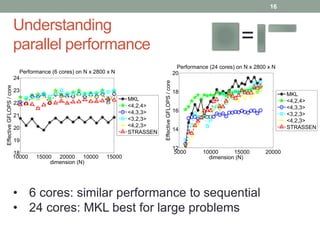
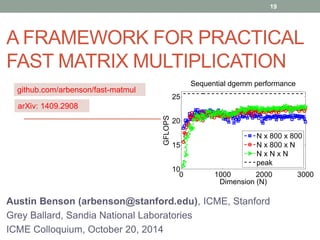
This document presents a framework for practical fast matrix multiplication algorithms that can achieve higher performance than Intel's MKL library. It describes several algorithms discovered recently, including Strassen's algorithm, that partition matrices and use fewer multiplication operations through linear combinations. Code generation is used to rapidly prototype the algorithms. Evaluation shows the algorithms generally outperform MKL, with Strassen's best for square matrices and others like <4,2,4> better for rectangular matrices. Parallel performance is limited by memory bandwidth.
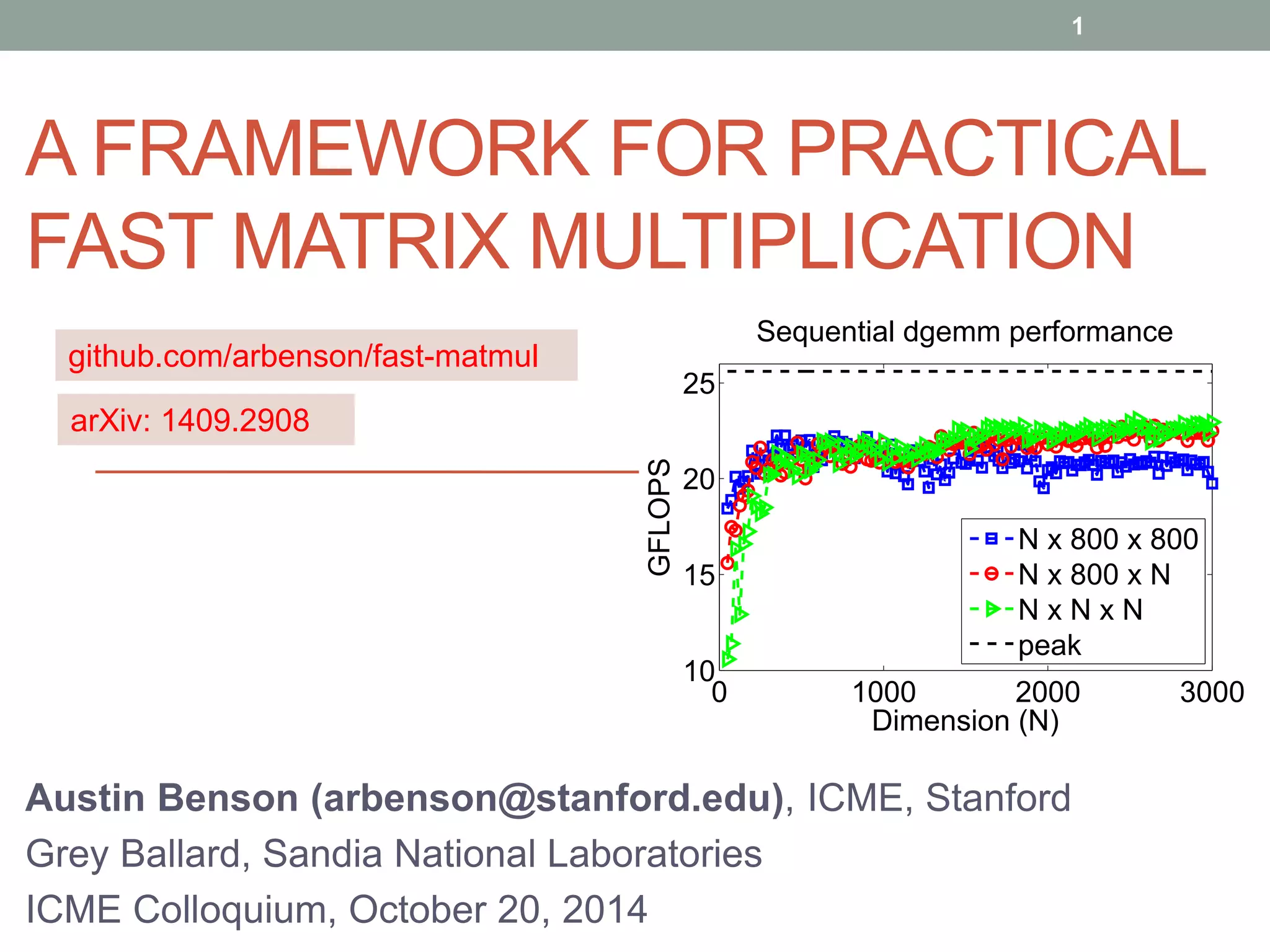
![Fast matrix multiplication:
bridging theory and practice
2
• There are a number of Strassen-like algorithms for matrix
multiplication that have only been “discovered” recently.
[Smirnov13], [Benson&Ballard14]
• We show that they can achieve higher performance with respect
to Intel Math Kernel Library (MKL).
• We use code generation for extensive prototyping.
2 2.81 3
[Strassen79]
2.37
[Williams12]
xxxxx xxx x](https://image.slidesharecdn.com/icmecolloqfastmatmul-141021214804-conversion-gate02/85/A-framework-for-practical-fast-matrix-multiplication-2-320.jpg)




![Discovering fast algorithms is a
numerical challenge
7
• Low-rank tensor decompositions lead to fast algorithms
• Tensors are small, but we need exact decompositions
NP-hard
• Use alternating least squares with regularization and
rounding tricks [Smirnov13], [Benson&Ballard14]
• We have around 10 fast algorithms for <M, K, N>
decompositions. Also have permutations like <K, M, N>.](https://image.slidesharecdn.com/icmecolloqfastmatmul-141021214804-conversion-gate02/85/A-framework-for-practical-fast-matrix-multiplication-7-320.jpg)
![8
[Strassen69]
[Smirnov13]](https://image.slidesharecdn.com/icmecolloqfastmatmul-141021214804-conversion-gate02/85/A-framework-for-practical-fast-matrix-multiplication-8-320.jpg)