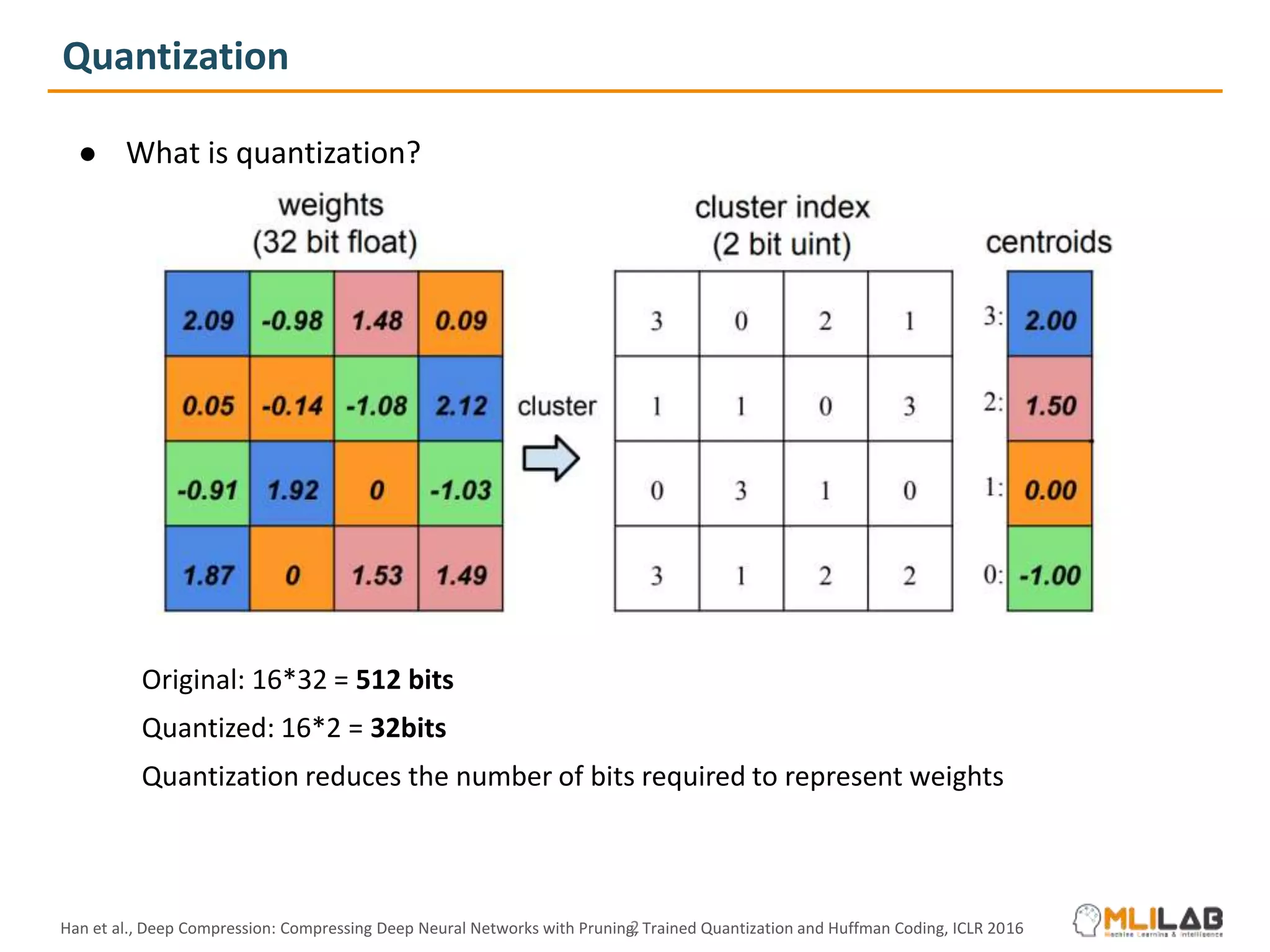
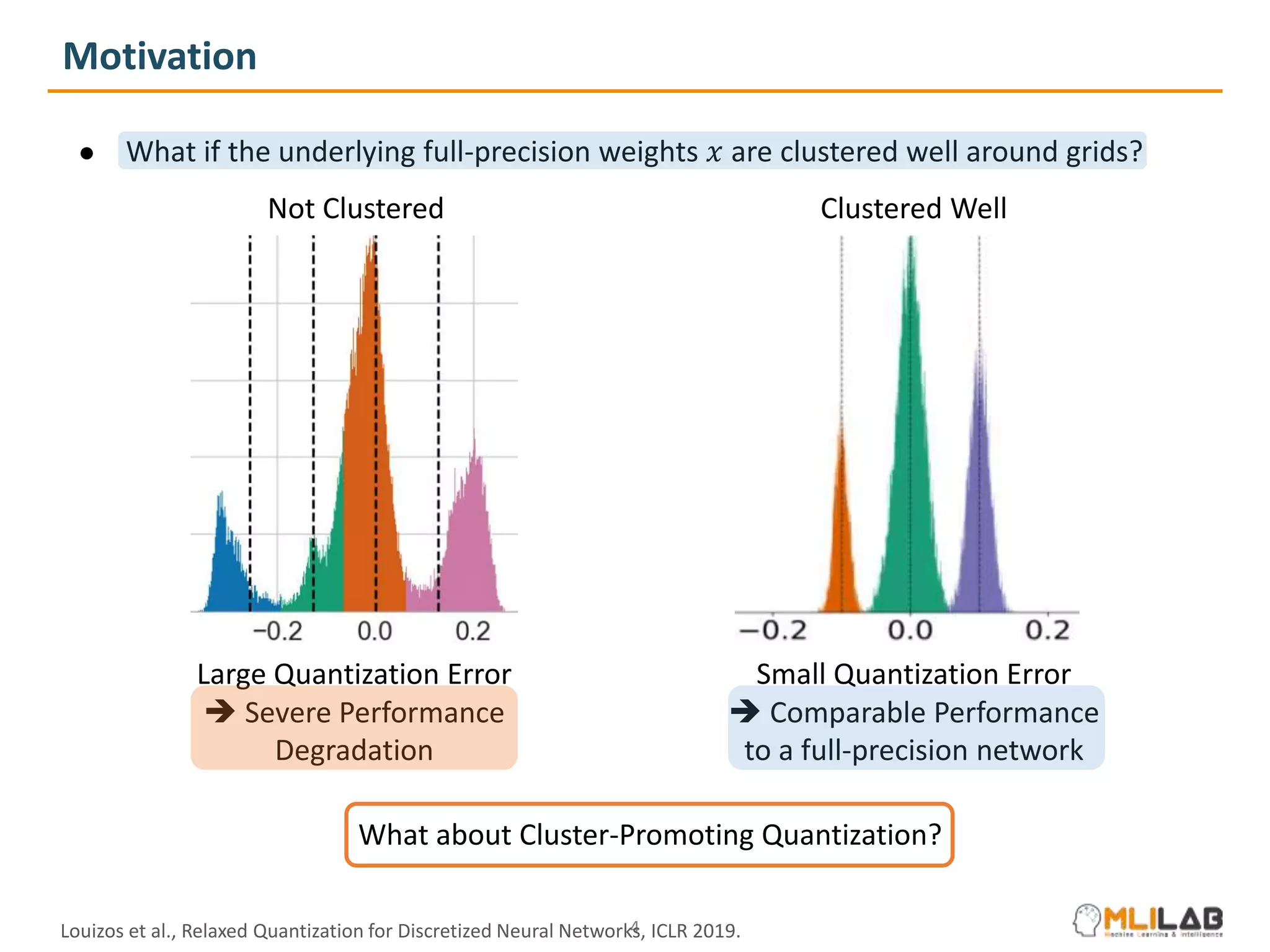
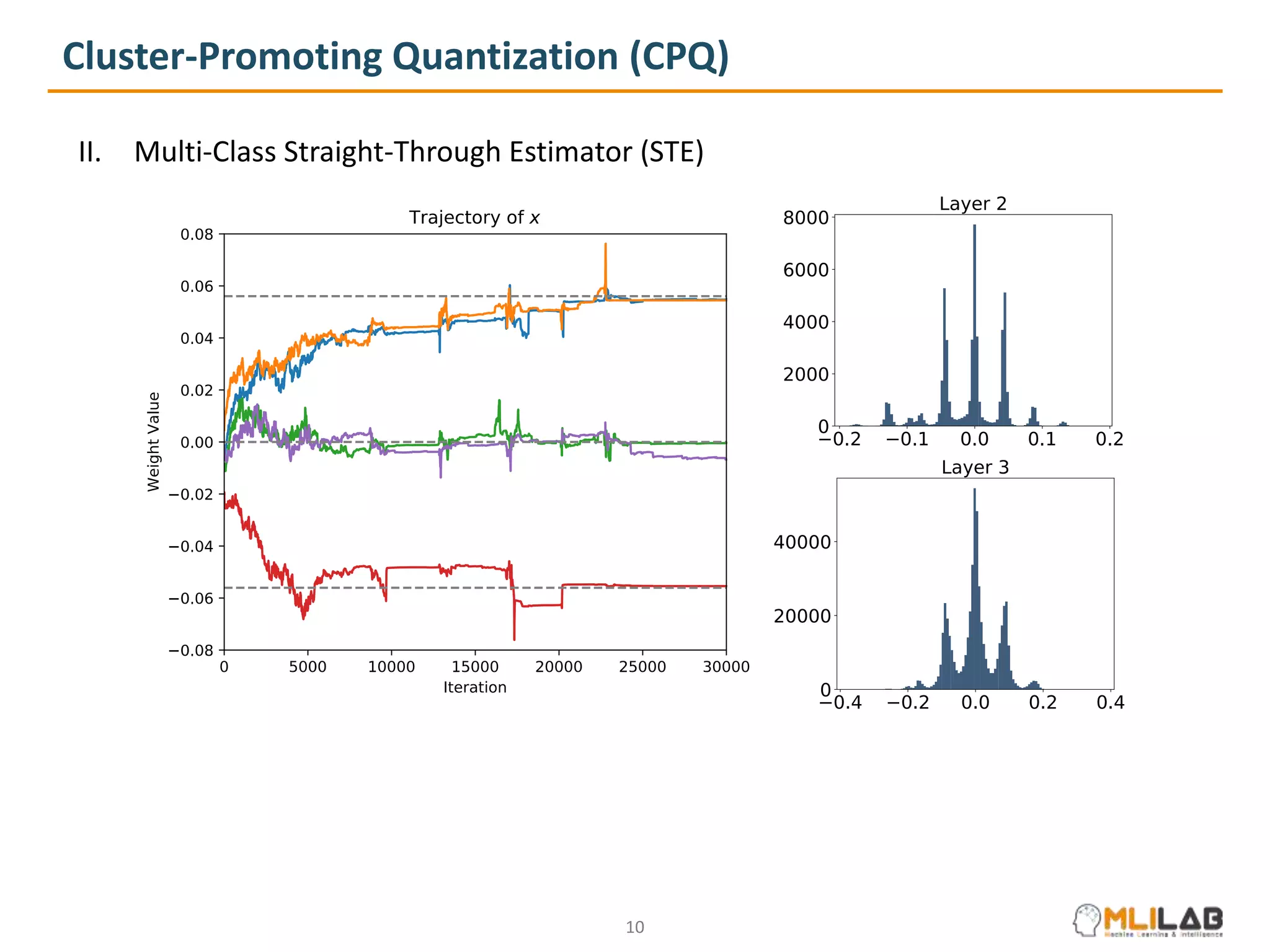
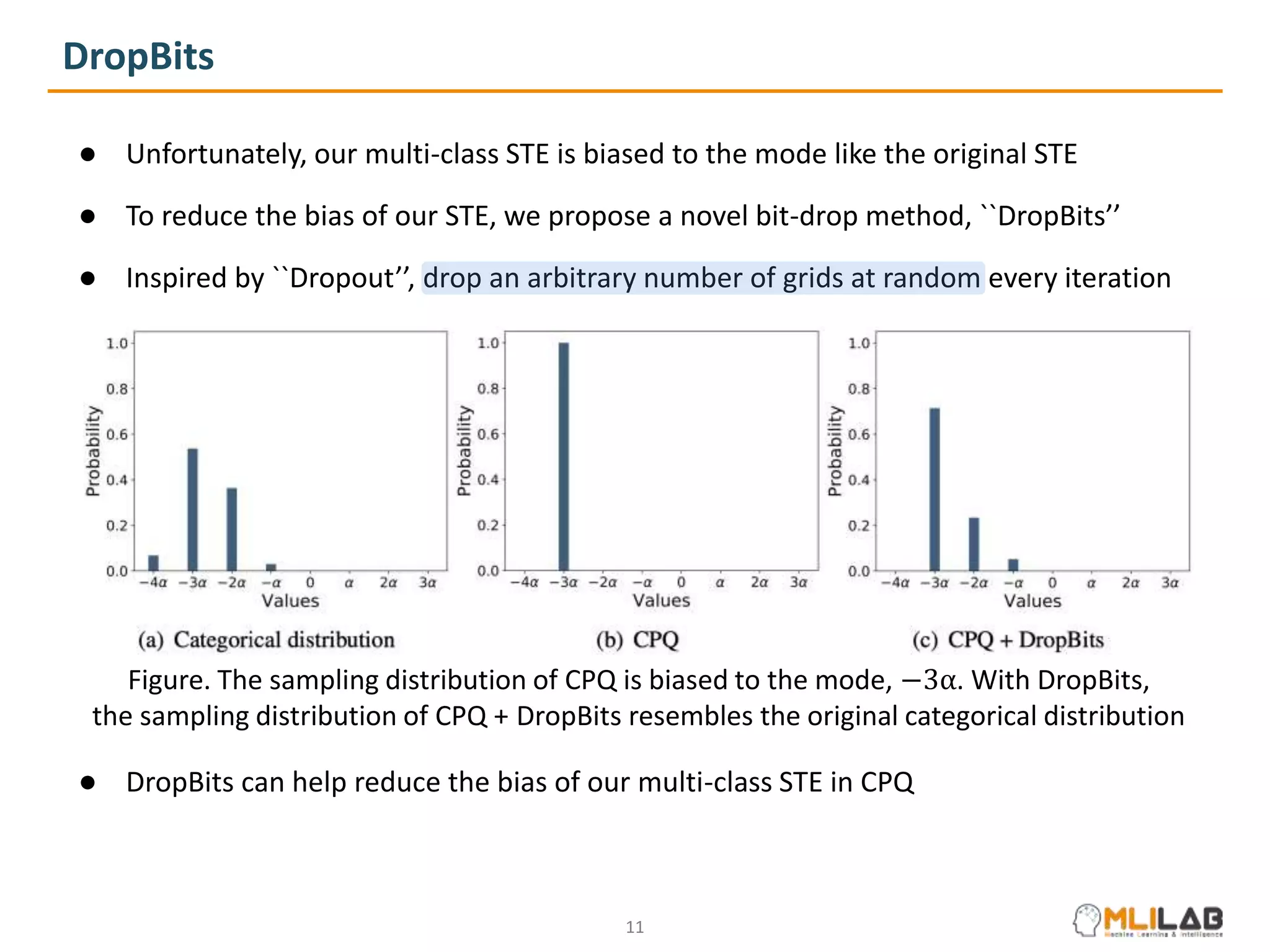
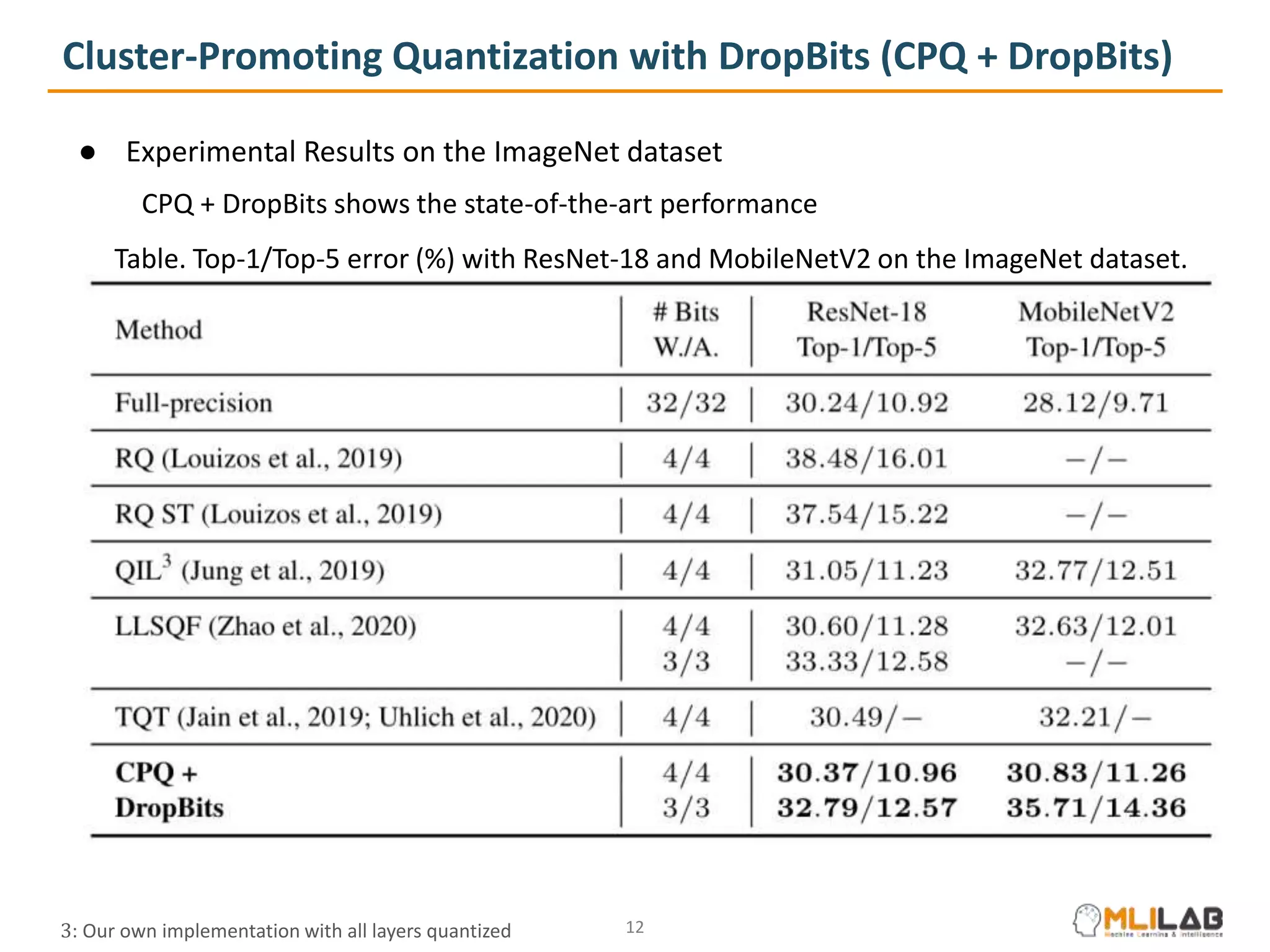
The document presents a novel method called cluster-promoting quantization (CPQ) aimed at reducing quantization loss in neural network models by clustering full-precision weights around optimal quantization grids. It introduces a bit-drop technique, 'dropbits', to mitigate biases in the multi-class straight-through estimator (STE) used in CPQ. Experimental results demonstrate that the combination of CPQ and dropbits achieves state-of-the-art performance on the ImageNet dataset for models like ResNet-18 and MobileNetV2.

1. Cluster-Promoting Quantization with Bit-Drop
for Minimizing Network Quantization Loss
Jung Hyun Lee*, Jihun Yun*, Sung Ju Hwang, and Eunho Yang
Korea Advanced Institute of Science and Technology

2. Quantization
● What is quantization?
Original: 16*32 = 512 bits
Quantized: 16*2 = 32bits
Quantization reduces the number of bits required to represent weights
2
Han et al., Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding, ICLR 2016

3. Quantization
● Why is quantization required?
Quantization is one of the main approaches to reduce model size and the number of flops
3

4. Motivation
● What if the underlying full-precision weights 𝑥 are clustered well around grids?
What about Cluster-Promoting Quantization?
4
Louizos et al., Relaxed Quantization for Discretized Neural Networks, ICLR 2019.
Not Clustered Clustered Well
Large Quantization Error
 Severe Performance
Degradation
Small Quantization Error
 Comparable Performance
to a full-precision network

5. Contribution
● Cluster-Promoting Quantization (CPQ)
● enables the underlying full-precision weights to be clustered well
● jointly finds the optimal quantization grids 𝒢 = 𝛼 −2𝑏−1
, ⋯ , 0, ⋯ , 2𝑏−1
− 1
according to clustered full-precision weights
● DropBits
● Our straight-through estimator (STE) in CPQ is biased like the original STE
● To compensate the defect of CPQ, we present a novel bit-drop technique, DropBits
● CPQ + DropBits
● CPQ + DropBits achieves the state-of-the-art results for ResNet-18 and
MobileNetV2 on the ImageNet dataset when all layers are uniformly quantized
5

6. Cluster-Promoting Quantization (CPQ)
● Our goal
● Given a weight 𝑥 and 𝒢 = 𝑔0, ⋯ , 𝑔2𝑏−1 = 𝛼 −2𝑏−1
, ⋯ , 0, ⋯ , 2𝑏−1
− 1 ,
● both (1) find the optimal 𝛼 and (2) cluster 𝑥 around 𝒢 cohesively in low bit-widths
● Without any regularization or loss for clustering, the key ingredients for our goal are
I. Probabilistic Parametrization for Quantization
II. Multi-Class Straight-Through Estimator
6

7. Cluster-Promoting Quantization (CPQ)
I. Probabilistic Parametrization for Quantization
● For each grid point 𝑔𝑖 ∈ 𝒢 = 𝑔0, ⋯ , 𝑔2𝑏−1 = 𝛼 −2𝑏−1
, ⋯ , 0, ⋯ , 2𝑏−1
− 1 ,
● compute the unnormalized probability that 𝑥 will be quantized to 𝑔𝑖 as follows:
𝜋𝑖 = 𝑝 𝑥 = 𝑔𝑖 𝑥, 𝛼, 𝜎 = Sigmoid
𝑔𝑖+
𝛼
2
−𝑥
𝜎
− Sigmoid
𝑔𝑖−
𝛼
2
−𝑥
𝜎
− 1
● where 𝑥, 𝛼, and 𝜎 are learnable parameters
● According to 𝝅 = 𝜋𝑖 𝑖=0
2𝑏−1
, design how to quantize 𝑥 to one of the grid points 𝒢
● (ex. Relaxed Quantization employed Gumbel-Softmax trick based on 𝝅)
7

8. Cluster-Promoting Quantization (CPQ)
II. Multi-Class Straight-Through Estimator (STE)
● Given 𝜋𝑖 = Sigmoid
𝑔𝑖+
𝛼
2
−𝑥
𝜎
− Sigmoid
𝑔𝑖−
𝛼
2
−𝑥
𝜎
, define a new STE as below:
𝐅𝐨𝐫𝐰𝐚𝐫𝐝: 𝑦 = one_hot argmax
𝑖
𝜋𝑖 − 2
𝐁𝐚𝐜𝐤𝐰𝐚𝐫𝐝:
𝜕ℒ
𝜕𝜋𝑖max
=
𝜕ℒ
𝜕𝑦𝑖max
and
𝜕ℒ
𝜕𝜋𝑖
= 0 for 𝑖 ≠ 𝑖max − 3
where 𝑦𝑖 is the 𝑖-th entry of the one-hot vector 𝑦, and 𝑖max = argmax
𝑖
𝜋𝑖
Our novel multi-class STE for clustering the underlying full-precision weights
8

9. Cluster-Promoting Quantization (CPQ)
II. Multi-Class Straight-Through Estimator (STE)
● With our novel multi-class STE, a full-precision parameter 𝑥 can be clustered
around its nearest quantization grid 𝑔𝑖max
once 𝑥 is trained to become near 𝑔𝑖max
9

10. Cluster-Promoting Quantization (CPQ)
II. Multi-Class Straight-Through Estimator (STE)
10

11. DropBits
● Unfortunately, our multi-class STE is biased to the mode like the original STE
● To reduce the bias of our STE, we propose a novel bit-drop method, ``DropBits’’
● Inspired by ``Dropout’’, drop an arbitrary number of grids at random every iteration
● DropBits can help reduce the bias of our multi-class STE in CPQ
11
Figure. The sampling distribution of CPQ is biased to the mode, −3α. With DropBits,
the sampling distribution of CPQ + DropBits resembles the original categorical distribution

12. Cluster-Promoting Quantization with DropBits (CPQ + DropBits)
● Experimental Results on the ImageNet dataset
CPQ + DropBits shows the state-of-the-art performance
12
3: Our own implementation with all layers quantized
Table. Top-1/Top-5 error (%) with ResNet-18 and MobileNetV2 on the ImageNet dataset.