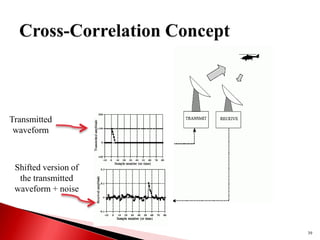
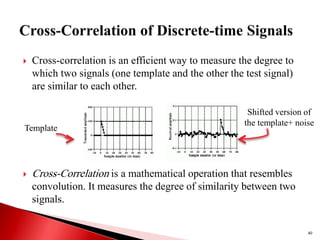
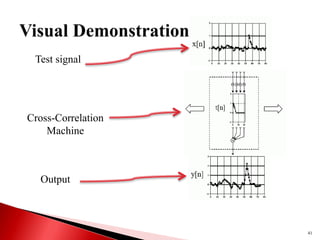
1) Discrete-time signals are functions of independent integer variables where samples are only defined at discrete time instants. 2) A discrete-time system transforms an input signal into an output signal through operations like addition, multiplication, delay. 3) Linear, time-invariant (LTI) systems have properties of superposition and time-invariance, and their behavior can be characterized by the impulse response. The output of an LTI system is the convolution of the input and impulse response.

2. 2
Our focus in the
next few lectures

3. 3
• A discrete-time signal is a function of independent integer variables.
• x(n) is not defined at instants between two successive samples.
• Sequence representation: ,...}
3
,
1
,
2
,
1
,
1
{
)
(

 
n
x
• Functional representation:


 

elsewhere
n
n
x
,
0
0
,
1
)
(

4. 4
Unit Sample Unit Step
Unit Ramp

5. 5
Exponential Signals: n
a
n
x n
all
for
)
( 

6.  Energy of Signals
6





2
|
)
(
| n
x
E 






N
N
n
N
n
x
N
P 2
|
)
(
|
1
2
1
lim
vs. Power of Signals

7. 7
 Periodic vs. aperiodic signals
 A signal is periodic with period N (N>0) iff
x(n+N)=x(n) for all n
 The smallest value of N where this holds is called the
fundamental period.
N

8.  Symmetric (even) and anti-symmetric (odd) signals:
◦ Even: x(-n) = x(n)
◦ Odd: x(-n) = -x(n)
 Any arbitrary signal can be expressed as a sum of two
signal components, one even and the other odd:
8
)
(
)
(
)
( n
x
n
x
n
x o
e 

=
+
 
)
(
)
(
)
( 2
1
n
x
n
x
n
xe 


 
)
(
)
(
)
( 2
1
n
x
n
x
n
xo 



9.  A discrete-time system is a device that performs some
operation on a discrete-time signal.
 A system transforms an input signal x(n) into an output
signal y(n) where: .
 Some basic discrete-time systems:
◦ Adders
◦ Constant multipliers
◦ Signal multipliers
◦ Unit delay elements
◦ Unit advance elements
9
)]
(
[
)
( n
x
T
n
y 

10. 10

11. 11

12. 12
Source: Stanford
)
2
(
)
( n
x
n
y 

13. 13
◦Addition: y(n) = x1(n) + x2(n)
◦Multiplication: y(n) = x1(n) x2(n)
◦Scaling: y(n) = a x(n)

14. 14


 



elsewhere
,
0
3
3
,
)
(
n
n
n
x )]
1
(
)
(
)
1
(
[
3
1
)
( 



 n
x
n
x
n
x
n
y
Moving average filter
}
0
,
3
,
2
,
1
,
0
,
1
,
2
,
3
,
0
{
)
( 



n
x
Solution:
3
2
]
1
0
1
[
3
1
)]
1
(
)
0
(
)
1
(
[
3
1
)
0
( 






 x
x
x
y
}
0
,
1
,
3
5
,
2
,
1
,
3
2
,
1
,
2
,
3
5
,
1
,
0
{
)
( 



n
y

15. 15


 



elsewhere
,
0
3
3
,
)
(
n
n
n
x ...]
)
2
(
)
1
(
)
(
[
)
( 




 n
x
n
x
n
x
n
y
Accumulator
}
0
,
3
,
2
,
1
,
0
,
1
,
2
,
3
,
0
{
)
( 



n
x
Solution:
}
12
,
12
,
9
,
7
,
6
,
6
,
5
,
3
,
0
{
)
( 



n
y

16.  Memoryless systems: If the output of the system at an
instant n only depends on the input sample at that time
(and not on past or future samples) then the system is
called memoryless or static,
e.g. y(n)=ax(n)+bx2(n)
 Otherwise, the system is said to be dynamic or to have
memory,
 e.g. y(n)=x(n)−4x(n−2)
16

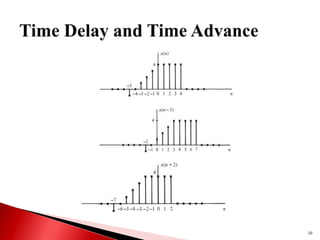
17.  In a causal system, the output at any time n only
depends on the present and past inputs.
 An example of a causal system:
y(n)=F[x(n),x(n−1),x(n− 2),...]
 All other systems are non-causal.
 A subset of non-causal system where the system
output, at any time n only depends on future inputs is
called anti-causal.
y(n)=F[x(n+1),x(n+2),...]
17

18.  Unstable systems exhibit erratic and extreme behavior.
BIBO stable systems are those producing a bounded
output for every bounded input:
 Example:
 Solution:
18






 y
x M
n
y
M
n
x )
(
)
(
)
(
)
1
(
)
( 2
n
x
n
y
n
y 

 Stable or unstable?
)
(
)
( n
C
n
x 
 Bounded signal
n
C
n
y
C
y
C
y
C
y 2
4
2
)
(
,...,
)
2
(
,
)
1
(
,
)
0
( 





 C
1 unstable

19.  Superposition principle:T[ax1(n)+bx2(n)]=aT[x1(n)]+bT[x2 (n)]
 A relaxed linear system with zero input
produces a zero output.
19
Scaling property
Additivity property

20.  Example:
 Solution:
 Example:
20
)
(
)
( 2
n
x
n
y 
)
(
)
( 2
1
1 n
x
n
y 
Linear or non-linear?
)
(
)
( 2
2
2 n
x
n
y 
)
(
)
(
))
(
)
(
(
)
( 2
2
2
2
1
1
2
2
1
1
3 n
x
a
n
x
a
n
x
a
n
x
a
T
n
y 



)
(
)
(
)
(
)
( 2
2
2
2
1
1
2
2
1
1 n
x
a
n
x
a
n
y
a
n
y
a 

 Linear!
)
(
)
( n
x
e
n
y 
1
)
(
0
)
( 

 n
y
n
x Non-linear!
Useful Hint: In a linear system, zero input results in a zero
output!

21.  If input-output characteristics of a system do not change with time then it is
called time-invariant or shift-invariant. This means that for every input
x(n) and every shift k
21
)
(
)
(
)
(
)
( k
n
y
k
n
x
n
y
n
x T
T








22.  Time-invariant example: differentiator
 Time-variant example: modulator
22
)
1
(
)
(
)
(
)
( 



 n
x
n
x
n
y
n
x T
)
2
(
)
1
(
)
1
(
)
1
( 






 n
x
n
x
n
y
n
x T
)
.
(
).
(
)
(
)
( 0 n
Cos
n
x
n
y
n
x T




x(n-1) T
¾ ®
¾ x(n-1).Cos(w0.n)
y(n-1)= x(n-1).Cos(w0.(n-1))
¹ y(n-1)

23.  LTI systems have two important characteristics:
◦ Time invariance: A system T is called time-invariant or shift-
invariant if input-output characteristics of the system do not
change with time
◦ Linearity: A system T is called linear iff
 Why do we care about LTI systems?
◦ Availability of a large collection of mathematical techniques
◦ Many practical systems are either LTI or can be approximated by LTI
systems.
23
)
(
)
(
)
(
)
( k
n
y
k
n
x
n
y
n
x T
T







T[ax1(n)+bx2(n)]=aT[x1(n)]+bT[x2 (n)]

24.  h(n): the response of the LTI system to the input unit sample
(n), i.e. h(n)=T((n))
An LTI system is completely characterized by a single impulse
response h(n).
y(n)=T[x(n)]= )
(
*
)
(
)
(
)
( n
h
n
x
k
n
h
k
x
k






Response of the system to the input
unit sample sequence at n=k
Convolution
sum
24

25. 25
Folding
Shifting
and
 




k
k
n
h
k
x
n
y )
(
)
(
)
(
Multiplying
 




k
k
n
h
k
x
n
y )
(
)
(
)
( 0
0
Repeat for all n0
Summation

26. 26
)
(
*
)
(
)
(
*
)
( n
x
n
h
n
h
n
x 
• Commutative law:
)]
(
2
*
)
(
)
(
1
*
)
(
)]
(
2
)]
(
1
[
*
)
( n
h
n
x
n
h
n
x
n
h
n
h
n
x 


 Distributive law:

27. 27
)]
(
2
*
)
(
1
[
*
)
(
)
(
2
*
)]
(
1
*
)
(
[ n
h
n
h
n
x
n
h
n
h
n
x 
 Associative law:

28. 28
)
(
2
1
)
(
1 n
u
n
h
n






 )
(
4
1
)
(
2 n
u
n
h
n






 ?
)
( 
n
h
• Solution:
 




k
k
n
h
k
h
n
h )
(
)
(
)
( 2
1
)
(
4
1
)
(
2
1
)
(
)
(
)
( 2
1 k
n
u
k
u
k
n
h
k
h
n
v
k
n
k
k 















 Non-zero for
0
,
0 

 k
n
k
0
,
0
)
( 
 n
n
h

















n
k
k
n
k
n
h
0 4
1
2
1
)
( 







n
k
k
n
0
2
4
1
0
),
1
2
(
)
4
1
( 1


 
n
n
n
 
 






1
0 1
1
n
k
n
k
r
r
a
ar

30.  Remember that for a causal system, the output at any point of time,
depends only on the present and past values of the input.
 In the case of an LTI system, causality is translated to a condition on
the impulse response. An LTI system is causal iff its impulse
response is zero for negative values of n , i.e. h(n)=0 for n<0
 This means that the convolution sum is modified to:
 Example: exponential input; h(n)=an u(n) with |a|<1
30

 







n
k
k
k
n
h
k
x
k
n
x
k
h
n
y )
(
)
(
)
(
)
(
)
(
0

31. 31
Causality Condition :
0
for
0
)
( 
 n
n
h






















0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
:
Proof
k
k
k
k
k
h
k
n
x
n
y
so
k
h
k
n
x
k
h
k
n
x
k
n
h
k
x
n
y
But x(n-k) for k>=0 shows
the past values of x(n). So y(n)
depends only on the
past values of x(n) and the
system is causal.
Neither necessary nor sufficient
condition for all systems, but
necessary and sufficient for LTI
systems
Causality in LTI Systems

32.  Stability: BIBO (bounded-input-bounded-output) stable
|x(n)|< => |y(n)|<
 In the case of an LTI system, stability is translated to a
condition on the impulse response too. An LTI system is stable
iff its impulse response is absolutely summable.
 This implies that the impulse response h(n) goes to zero as n
approaches infinity:
32
 





k
h k
h
S )
(

33. 33
Stability Condition : A linear time-invariant system is stable iff

















k
x
k
k
k
h
B
k
n
x
k
h
k
n
x
k
h
n
y
a ]
[
]
[
]
[
]
[
]
[
]
[
:
cy)
(Sufficien
)
output
unbounded
]
[
]
[
]
[
]
[
]
0
[
0
]
[
0
0
]
[
]
[
]
[
]
[
values
input with
the
Take
.
that
assume
us
Let
:
)
(Necessity
)
2
*

























h
k
k
h
S
k
h
k
h
k
h
k
x
y
n
h
n
h
n
h
n
h
n
x
S
b
Stability of LTI Systems







k
h k
h
S )
(

34. 34








0
,
0
,
)
(
n
b
n
a
n
h n
n a,b=? System Stable
• Solution: 


 








1
0
)
(
n
n
n
n
n
b
a
n
h
1
1
1
...
1
2
0
0





 







a
a
a
a
a
a
n
n
n
n
...)
1
1
1
(
1
1
2
1
1











 b
b
b
b
b
n
n
n
n
b
1

 










1
...)
1
( 2
)
1
1
( 
 b
or


35.  LTI systems can be divided into 2 types based on their impulse response:
 An FIR system has finite-duration h(n), i.e. h(n) = 0 for n < 0 and n ≥ M.
 This means that the output at any time n is simply a weighted linear
combination of the most recent M input samples (FIR has a finite memory
of length M).
 An IIR system has infinite-duration h(n), so its output based on the
convolution formula becomes (causality assumed)
 In this case, the weighted sum involves present and all past input samples
thus the IIR system has infinite memory.
35
 



1
0
)
(
)
(
)
(
M
k
k
n
x
k
h
n
y
 


0
)
(
)
(
)
(
k
k
n
x
k
h
n
y

36.  FIR systems can be readily implemented by their convolution
summation (involves additions, multiplications, and a finite
number of memory locations).
 IIR systems, however, cannot be practically implemented by
convolution as this requires infinite memory locations,
multiplications, and additions.
 However, there is a practical and computationally efficient
means for implementing a family of IIR systems through the
use of difference equations.
36

37.  Cumulative Average System:
37
 



n
k
n
k
x
n
n
y
0
,...
1
,
0
),
(
1
1
)
(
)
(
)
(
)
(
)
1
(
1
0
n
x
k
x
n
y
n
n
k






)
(
)
1
( n
x
n
ny 


)
(
1
1
)
1
(
1
)
( n
x
n
n
y
n
n
n
y





+ Initial Condition






1
0
,...
1
,
0
),
(
1
)
1
(
n
k
n
k
x
n
n
y

39. 39
Shifted version of
the transmitted
waveform + noise
Transmitted
waveform

40.  Cross-correlation is an efficient way to measure the degree to
which two signals (one template and the other the test signal)
are similar to each other.
 Cross-Correlation is a mathematical operation that resembles
convolution. It measures the degree of similarity between two
signals.
Template
Shifted version of
the template+ noise
40

41. 41
Test signal
Cross-Correlation
Machine
Output

42. 42
• Applications include radar, sonar, biomedical signal processing and
digital communications.
• The amplitude of each sample in the cross-
correlation signal is a measure of how much
the received signal resembles the target
signal, at that location.
• The value of the cross-correlation is
maximized when the target signal is aligned
with the same features in the received signal.
• Using cross-correlation to detect a known
waveform is frequently called matched filtering.

43. 43
)
(
)
(
)
( n
D
n
x
n
y 
 


)
(n
x Transmitted/Desired Signal
Received/Test Signal
Delayed version
of the input
Additive noise
Attenuation factor
 



 




 



 n
n
xy l
n
y
l
n
x
l
n
y
n
x
l
r ,...
2
,
1
,
0
),
(
)
(
)
(
)
(
)
(
• ryx(l) is thus the folded version of rxy(l) around l = 0 :
)
(
)
( l
r
l
r yx
xy 


44. 44
• Cross-correlation involves the same
sequence of steps as in convolution except the
folding part, so basically the cross-correlation
of two signals involves:
1. Shifting one of the sequences
2. Multiplication of the two sequences
3. Summing over all values of the product

45.  The cross-correlation machine and convolution machine are
identical, except that in the correlation machine this flip
doesn't take place, and the samples run in the normal
direction.
 Convolution is the relationship between a system's input
signal, output signal, and the impulse response. Correlation
is a way to detect a known waveform in a noisy
background.
 The similar mathematics is only a convenient coincidence.
45
)
(
*
)
(
)
( l
y
l
x
l
rxy 
 Cross-correlation is
non-commutative.

46. 46
)
(
)
(
)
(
)
(
)
(
)
(
l
r
n
x
l
n
x
l
n
x
n
x
l
r
xx
n
n
xx


 

 








47.  It can be shown that:
 For autocorrelation, we thus have:
 This means that autocorrelation of a signal attains its
maximum value at zero lag (makes sense as we expect
the signal to match itself perfectly at zero lag).
47
y
x
yy
xx
xy E
E
r
r
l
r 
 )
0
(
)
0
(
)
(
x
xx
xx E
r
l
r 
 )
0
(
)
(

48.  If signals are scaled, the shape of the cross-correlation
sequence does not change. Only the amplitudes are scaled.
 It is often desirable to normalize the auto-correlation and
cross-correlation sequences to a range from -1 to 1.
 Normalized autocorrelation:
 Normalized cross-correlation:
48
)
0
(
)
(
)
(
xx
xx
xx
r
l
r
l 

)
0
(
)
0
(
)
(
)
(
yy
xx
xy
xy
r
r
l
r
l 


49. In this lecture, we learned about:
 Representations of discrete time signals and common basic DT signals
 Manipulation and representations/diagrams of DT systems
 Various classification of DT signals:
 Periodic vs. non-periodic, symmetric vs. anti-symmetric
 Classifications of DT systems:
◦ Static vs. dynamic, time-invariant vs. time-variant, linear vs. non-linear, causal vs.
◦ non-causal, stable vs. non-stable, FIR vs. IIR
 LTI systems and their representation
 Convolution for determining response to arbitrary inputs
 Cross-correlation
49