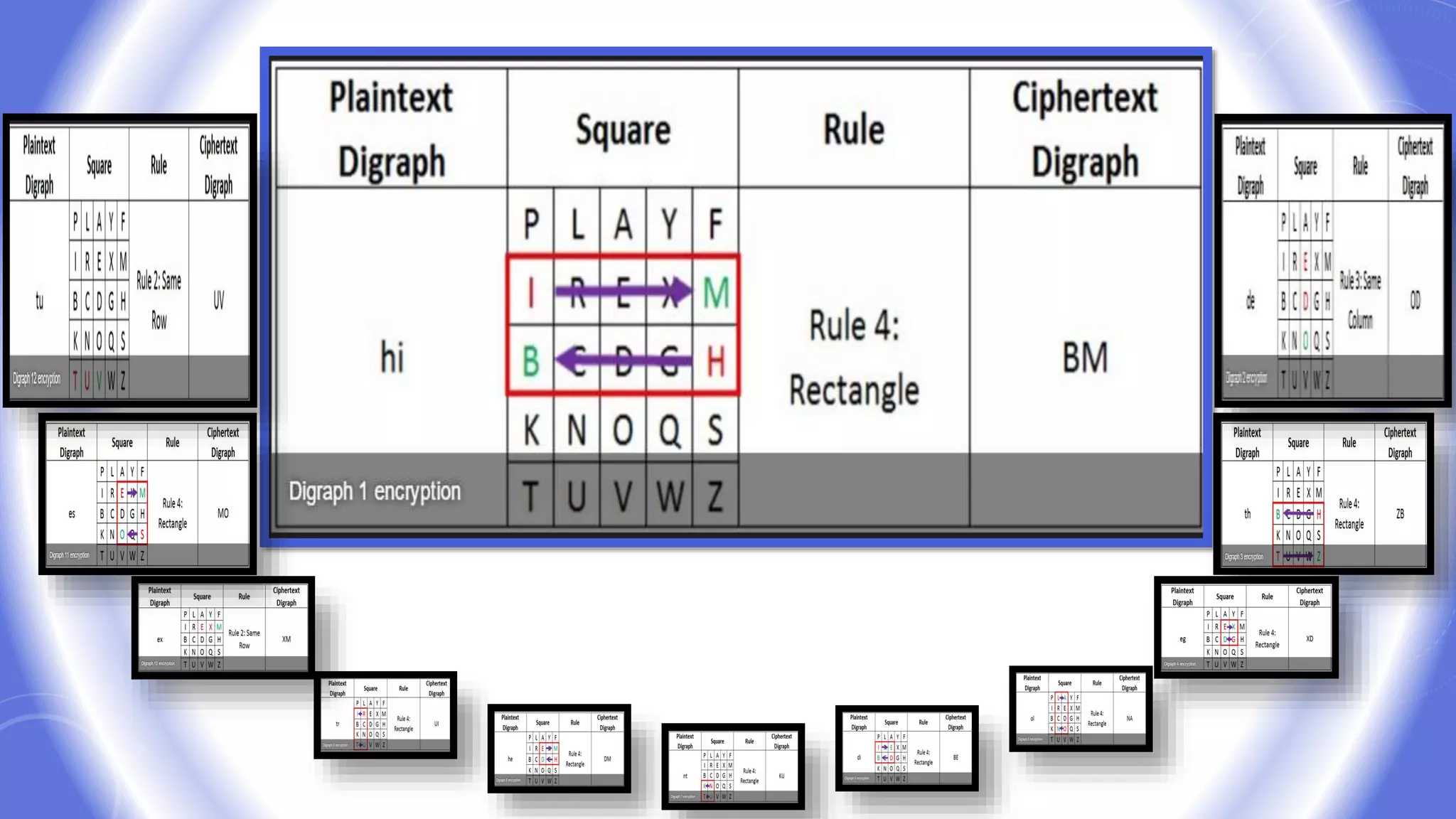
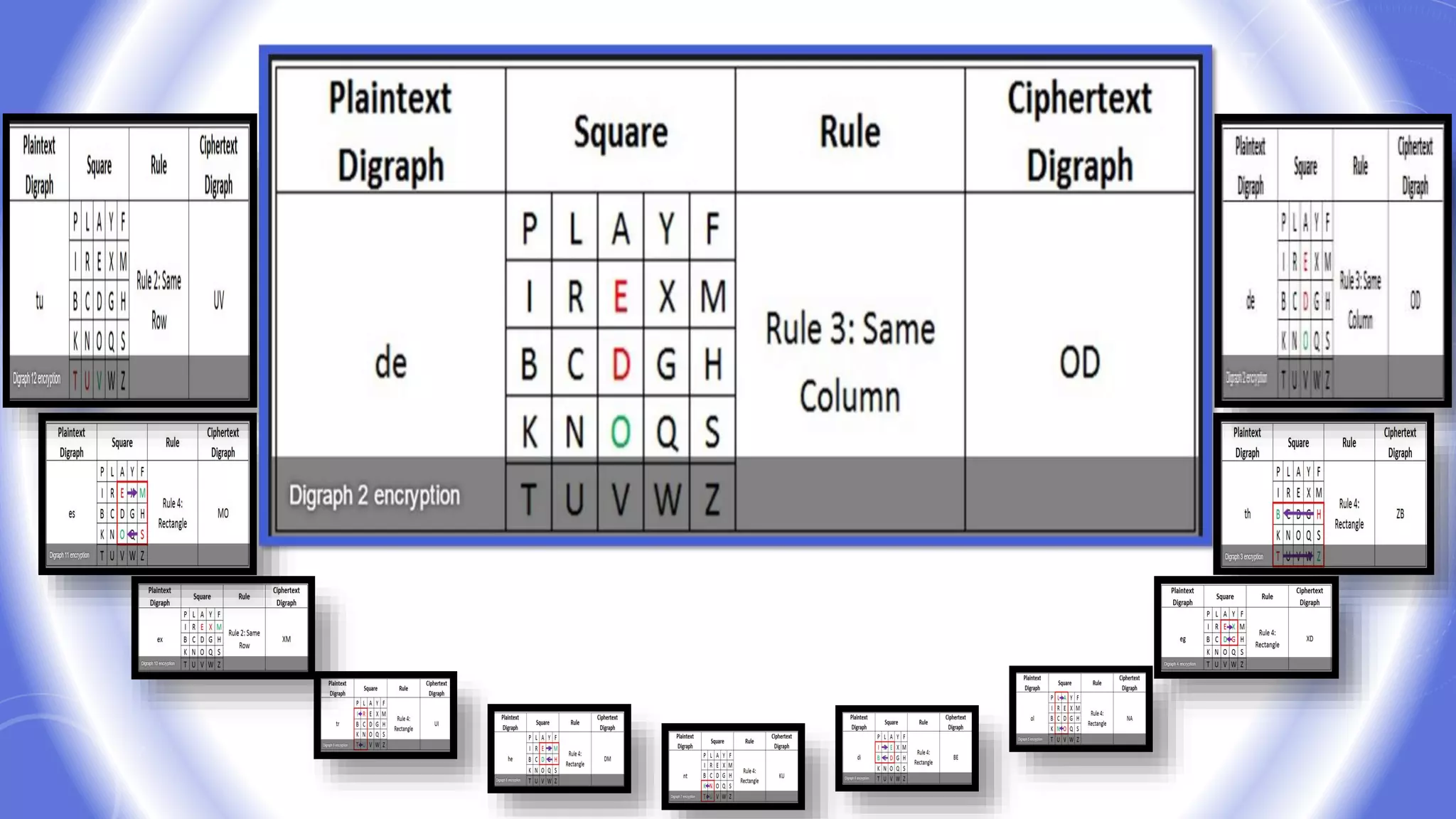
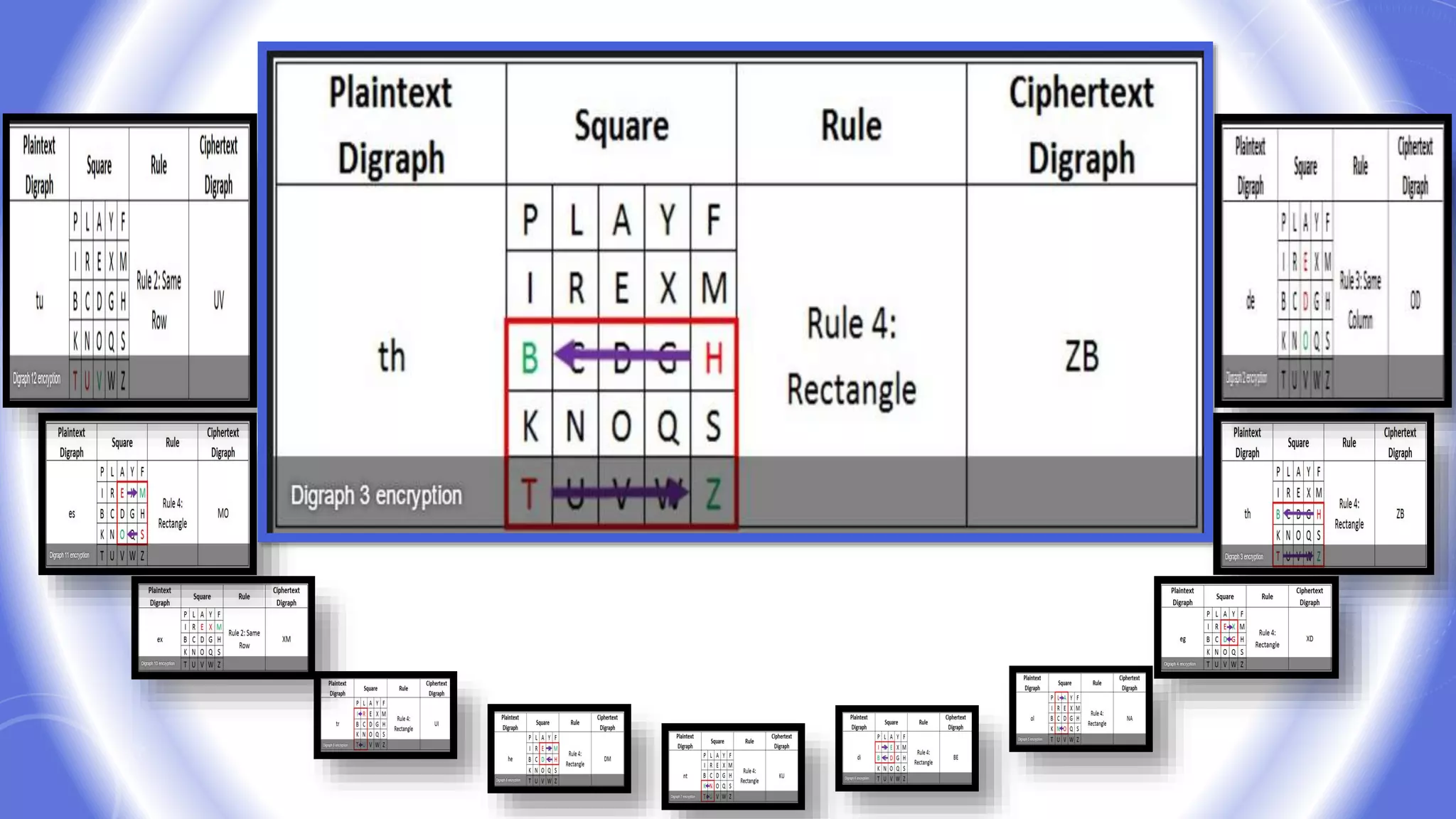
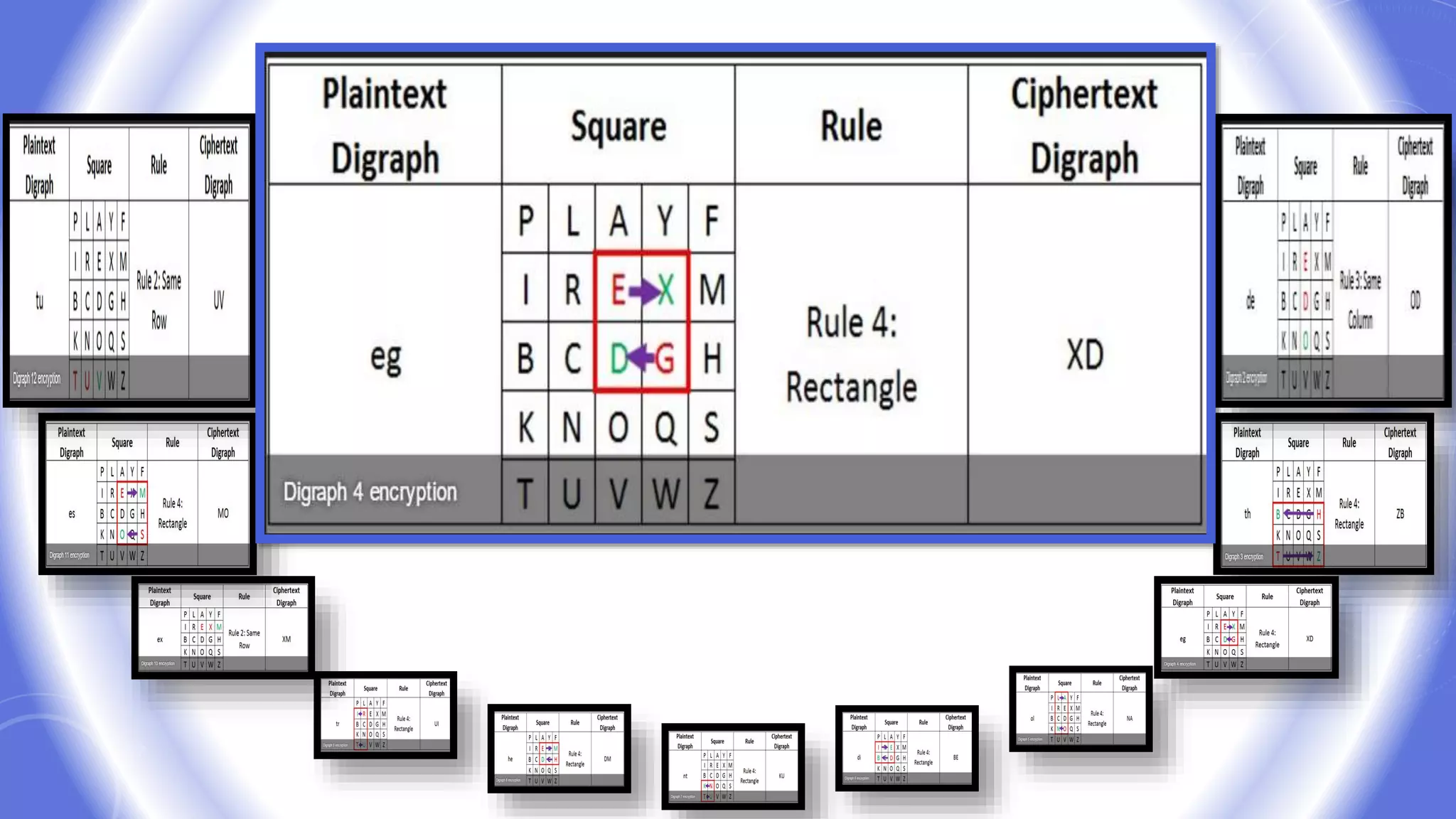
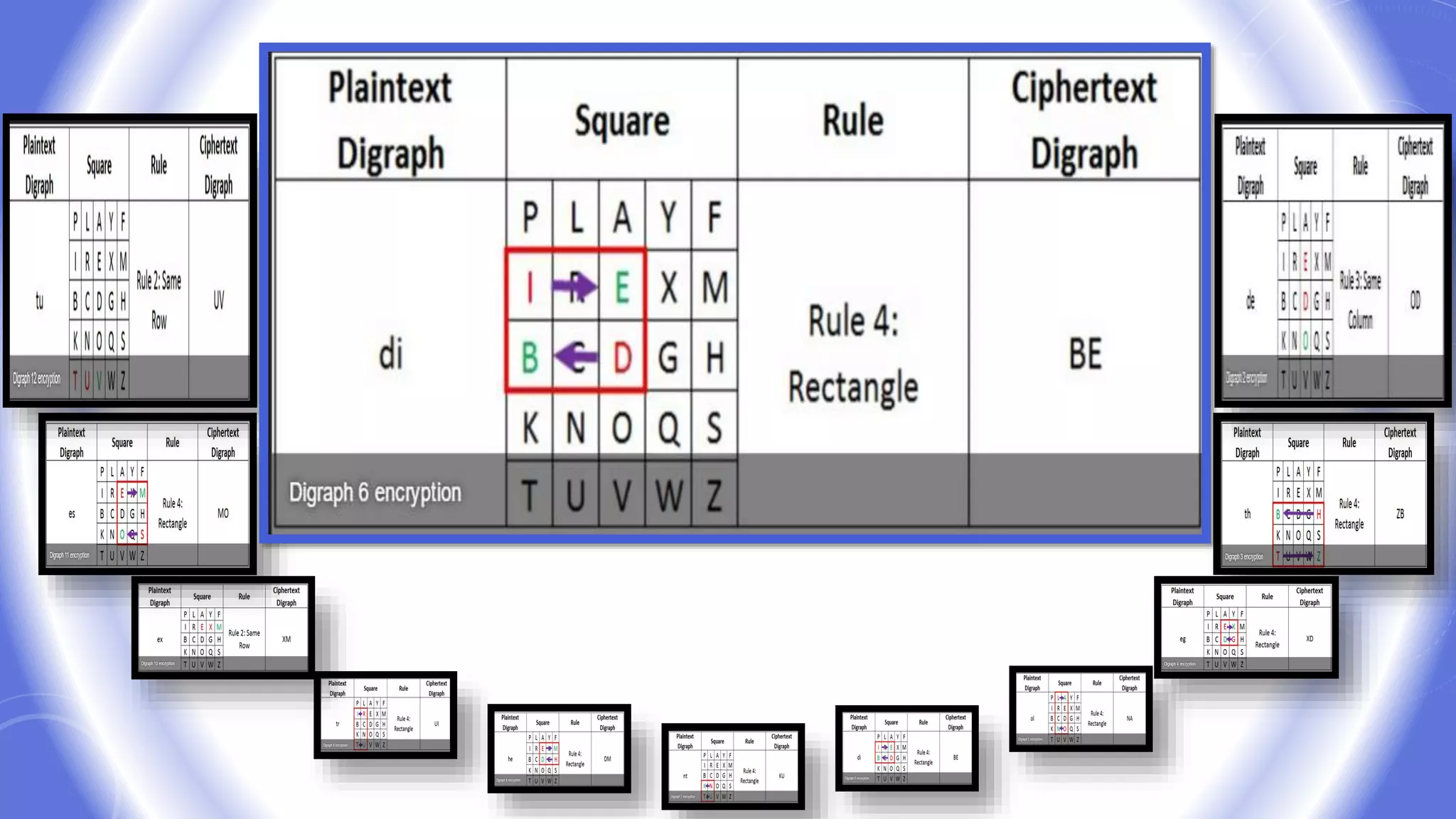
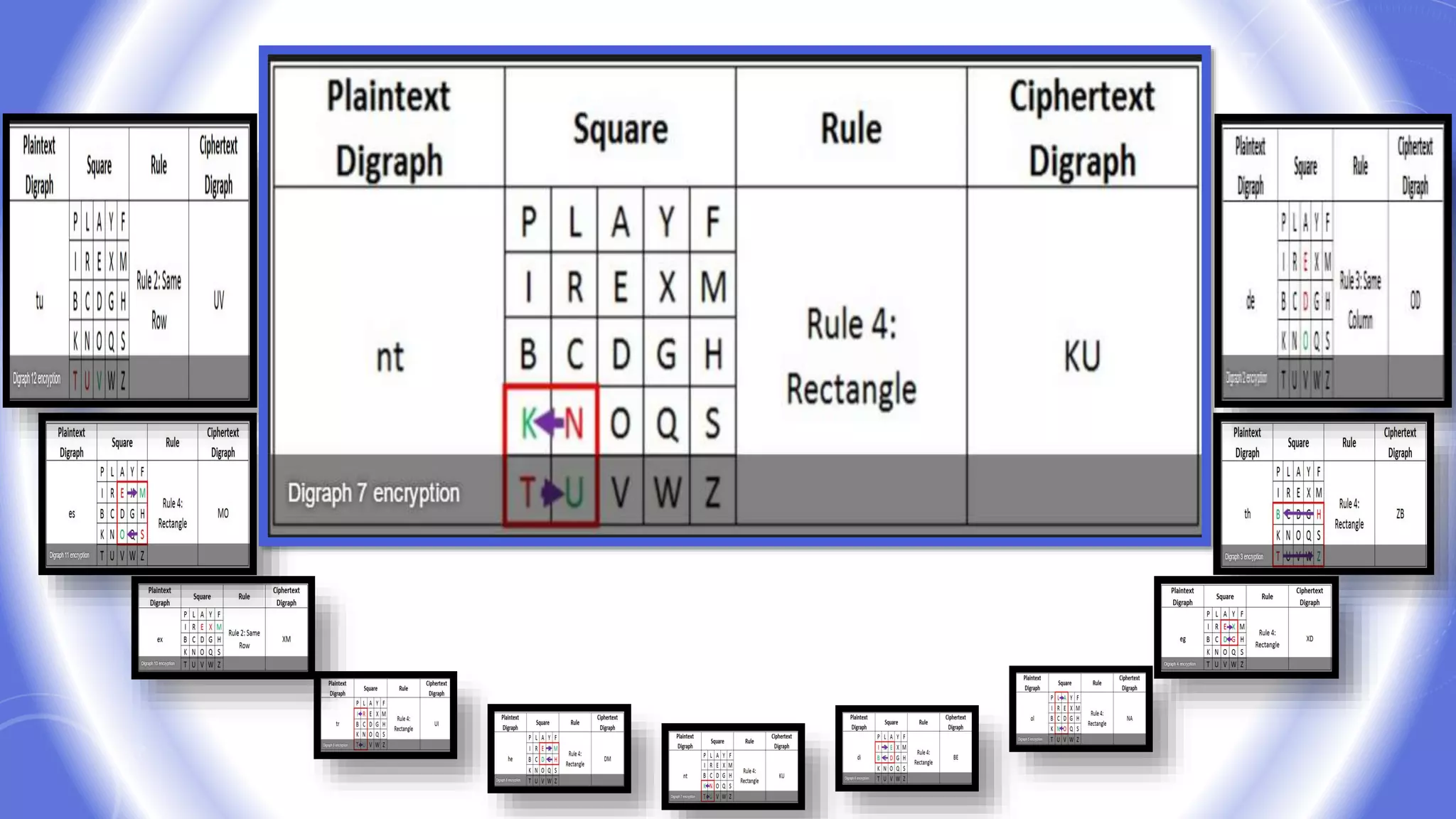
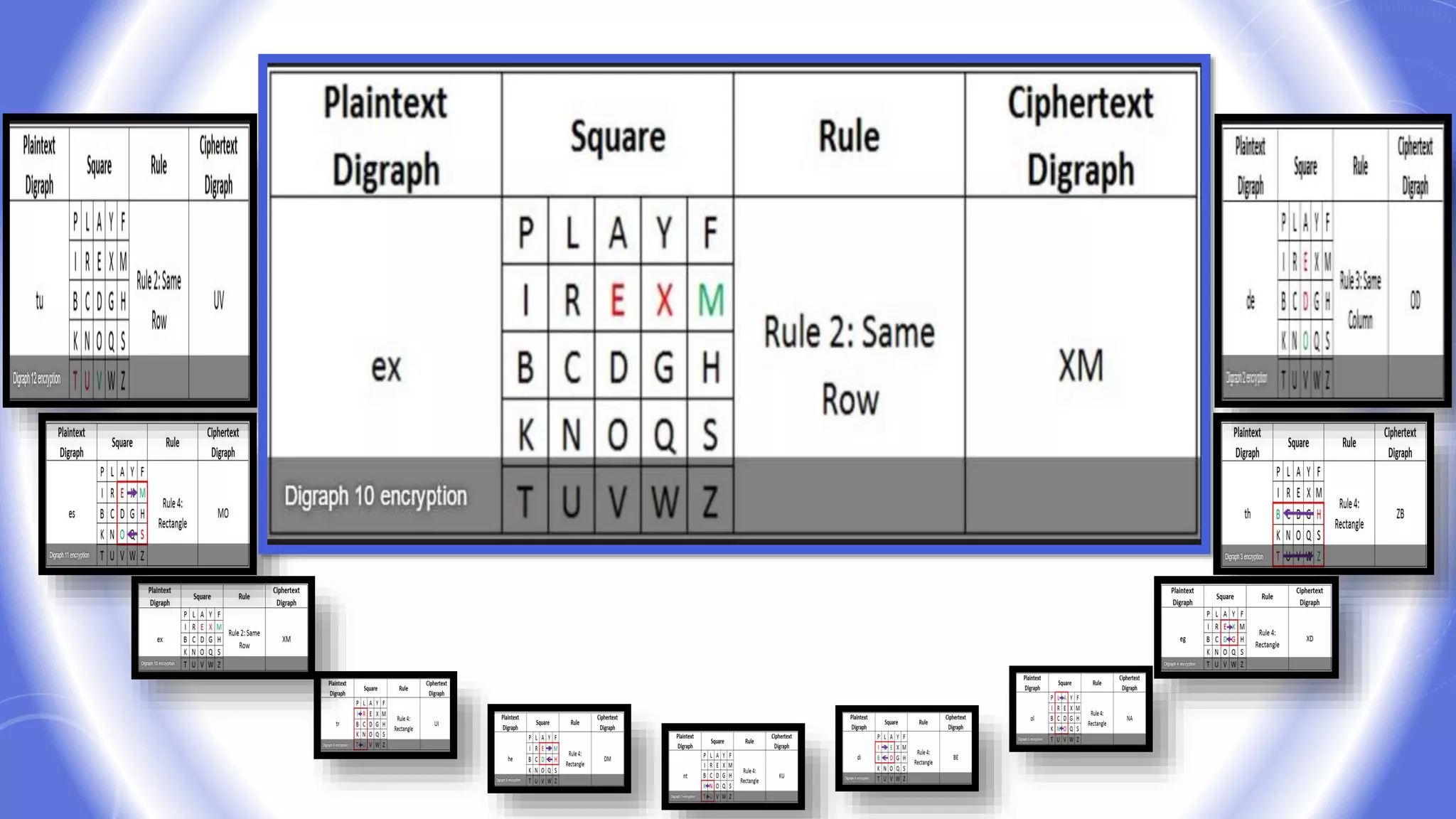
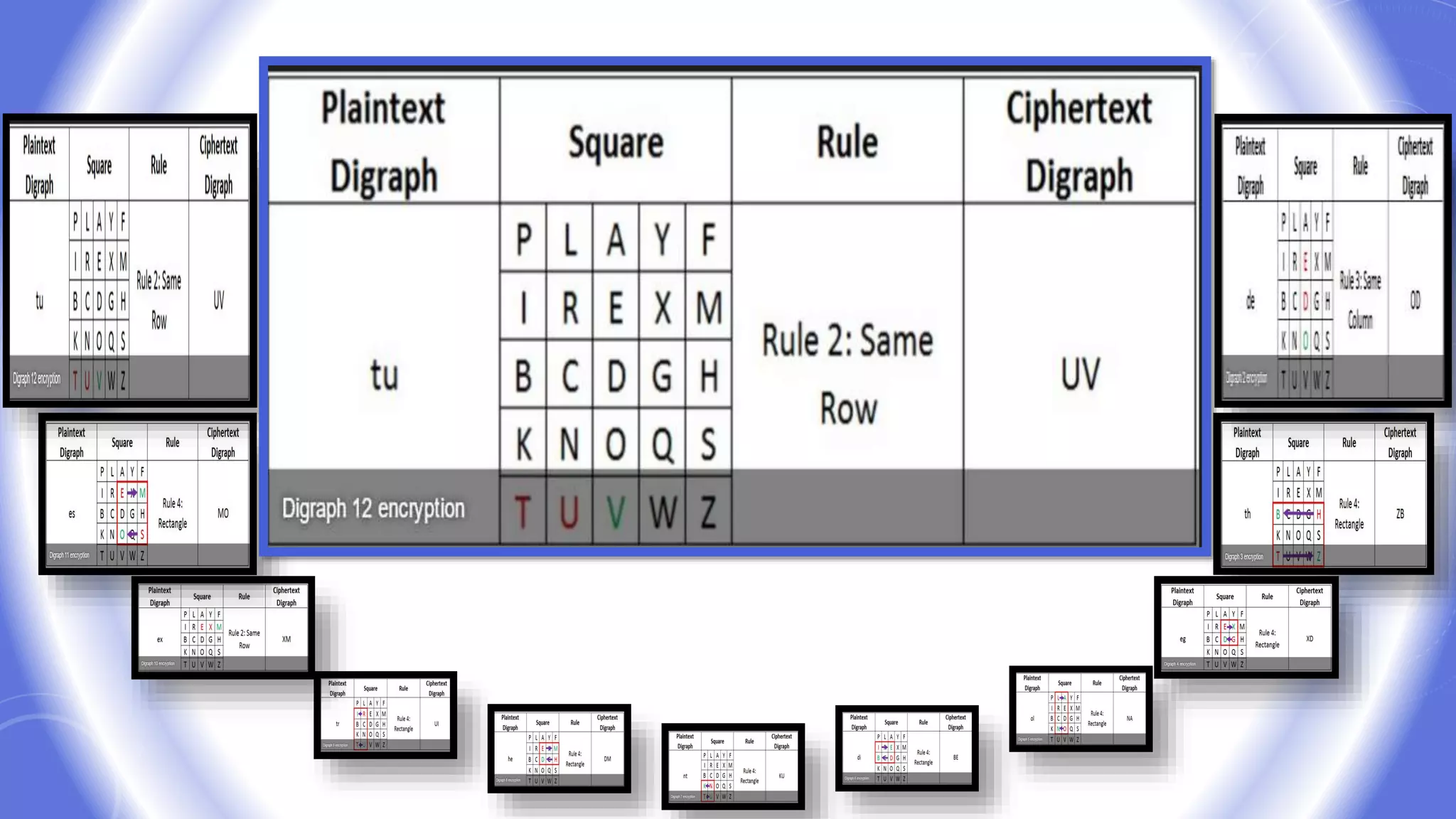
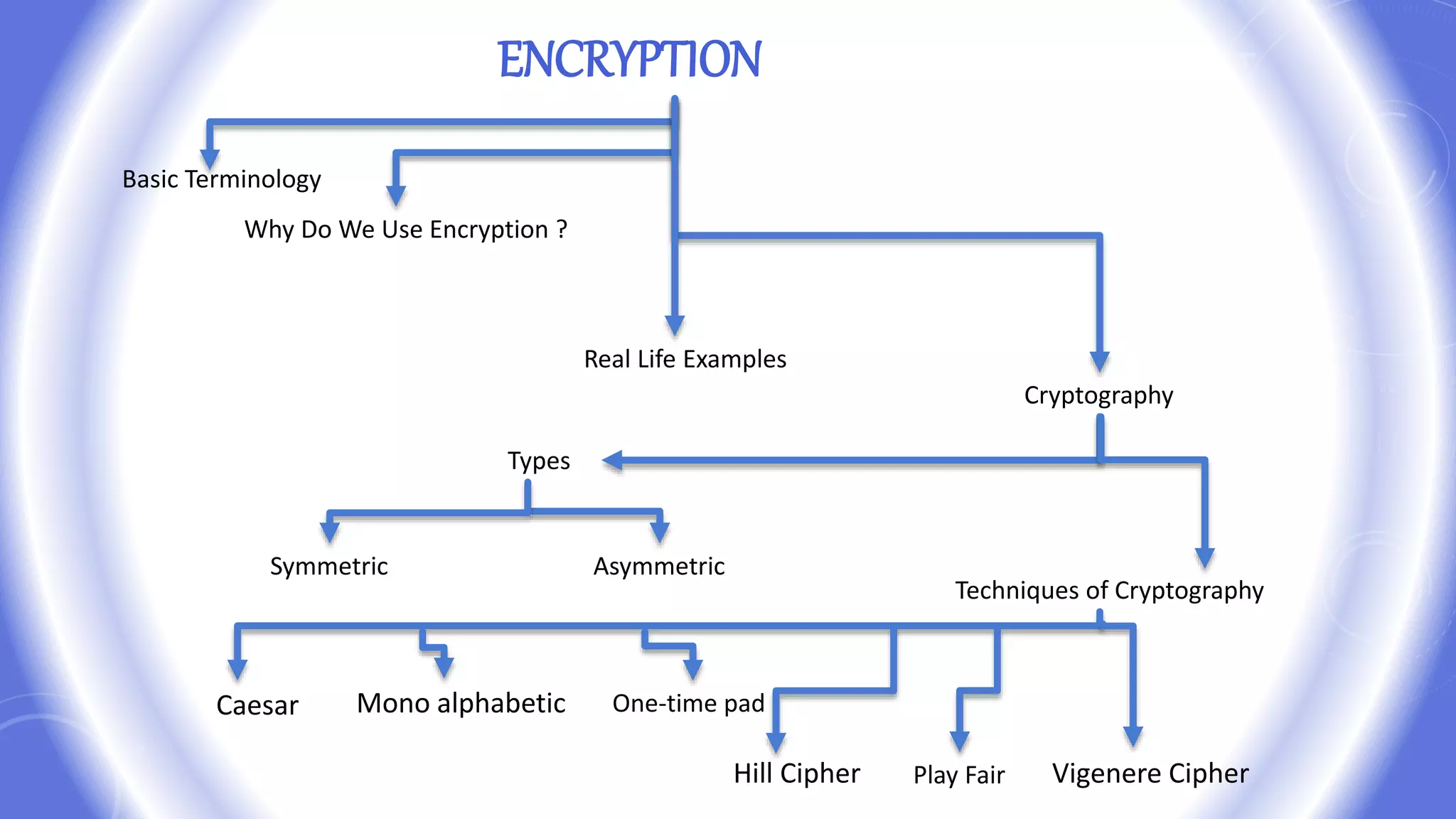
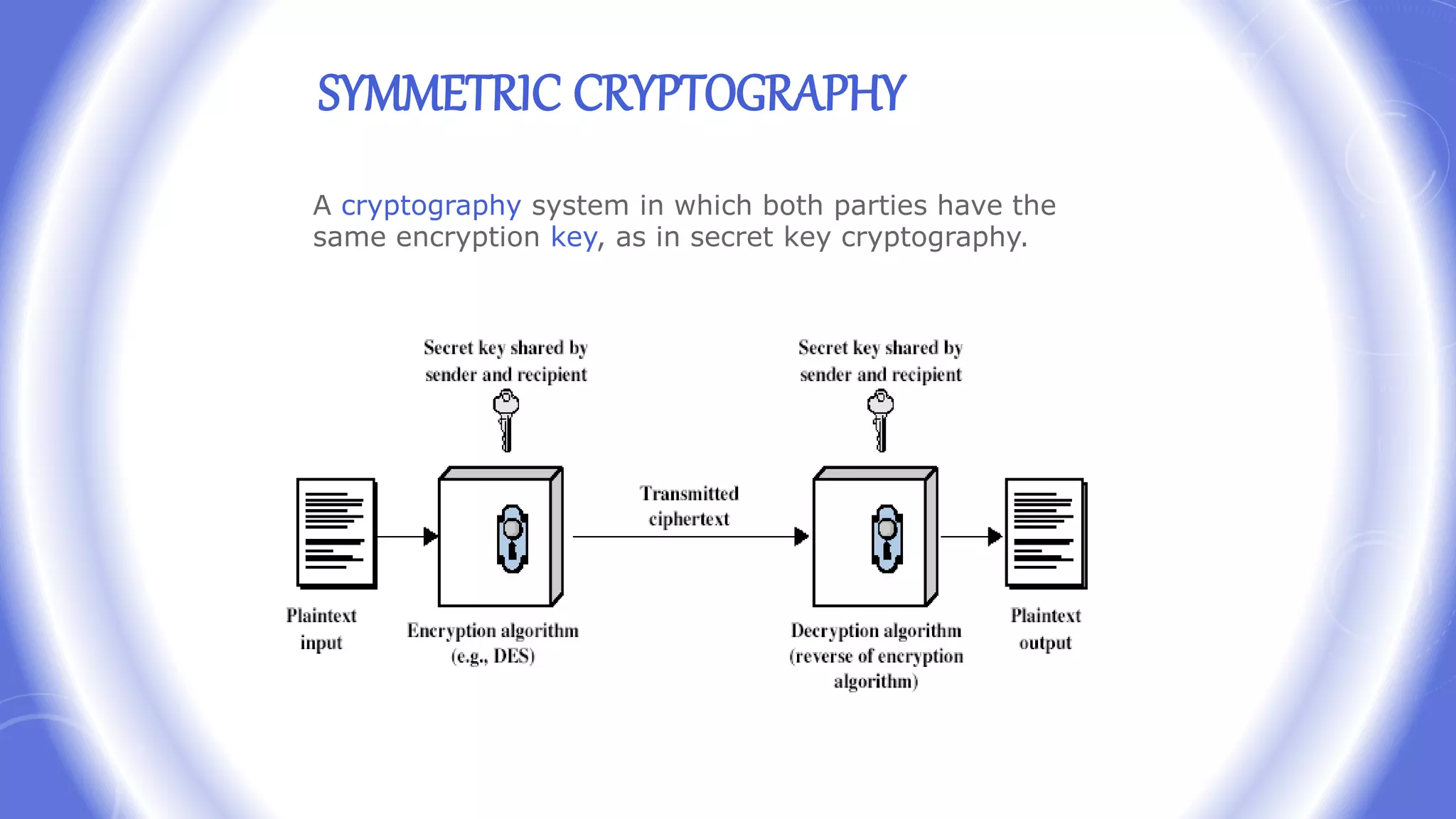
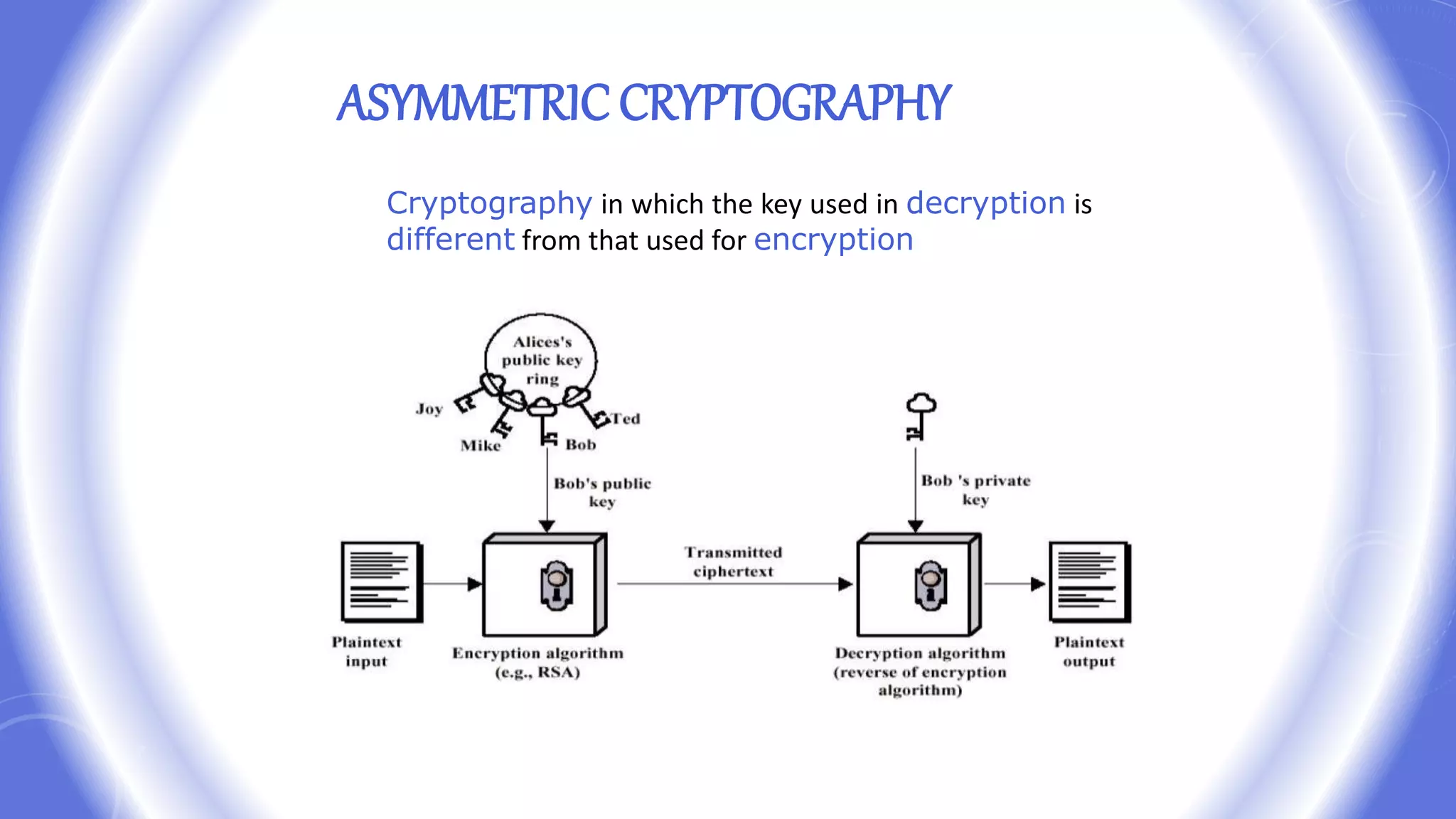
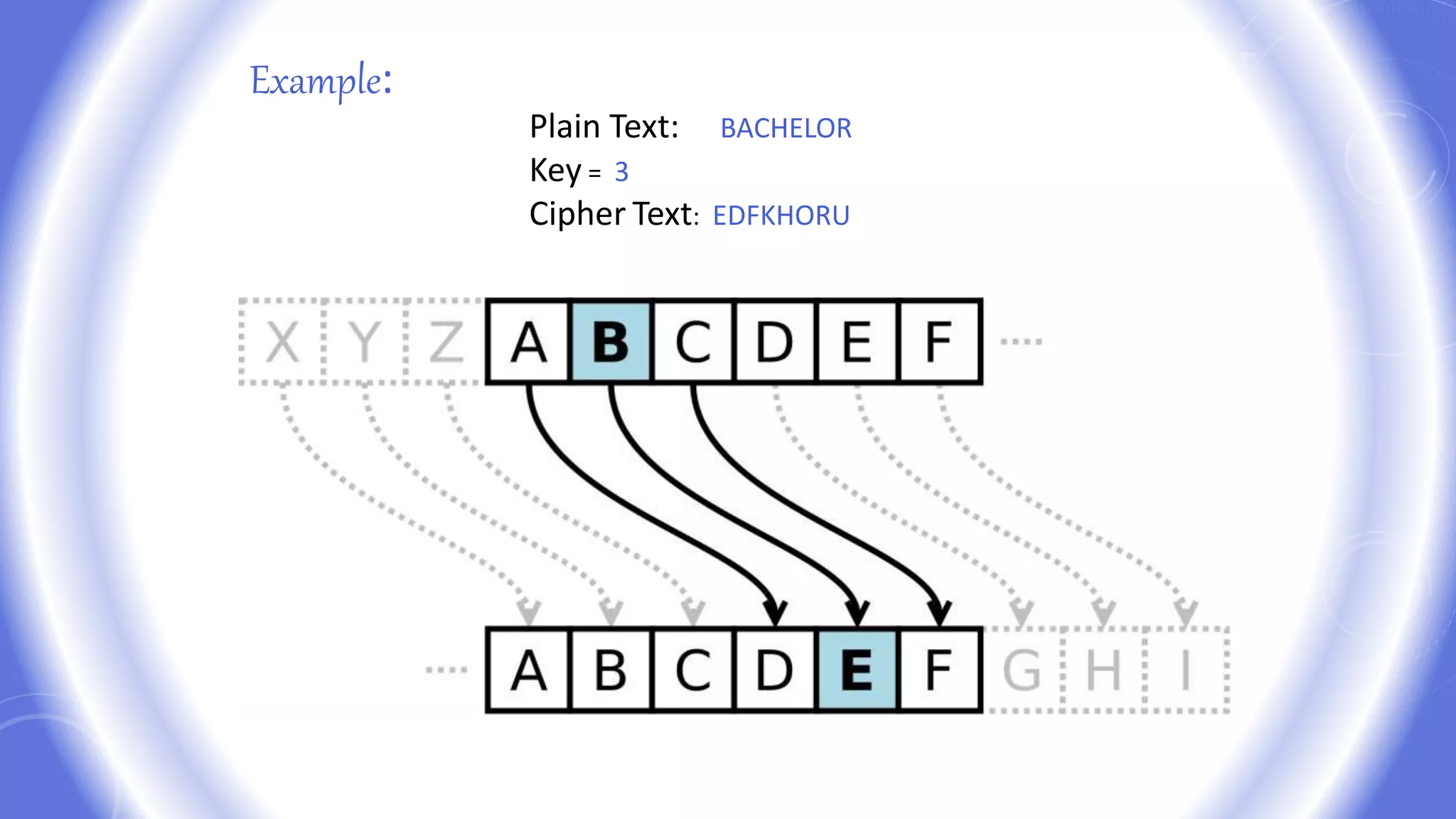
This document provides an overview of encryption techniques. It begins with basic terminology used in cryptography such as plaintext, ciphertext, cipher, key, enciphering, deciphering, and cryptanalysis. It then discusses why encryption is used and provides real-life examples of encryption applications. The document outlines symmetric and asymmetric cryptography and describes several classical ciphers such as the Caesar cipher, monoalphabetic ciphers, the one-time pad, Hill cipher, Playfair cipher, and Vigenere cipher.

2. Amad Khadim
Zubair Farooq
Subject :
EncryptionTopic :
Presented by :
Network Security

3. ROAD MAP

4. ENCRYPTION
Basic Terminology
Why Do We Use Encryption ?
Real Life Examples
Cryptography
Types
Symmetric Asymmetric
Caesar Mono alphabetic One-time pad
Hill Cipher Play Fair Vigenere Cipher
Techniques of Cryptography

5. Plaintext:
The original message
Ciphertext:
The coded message
Cipher:
Algorithm for transforming plaintext to ciphertext.
Key:
Info used in cipher known only to sender/receiver.
BASIC CONCEPTS
Encipher (encrypt):
Converting plaintext to ciphertext.
Decipher (decrypt):
Recovering ciphertext from plaintext.
Cryptography :
Study of encryption principles/methods.
Cryptanalysis (code breaking):
The study of principles/ methods of deciphering ciphertext without
knowing key.
Cryptology:
The field of both cryptography and cryptanalysis

6. WHY DO WE USE ENCRYPTION?
 To secure important information
e.g.
 Files on computers
 Data being passed through the Internet
 ATM machines
 E-Commerce
 Credit card information
Etc.
 Prevents information from getting stolen or read
 Without encryption, there is no reliable security

7. REAL LIFE EXAMPLES
 Used in the military and the government
 Now used in everyday life:
 Online banking
 E-commerce
 Student records, health records, tax records etc.
 ATM machines
 Social networking (emails, texts, instant messengers)
 Businesses

8. SYMMETRIC CRYPTOGRAPHY
A cryptography system in which both parties have the
same encryption key, as in secret key cryptography.

9. ASYMMETRIC CRYPTOGRAPHY
Cryptography in which the key used in decryption is
different from that used for encryption

10.  To pass an encrypted message from one person to another, it is first
necessary that both parties have the 'key' for the cipher
 Encryption Method: C = P + K Key = 3
 Decryption Method: P = C - K Key = 3
CAESAR CIPHER
Caesar Cipher is One of the simplest examples of a substitution cipher, which
have been used by Julius Caesar to communicate with his army.

11. Example:
Plain Text: BACHELOR
Key = 3
Cipher Text: EDFKHORU

12. Monoalphabetic Ciphers
 The substitution is fixed for each letter of the alphabet.
 Thus, if "a" is encrypted to "R", then every time we see the letter "a" in the plaintext,
we replace it with the letter "R" in the ciphertext.
 A simple example is where each letter is encrypted as the next letter in the alphabet:
"a simple message“.
Plain Text:” a simple message “
Cipher Text: B TJNQMF NFTTBHF
A monoalphabetic cipher, also known as a simple substitution
cipher, relies on a fixed replacement structure.

13. One-time Pad Ciphers
 The one-time pad is a long sequence of random letters.
 These letters are combined with the plaintext message to produce the cipher
text.
 To decipher the message, a person must have a copy of the one-time pad to
reverse the process.
 A one-time pad should be used only once (hence the name) and then
destroyed.
 To encipher a message, you take the first letter in the plaintext message and add
it to the first random letter from the one-time pad.

14.  Suppose you are enciphering the letter S (the 19th letter of the alphabet) and
the one-time pad gives you C (3rd letter of the alphabet).
 You add the two letters and subtract 1.
 When you add S and C and subtract 1, you get 21 which is U.
 Each letter is enciphered in this method.
One-time Pad Example
Plaintext : SECRETMESSAGE
One-time pad: CIJTHUUHMLFRU
Ciphertext : UMLKLNGLEDFXY

15. Hill Ciphers
 The Hill Cipher was invented by Lester S. Hill in 1929.
 It can work on digraphs (2X2), trigraphs (3X3) or theoretically
any sized blocks.
 The Hill Cipher uses an area of mathematics called Linear
Algebra.
 It also makes use of Modulo Arithmetic.
 The cipher has a significantly more mathematical nature than
some of the others ciphers.

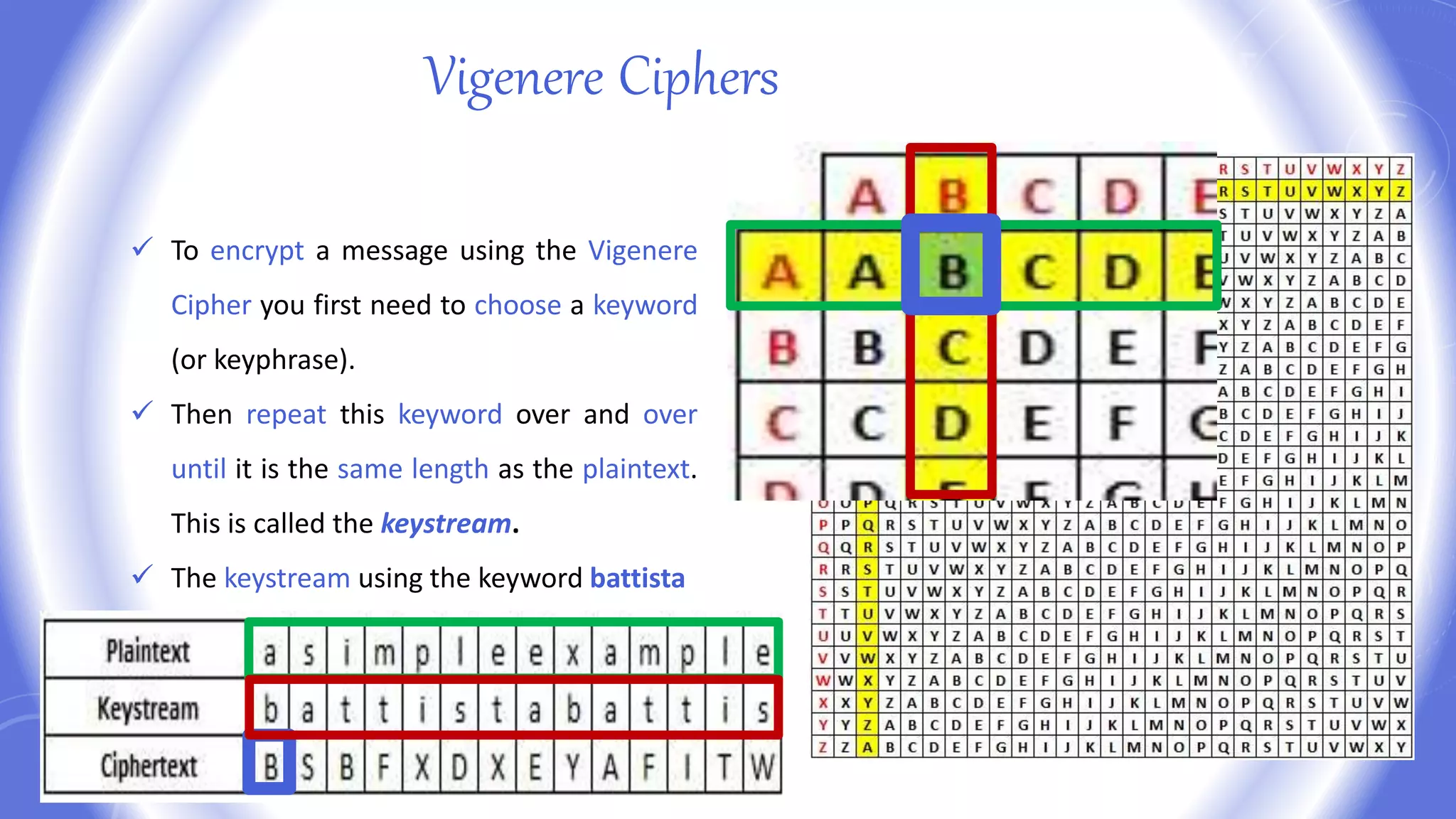
16. Hill Cipher Example
The key for a hill cipher is a matrix
e.g.
 In the above case, we have taken the size to be 3×3
 Assume we want to encipher the message ATTACK AT DAWN.
 We now take the first 3 characters from our plaintext, ATT and
create a vector that corresponds to the letters to get: [0 19 19]
Hill Ciphers example

17. Playfair Ciphers
 Invented by Charles Wheatstone in 1854, but named after his friend
Baron Playfair.
 In order to encrypt using the Playfair Cipher, we must first draw up
a Polybius Square.
 Its providing a stronger cipher than a Monoalphabetic Cipher.
 Playfair Cipher is the best known such cipher.

18. Playfair Key Matrix
 Use a 5 x 5 matrix.
 Fill in letters of the key (combine "I" and "J"
in the square).
 Fill the rest of matrix with other letters.
 E.g. key = PLAYFIRE.

19. Playfair Rules
Plaintext is encrypted two letters at a time.
 If a pair is a repeated letter, insert filler like 'X’.
 If both letters fall in the same row, replace each with the letter to
its right (circularly).
 If both letters fall in the same column, replace each with the
letter below it (circularly).
 Otherwise, each letter is replaced by the letter in the same row
but in the column of the other letter of the pair.

20. “hide the gold in the tree stump”Plain Text :
 Rule 1, and split up any double letter digraphs by inserting an "x"
between them.
 The first image below shows the initial digraph split of the plaintext, and
the second image displays how we split up the "ee" into "ex" and "es".
 The digraph split once we apply Rule 1, and remove any digraphs made from two of the same letter.
Playfair Example

33.  The Vigenere cipher, was invented by a Frenchman, Blaise de
Vigenere in the 16th century.
 The Vigenere cipher uses a 26×26 table with A to Z as the row
heading and column heading.
 This table is usually referred to as the Vigenere Tableau, Vigenere
Table or Vigenere Square.
Vigenere Ciphers

34. Vigenere Cipher Table

35. Vigenere Ciphers
 To encrypt a message using the Vigenere
Cipher you first need to choose a keyword
(or keyphrase).
 Then repeat this keyword over and over
until it is the same length as the plaintext.
This is called the keystream.
 The keystream using the keyword battista