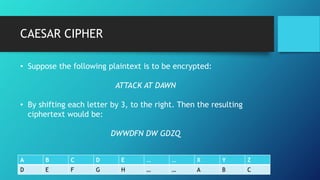
The Caesar cipher is one of the earliest known substitution ciphers. It works by shifting each letter in a plaintext message by a set number of positions (the key) in the alphabet to encrypt it. For example, with a key of 3, A would be replaced by D, B by E, and so on. Decryption simply requires shifting letters in the opposite direction by the same key. While simple, the Caesar cipher has some mathematical properties and was allegedly used by Julius Caesar to communicate with his army. However, it is also easy to break through brute force by trying all 26 possible keys.

1. CAESAR CIPHER
Cryptography & Cryptanalysis
Ramadhi Irawan

2. DEFINITION
• Plaintext
• Is a message to be communicated.
• Ciphertext
• A disguided version of a plaintext.
• Encryption
• The process of turning Plaintext into Ciphertext.
• Decryption
• The process of turning Ciphertext into Plaintext.
• Encipher / Decipher
• Are synonymous with the verb encrypt & decrypt.

3. DEFINITION
• Cryptology
• The study of encryption and decryption.
• Cryptography
• The application of Cryptology.

4. CAESAR CIPHER
• One of the earliest known example of substitution cipher.
• Said to have been used by Julius Caesar to communicate with his
army (secretly).
• Each character of a plaintext message is replaced by a character n
position down in the alphabet.
• Belongs to Substitution Cipher

5. CAESAR CIPHER
A B C D E … … X Y Z
D E F G H … … A B C
• Example:
• First row denotes the plaintext
• Second row denotes the ciphertext
• Ciphertext is obtain by “shifting” the orginal letter by N
position to the right.
• In This example, it is shifted by 3 to the right.
• A becomes D
• B becomes E
• X becomes A, and so on…

6. CAESAR CIPHER
A B C D E … … X Y Z
D E F G H … … A B C
• Suppose the following plaintext is to be encrypted:
ATTACK AT DAWN
• By shifting each letter by 3, to the right. Then the resulting
ciphertext would be:
DWWDFN DW GDZQ

7. CAESAR CIPHER
• One could shift other than 3 letters apart.
• The offset (Number of shift) is called the “Key”
• Decryption Process:
• Given that the key is known, just shift back N letter to the left.
• Example:
• Ciphertext:
WJYZWS YT GFXJ
• Key used: 3
• Plaintext:
RETURN TO BASE

8. CAESAR CIPHER
• Math behind this:
• Can be represented using modular arithmetic
• Assume that :
• A = 0, B = 1, C = 2, …, Y = 24, Z = 25
• Encryption process can be represented as:
• Such that:
• X  the plaintext.
• k  the number of shift (offset).
• 26  There are 26 letters in the alphabet (English
alphabet).

9. CAESAR CIPHER
• Math behind this:
• Can be represented using modular arithmetic
• Assume that :
• A = 0, B = 1, C = 2, …, Y = 24, Z = 25
• Decryption process can be represented as:
• Such that:
• X  the plaintext.
• k  the key (number of shift or offset).
• 26  There are 26 letters in the alphabet (English
alphabet).

10. CAESAR CIPHER
• Summary
• Considerably easy to break.
• Brute force attack works pretty well, due to relatively small
keys (only allows 26 different keys).
• Also known as monoalphabetic cipher, which the same plaintext
letters are always replaced by the same ciphertext letters.
• Mono – means one, indicates that each letter has a single
substitute.