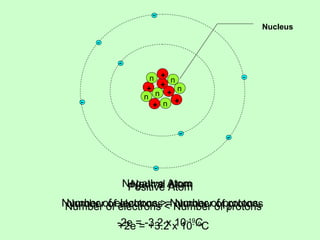
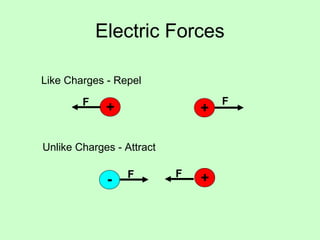
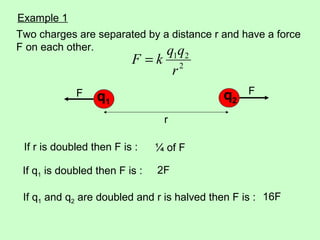
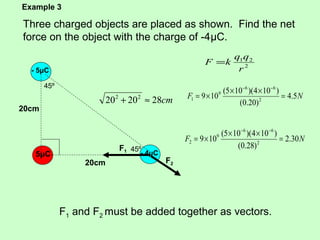
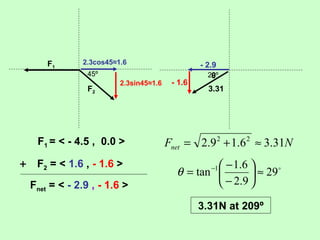
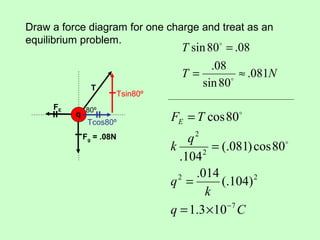
1) The document discusses electric charge and Coulomb's law. It defines fundamental charge, positive and negative charge, and conservation of charge. 2) Coulomb's law gives the electric force between two point charges, and states that the force is proportional to the product of the charges and inversely proportional to the square of the distance between them. 3) Examples are given to calculate electric force between charges and compare it to gravitational force. The net force on a charge from multiple other charges is also demonstrated.

1. Electric Charge
and
Coulomb’s Law

2. Fundamental Charge: The charge
on one electron.
e = 1.6 x 10 -19
C
Unit of charge is a Coulomb (C)

3. Two types of charge:
Positive Charge: A shortage of electrons.
Negative Charge: An excess of electrons.
Conservation of charge – The net charge of a
closed system remains constant.

4. +
n
+ +
+
+
+
n
n
n
n n
-
-
-
-
-
-
Neutral Atom
Number of electrons = Number of protons
Nucleus
Negative Atom
Number of electrons > Number of protons
-2e = -3.2 x 10-19
C
-
-
Positive Atom
Number of electrons < Number of protons
+2e = +3.2 x 10-19
C

5. Electric Forces
Like Charges - Repel
Unlike Charges - Attract
- +F F
+ +
FF

6. Coulomb’s Law – Gives the electric force
between two point charges.
2
21
r
qq
kF =
k = Coulomb’s Constant = 9.0x109
Nm2
/C2
q1 = charge on mass 1
q2 = charge on mass 2
r = the distance between the two charges
The electric force is much stronger than the
gravitational force.
Inverse Square
Law

7. 2
21
r
qq
kF =
If r is doubled then F is :
If q1 is doubled then F is :
If q1 and q2 are doubled and r is halved then F is :
¼ of F
2F
16F
Two charges are separated by a distance r and have a force
F on each other.
q1
q2
r
F F
Example 1

8. Example 2
Two 40 gram masses each with a charge of 3μC are
placed 50cm apart. Compare the gravitational force
between the two masses to the electric force between the
two masses. (Ignore the force of the earth on the two
masses)
3μC
40g
50cm
3μC
40g

9. 2
21
r
mm
GFg =
2
11
)5.0(
)04)(.04(.
1067.6 −
×= N13
1027.4 −
×≈
2
21
r
qq
kFE =
2
66
9
)5.0(
)103)(103(
100.9
−−
××
×= N324.0≈
The electric force is much greater than the
gravitational force

10. 5μC
- 5μC
Three charged objects are placed as shown. Find the net
force on the object with the charge of -4μC.
- 4μC
F2
F1
F1 and F2 must be added together as vectors.
20cm
20cm
cm282020 22
≈+
45º
45º
2
21
r
qq
kF =
NF 5.4
)20.0(
)104)(105(
109 2
66
9
1 =
××
×=
−−
NF 30.2
)28.0(
)104)(105(
109 2
66
9
2 =
××
×=
−−
Example 3

11. F1
F2
45º
2.3cos45≈1.6
2.3sin45≈1.6
F1 = < - 4.5 , 0.0 >
F2 = < 1.6 , - 1.6 >+
Fnet = < - 2.9 , - 1.6 >
NFnet 31.36.19.2 22
≈+=
- 2.9
- 1.6
3.31
θ

29
9.2
6.1
tan 1
≈





−
−
= −
θ
3.31N at 209º
29º

12. Example 4
Two 8 gram, equally charged balls are suspended on earth
as shown in the diagram below. Find the charge on each
ball.
qq
20º
L = 30cmL = 30cm
FEFE
r =2(30sin10º)=10.4cm
2
2
2
21
r
q
k
r
qq
kFE ==
10º10º
30sin10º
r

13. Draw a force diagram for one charge and treat as an
equilibrium problem.
FE
Fg = .08N
T
q
Tsin80º
NT
T
081.
80sin
08.
08.80sin
≈=
=


Tcos80º
Cq
k
q
q
k
TFE
7
22
2
2
103.1
)104(.
014.
80cos)081(.
104.
80cos
−
×=
=
=
=

80º