1. This document discusses changing the order of integration when evaluating double integrals over rectangles. To evaluate a double integral, we first integrate with respect to one variable while treating the other as a constant, and then integrate with respect to the remaining variable. 2. It provides definitions and properties of double integrals, including that a double integral over a rectangle exists if the integrand function is integrable over the region. 3. Examples are given to illustrate continuous and non-continuous integrand functions over different regions.

1. Government engineering
college.
CALCULUS (2110014)
TOPIC: MULTIPLE INTEGRALS : CHANGE THE ORDER OF INEGRATION
1

2. Change of Order of Integration
 To evaluating a double integral we integratefirst with respect
to one variable andconsidering the other variable as
constant,and then integrate with respect to theremaining
variable. In the former case, limitsof integration are
determined in the givenregion by drawing stripes parallel to y-
axiswhile in second case by drawing strips parallel to x-axis.
2

3. Double Integrals over Rectangles
Remark:-
)取樣點(point.sample
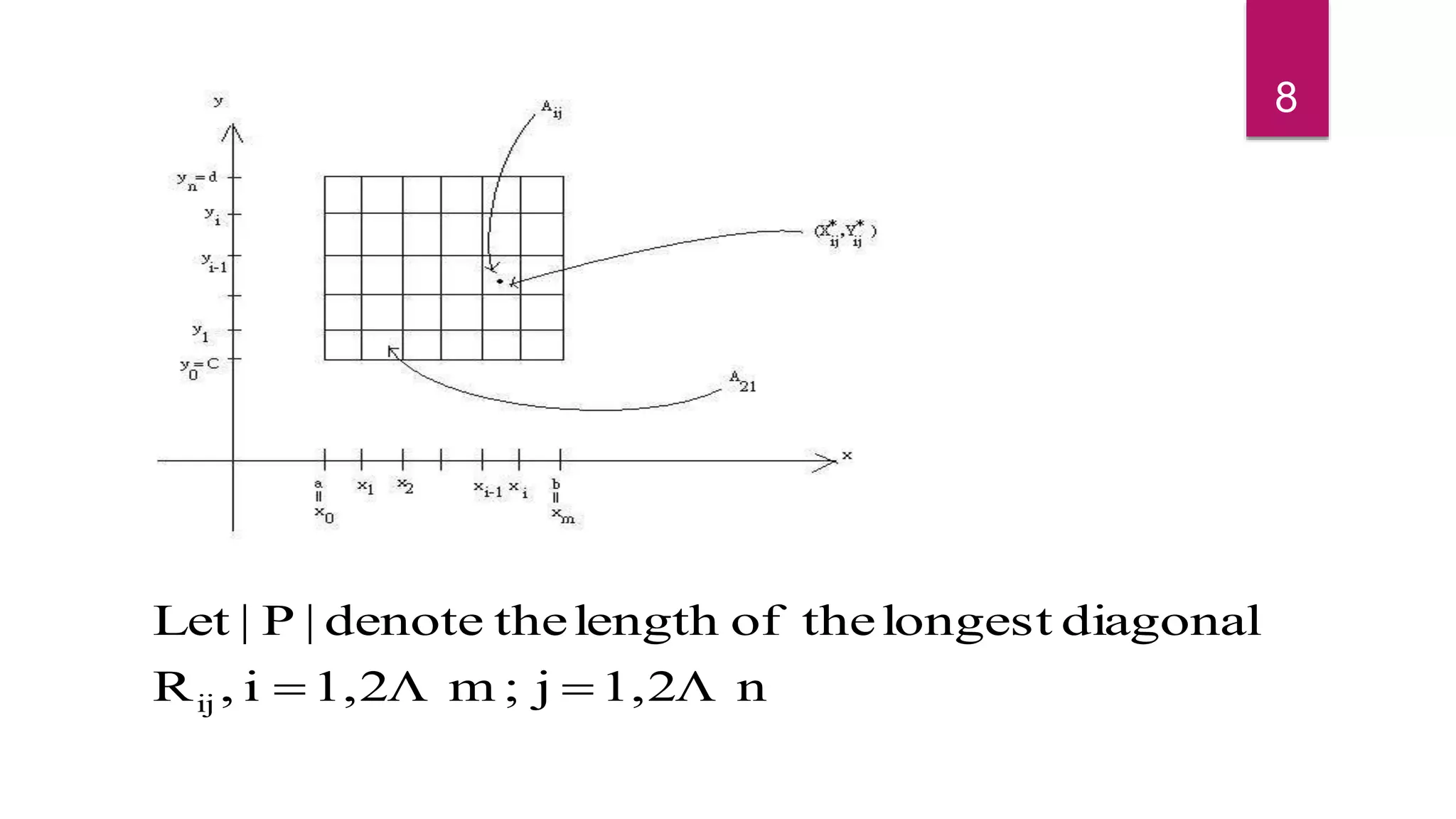
acalledisx1,2,...n,i],x,[xxChoose4.
Pofnorm}Thex,,x,xmax{|P|3.
n,1,2,i,x-xxDefine2.
b],[aofpartitionacalledisPThen
bxxxaand}x,,x,{xPLet1.
ii1-ii
n21
1-iii
n10n10







3

4.  


n
1i
ii
b
a 0P||
SofareaThex)xf(limf(x)dx
b],[aonfofintegraldefiniteThe5.
f(x)}y0b,xa|y){(x,S 
4

5. [2,3][1,2]2.
4}y21,x0|Ry){(x,[2,4][0,1]1.
Rectangle:Example
d}ycb,xa|Ry){(x,d][c,b][a,R
RrectangleclosedA6.
2
2



5

6. V(S)-SofvolumethefindTo
y)}f(x,zR,0y)(x,|Rz)y,{(x,Sd],[c,b][a,RLet 3

lssubintervaintoRrectangletheDivide
f(x)dxdefinetoSimilarly
b
a
6

7. 

 
 






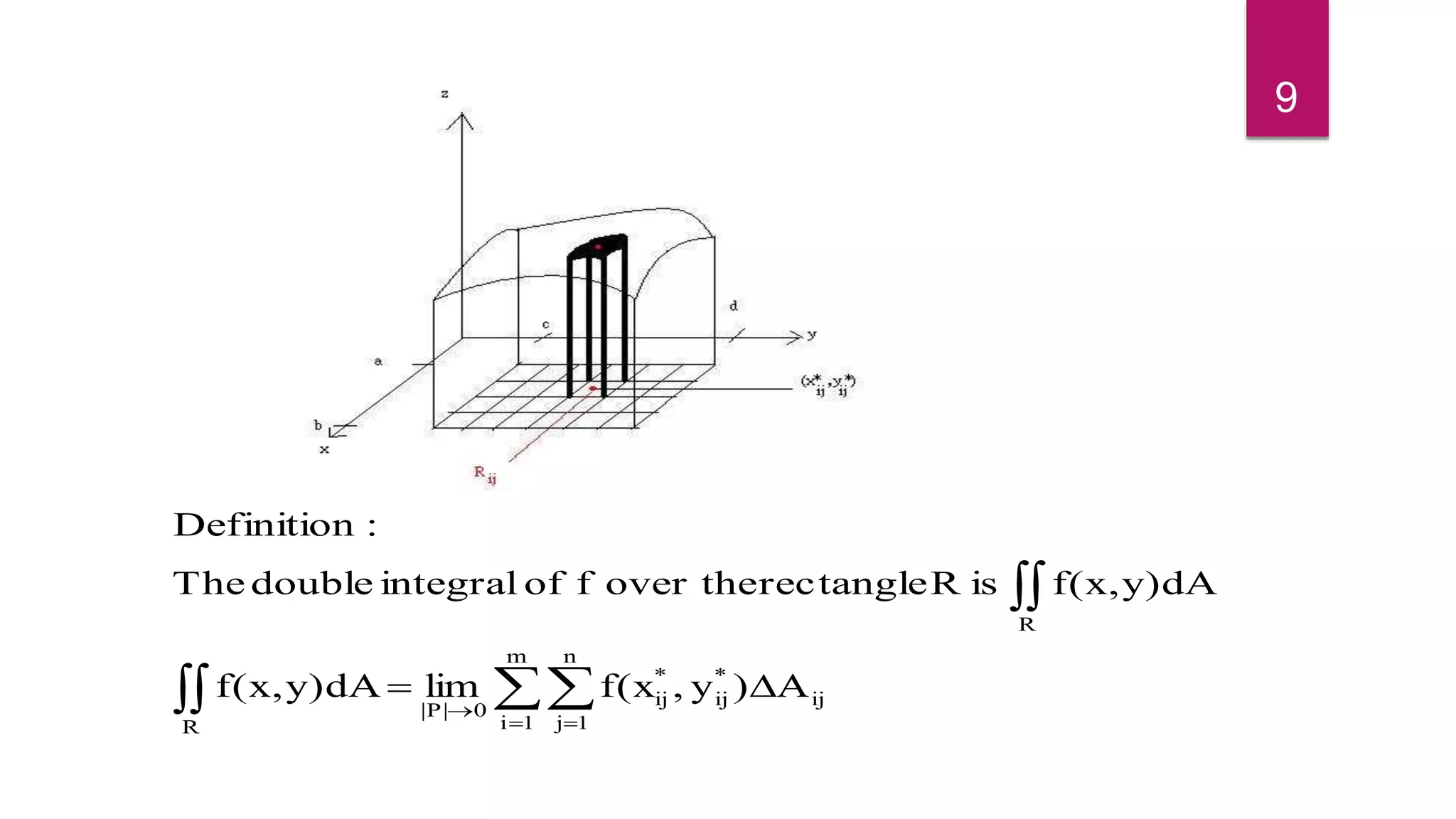
n
1j
m
1i
ij
*
ij
*
ij
n
1j
m
1i
ij
*
ij
*
ij
ij
*
ij
*
ij
jiijij
j1-ji1-iij
1-jjjj1-j
1-iii
i1-i
A)y,f(xV(S)i.e
A)y,f(xeapproximatcanSofvolumeThe
Reachin)y,(xpointsampleachoose
yxAisRofareaThe
n1,j;m1,i]y,[y]x,[xRDefine
n1,2,j,y-yy],y,[ylsubintervaninto
dividedisd][c,and,x-xxm,1,2,i
]x,[xlsubintervamintodividedisb][a,



7

8. n1,2j;m1,2i,R
diagonallongesttheoflengththedenote|P|Let
ij  
8

9. 

 


m
1i
n
1j
ij
*
ij
*
ij
0P||
R
R
A)y,f(xlimy)dAf(x,
y)dAf(x,isRrectangleover thefofintegraldoubleThe
:Definition
9

10.  
  
 




R R
R R R
R R
y)dAg(x,y)dAf(x,
thenR,y)(x,y)g(x,y)f(x,If3.
y)dAg(x,y)dAf(x,y))dAg(x,y)(f(x,2.
y)dAf(x,cy)dAcf(x,1.
:properties
existslimitthisif
10

11. Ronintegrableisfthencurves,smooth
ofnumberfiniteaonexceptRoncontinuousisfIf(ii)
RonintegrableisfthenR,oncontinuousisfIf(i)
Rrectabgleclosedon theboundedbefLet
1Theorem
Roverfofintegraldoublethecalledisy)dAf(x,2.
existA)y,f(xlimifR,onintegrableisf1.
:Definition
R
m
1i
n
1j
ij
*
ij
*
ij
0P||

 


11

12. ww),(o,oncontinuousnotisf
(0,1)oncontinuousnotisf
0x0,
0x,
x
y
y)f(x,3.
Roncontinuousisf
)[0,)[0,Rx,yxy)f(x,2.
Roncontinuousisf
][0,2][0,Ry)(x,sinxy,y)f(x,1.
:Example
RoncontinuousisfthenR,b)(a,allatcontinuousisfIf2.
b)(a,atcontinuousisfthenb),f(a,y)f(x,limIf1.
:Definition
2
b)(a,y )(x,














12

13. -Thank you.
13