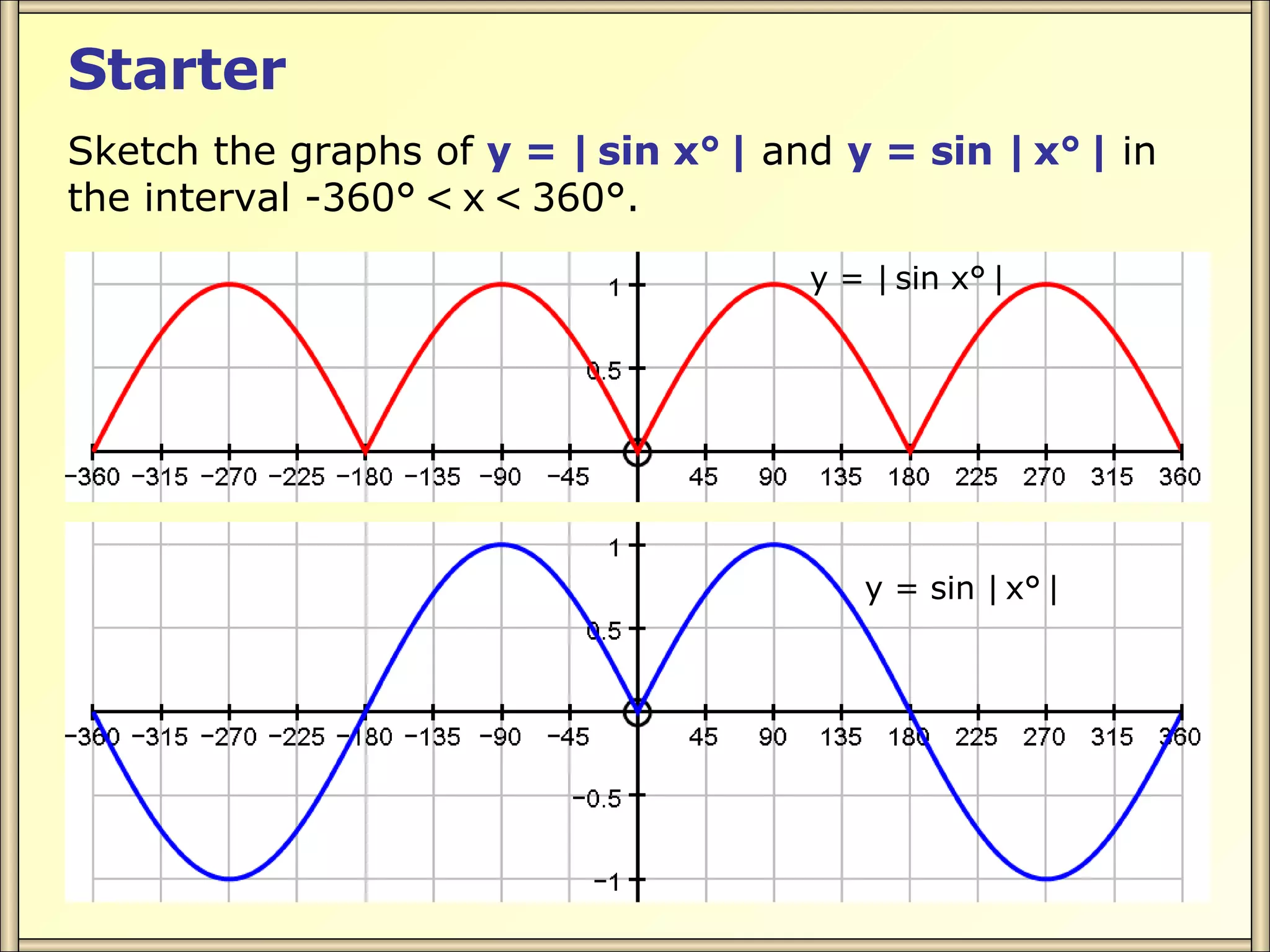
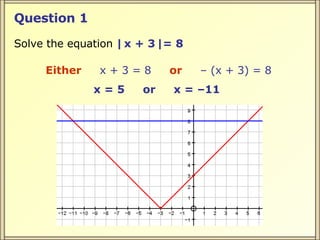
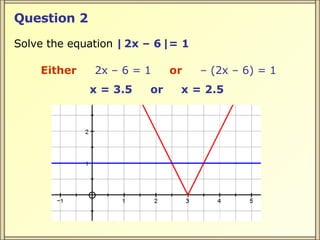
The document discusses solving simple modulus equations by setting the expressions equal and solving, either by isolating the variable or squaring both sides. It provides examples of solving equations of the form |ax + b| = c and |ax + b| = |cx + d|. The examples show setting the expressions equal, isolating the variable, and finding the solutions, or squaring both sides to remove the modulus and then solving the resulting equation.

1. Starter Sketch the graphs of y = | sin x° | and y = sin | x° | in the interval -360° < x < 360°. y = | sin x° | y = sin | x° |

2. The modulus is defined as follows: Objective: to solve simple modulus equations

3. Question 1 Solve the equation | x + 3 |= 8 Either x + 3 = 8 or – (x + 3) = 8 x = 5 or x = –11

4. Question 2 Solve the equation | 2x – 6 |= 1 Either 2x – 6 = 1 or – (2x – 6) = 1 x = 3.5 or x = 2.5

5. Question 3 Solve the equation | x – 2 | = | 2x – 1 | The technique this time is to square both sides of the equation. WARNING: this only works if there is a modulus on both sides of the equation. (x – 2)² = (2x – 1)² x² – 4x + 4 = 4x² – 4x + 1 x² = 1 x = 1 or x = – 1

6. Core 3 & 4 Textbook Exercise 7C Page 127 Question 1

7. Plenary Pure 2 June 2003 Question 1 (3 marks) Find the exact solutions of the equation | 7x – 3 | = | 7x + 6 |. Core 3 June 2005 Question 2 (4 marks) Find the exact solutions of the equation | 6x – 1 | = | x – 1 |.