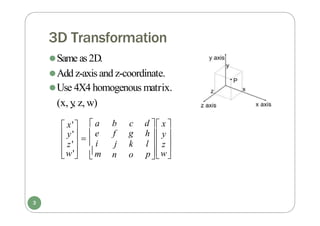
Chapter 5 discusses three-dimensional geometric transformations in computer graphics, covering key components such as 3D translation, rotation, scaling, and coordinate system transformations. It details various transformation methods using 4x4 homogeneous matrices and demonstrates the application of transformations through OpenGL functions. The chapter emphasizes matrix operations and their order in achieving desired transformations in a 3D space.

1. Chapter 5
Three-Dimensional Geometric
Transformations
Computer Graphics
C. P. Divate

2. Outline
⚫ 3DTranslation
⚫ 3D Rotation
⚫ 3D Scaling
⚫ Transformations between 3D Coordinate Systems
⚫ OpenGLGeometricTransformation Functions
⚫ OpenGL3D GeometricTransformation Programming Examples
2

3. 3D Transformation
⚫Same as2D.
⚫Add z-axis and z-coordinate.
⚫Use 4X4 homogenous matrix.
(x, y
, z, w)
p

w

m
l  z 
 i
d  x 
h  y 
 a b c
f g
j k
n o

w'

 z'
 y'   e
 x'
3

4. Right-hand coordinate system
⚫ OpenGL: right-hand
⚫ The positive x and yaxes point right and up, and the zaxispoints to the viewer.
⚫ Positive rotation is counterclockwise about the axis of rotation when looking
alongthe positive halfof the axis toward the origin.
4

5. 3D Translation
⚫ Aposition P=(x,y,z) in 3D space is translated to alocation
P’=(x’,y’,z’) byadding translation distances tx,ty, and tz:
z' z  tz
x' x  tx y' y  ty
FIGURE9-2 Shifting the
position of athree-dimensional
object using translationvectorT
.
  

  

1 
 1 
0 1
0 0 0
0
0 1 0
1 0 0
t  y
z'
 
y'
x'
tz
 z 
y   
tx  x
(9-1)
(9-2)
P' = TP (9-3)
Bymatrix form:
1 
or
5

6. 3D Rotation
Positive rotations:counterclockwise when lookingalongthe positive
half of the axis toward the origin
⚫ Coordinate-AxesRotations
⚫ X-axis,Y
-axisor Z-axis rotation
⚫ Rotation about an axis that is in parallel to one of the coordinate axes
⚫ General 3D Rotations
⚫ Rotation about an arbitraryaxis
6

7. 3D Coordinate Axis Rotation
⚫Rotation of an object about the yaxis
z' = z
⚫Rotation of an object about the zaxis
x' = x cos - ysin
y' = x sin + ycos
 
  
1 1 
 0
1 
⚫ Rotation of an object about the x axis
0 z 
  
0  y
0  x
z'  0
  
y'
Rx  
sin
x' cos sin 0
cos 0
0 1
0 0
 
  
1  1 
 0
1 
0  z 
  
0  y
0  x
y' 0
Ry  
z' sin
  
x' cos 0 sin
1 0
0 cos
0 0




 
  
 

  
  
 
1
 
1

1
1  0
0  z
0  y
0  x
 z' 0

y' 
0
 x' 0 0
  cos sin 
Rz 

    
 
sin cos
0 0
7
z x; x  y; y z.
x  y; y z;z x.

8. 3D Rotations Parallel to Axes
⚫ Rotation an axis that is parallel to one of the coordinate axes
⚫ Translatethe object so that the rotation axis coincides with the parallel
coordinate axis
⚫ Performthe specified rotation about that axis
⚫ Translatethe object so that the rotation axisis moved back to its original
position
8

9. 3D Rotations about Arbitrary Axis
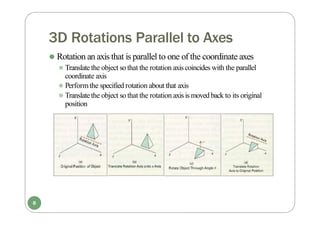
⚫Rotate about the arbitraryaxis through P1 and P2:
1. Translate P1 to origin.
2.Rotate so that the rotation axis is alignedwith one of the
principle coordinate axes.
3. Perform the desired rotation about coordinate axis.
4. Rotate axis back (inverse rotation of 2).
5. Translate axis back(inverse translation of 1).
P1
x
y
z
Arbitraryaxis
P2
9
[T]
[R1]
[R-axis]
[R1]-1
[T]-1

10. 3D Scaling
⚫Scaleobjects relative to the coordinate origin (0, 0, 0)
⚫All vectorsare scaledfrom the origin
Original scale all axes scale Y axis
offset from origin distance from origin also scales
10

11. 3D Scaling
0
      P' SP
0 y
0 x

z
 
 0
y  s y   0 s
x
 
sz 

z

y
sx 0

sz z

y
sx x
or in 3D homogeneous coordinates
 
      
     11
 1   1   0
 
0z
0y
0x
y s y  0
0 0
s 0
0 sz
0 0
y
z sz z  0
y
x sx x sx
(9-41)
11

12. 3D Scaling
⚫Scaling objects relative to aselected fixed point (xf, yf, zf)
Translate fixed point to origin Scale Translate fixed point back
12

13. 3D Scaling
⚫Scaling objects relative to aselected fixed point (xf, yf, zf)
(cont.)

0 z f


y f 
y
f f f x y z f f f

0 sz (1 s )z
0 0 0 1
s 0 (1 s )y

sx 0 0 (1 sx )xf 

0
T(x , y , z )  S(s ,s ,s ) T(x ,y ,z )  


1
00
01
1  0
1
0
f

f 
z
y
f

f 
f f f x y z f f f
xf 
0 0 0 0 0 0
1 0 s 0  1 0  y 
0 0 1 z  0 0 s 00 0 1  z 
0 0 0 0 0 10 0 0

y  0
xf sx
T(x , y , z )S(s ,s ,s )T(x ,y ,z )  
13

14. Matrix Composition
⚫ Transformations can be combined bymatrix multiplication


  
  


 
 
 

1 w
0  z 
0  y 
0 0 0  x 
sy 0
0 sz
0 0
0 0
0sx
1 
 0

w'
  0
 z' 
 0
 y'
 x'
p’ = T(tx,ty)
 1 0 0 tx cos   sin  0
1 0 ty sin  cos  0
 
0 1 tz  0 0 1 0 0
0 0 0 0 0 1 0
R(Q) S(sx,sy) p
p’= (T * (R * (S*p) ) )
p’= (T*R*S ) * p
⚫ Order of transformations
⚫Matrix multiplication is not commutative
p’= T * R* S* p
“Global” “Local”
14

15. Transformations Between 3D Coordinate Systems
Mxyz, x'y'z' = R˙T(-x0, -y0, -z0)
 If different scalesare used in the two coordinate systems, the scalingtransformation
mayalso be needed.


(P313) 0 
0 
0
y1 y2 y3
u'z1 u'z2 u'z3

0 0 1
u' u' u'
u'x1 u'x2 u'x3 0
R  
FIGURE9-21 Anew x’y’z’coordinate system
defined within an xyzsystem.Ascene description
istransferred to the new coordinate reference
usinga transformationsequencethat
superimposes the x’y’z’frame on the xyzaxes.
 Totransfer the xyz coordinate descriptions -> x’y’z’coordinate system
 Translation: bring the x’y’z’coordinate origin to the position of the xyz origin.
 Transform x’y’z’ onto the corresponding axes xyz: the coordinate-axis rotation
matrix formed bythe unit axisvectors.
which transforms unit vector u’x,
u’y,u’z onto the x,yand z axes.
15

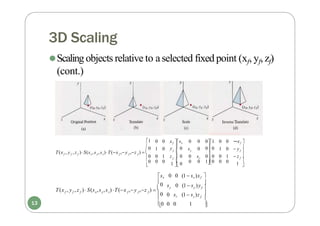
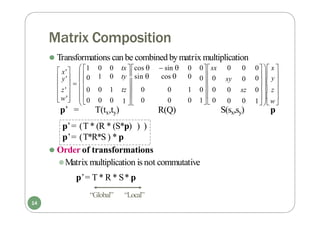
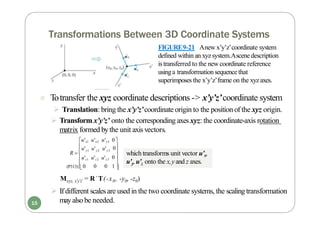
16. OpenGL Geometric Transformation Functions
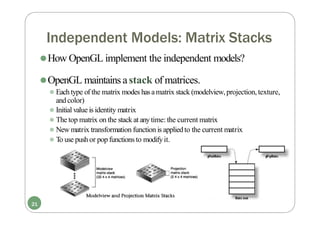
⚫Becareful of manipulating the matrix in OpenGL
⚫OpenGLuses 4X4 matrix for transformation.
⚫The 16 elements are stored as1D in column-majororder
OpenGLtransformmatrix
⚫C and C++ store matrices in row-majororder
⚫Ifyou declare amatrix to be used in OpenGLas
GLfloat M[4][4];to accessthe element in row i and column j, you
need to refer to it byM[j][i];or, as
GLfloat M[16];and then you need to convert it to conventional row-
majororder.
16

17. OpenGL Transformations
⚫All the transformations done byOpenGLcan be
described asamultiplication of two or more
matrices.
⚫The mathematicsbehind these transformations are greatly
simplifiedbythe mathematicalnotation of the matrix.
⚫Eachof the transformations can be achieved bymultiplying a
matrix that contains the vertices,bya matrix that describes
the transformation.
17

18. OpenGL Geometric Transformation Functions
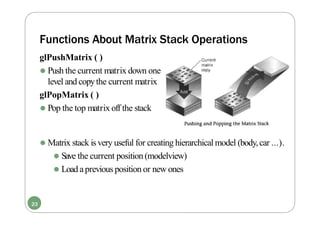
⚫ BasicOpenGLgeometrictransformations on the matrix:
glT
ranslate* (tx, ty
, tz);
[ glTranslatef(25.0,-10.0,10.0);
- Post-multiplies the current matrix byamatrix that moves the object bythe given x-,
y-, and z-values
glScale* (sx, sy
, sz);
[glScalef (2.0, -3.0, 1.0); ]
- Post-multiplies the current matrix byamatrix that scalesan object about the origin.
None of sx, syor sziszero.
glRotate* (theta,vx, vy
, vz);
[ glRotatef (90.0, 0.0, 0.0, 1.0); ]
- Post-multiplies the current matrix byamatrix that rotates the object in a
counterclockwise direction. vector v=(vx, vy,vz) defines the orientation for the
rotation axis that passesthrough the coordinate origin.( the rotation center is (0, 0, 0) )
18

19. OpenGL: Order in Matrix Multiplication
glMatrixMode (GL_MODELVIEW);
glLoadIdentity ( ); //Set current matrix to the identity
.
glMultMatrixf (elemsM2);//P ost-multiplyidentity bymatrix M2.
glMultMatrixf (elemsM1);//P ost-multiplyM2bymatrix M1.
glBegin (GL_POINTS)
glV
ertex3f (vertex);
glEnd( );
Modelview matrix successivelycontains:
I(identity),M2, M2 M1
The concatenated matrix is:
M=M2 M1
The transformed vertex is:
M2(M1 vertex)
In OpenGL, atransformation sequence is applied in reverse
order of which it isspecified.
19

20. OpenGL: Order in Matrix Multiplication
⚫Example
/ / rotate object 30 degrees around X-axis
glRotatef(30.0, 1.0, 0.0, 0.0);
/ / move object to (x, y
, z)
glTranslatef(x, y
, z);
drawObject();
The object will be translated first then rotated.
20

21. Independent Models: Matrix Stacks
⚫How OpenGL implement the independent models?
⚫OpenGL maintains astack of matrices.
⚫ Each type of the matrix modes hasamatrix stack (modelview,projection,texture,
and color)
⚫ Initial value is identity matrix
⚫ The top matrix on the stack at anytime: the current matrix
⚫ New matrix transformation function is appliedto the current matrix
⚫ To use push or pop functions to modifyit.
21

22. Functions About Matrix Stack Operations
⚫ Find the maximum allowablenumber of matrices in stack
glGetIntegerv (GL_MAX_MODELVIEW_STACK_DEPTH,
stackSize);
glGetIntegerv (GL_MAX_PROJECTION_STACK_DEPTH,
stackSize);
⚫ Find out how manymatrices are currentlyin the stack
glGetIntegerv (GL_MODEL
VIEW_ST
ACK_DEPTH, numMats);
22

23. Functions About Matrix Stack Operations
glPushMatrix ( )
⚫ Push the current matrix down one
level and copythe current matrix
glPopMatrix ( )
⚫ Pop the top matrix off the stack
⚫ Matrix stack is very useful for creating hierarchical model (body,car ...).
⚫ Save the current position (modelview)
⚫ Load aprevious position or new ones
23

24. Matrix Stack Operations
⚫Example
glMatrixMode(GL_MODEL
VIEW);
glPushMatrix ();
glTranslatef( 0.0, 0.0, -8.0 );
glTranslatef( 1.0, 0.0, 0.0 );
DrawObj ();
glPopMatrix ();
modelview matrix stack
24

25. OpenGL Geometric Trans. Programming Examples
glMatrixMode (GL_MODEL
VIEW); //Identity matrix
glColor3f (0.0, 0.0, 1.0);
glRecti (50, 100, 200, 150);
/ / Set current color to blue
/ / Displayblue rectangle.
glColor3f (1.0, 0.0, 0.0); / / Red
glTranslatef (-200.0, -50.0, 0.0); / / Set translation parameters.
glRecti (50, 100, 200, 150); / / Displayred, translated rectangle.
glLoadIdentity (); / / Reset current matrix to identity
.
glRotatef (90.0, 0.0, 0.0, 1.0); / / Set 90-deg, rotation about zaxis.
glRecti (50, 100, 200, 150); / / Displayred, rotated rectangle.
glLoadIdentity ();
glScalef (-0.5, 1.0, 1.0);
/ / Reset current matrix to identity
.
/ / Set scale-reflection parameters.
glRecti (50, 100, 200, 150); / / Displayred, transformed rectangle.
25

26. OpenGL Geometric Trans. Programming Examples
glColor3f (0.0, 0.0, 1.0);
glRecti (50, 100, 200, 150);
/ / Set current color to blue.
/ / Displayblue rectangle.
glPushMatrix (); / / Make copyof identity (top) matrix.
glColor3f (1.0, 0.0, 0.0); / / Set current color to red.
glTranslatef (-200.0, -50.0, 0.0); / / Set translation parameters.
glRecti (50, 100, 200, 150); / / Displayred, translated rectangle.
glPopMatrix (); / / Throw awaythe translation matrix.
glPushMatrix (); / / Make copyof identity (top) matrix.
glRotatef (90.0, 0.0, 0.0, 1.0); / / Set 90-deg, rotation about zaxis.
glRecti (50, 100, 200, 150); / / Displayred, rotated rectangle.
glPopMatrix (); / / Throw awaythe rotation matrix.
glScalef (-0.5, 1.0, 1.0);
glRecti (50, 100, 200, 150);
/ / Set scale-reflection parameters.
/ / Displayred, transformed rectangle.
⚫More efficient way:glPushMatrix/glPopMatrix
glMatrixMode (GL_MODEL
VIEW);
26

27. Example
⚫Drawing acar’wheels with bolts
draw_wheel( );
for (j=0; j<5; j++) {
glPushMatrix ();
glRotatef(72.0*j, 0.0, 0.0, 1.0);
glTranslatef (3.0, 0.0, 0.0);
draw_bolt ( );
glPopMatrix ( );
}
R
RT
RTv
Global – Bottom Up
Start Rot
Trans
The wheels and bolt axes are coincident with z-axis;the
bolts are evenlyspaced every72 degrees,3 units fromthe
center of the wheel.
27

28. Summary
⚫ Basic3D geometrictransformations
⚫ Translation
⚫ Rotation
⚫ Scaling
⚫ Combination of these transformations
⚫ OpenGL3D geometric transformation functions
⚫ GL_MODEL
VIEWmatrix
⚫ Order in multiple matrix multiplication
⚫ Matrix stack
⚫ glPushMatrix ()
⚫ glPopMatrix ()
28