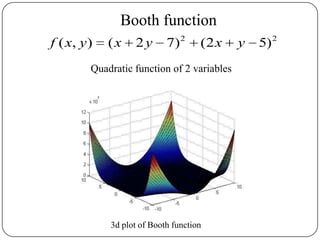
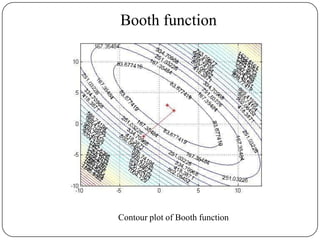
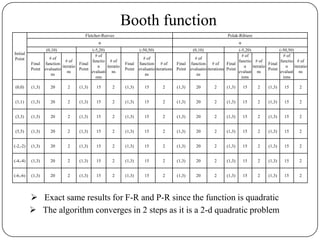
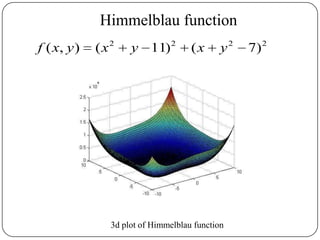
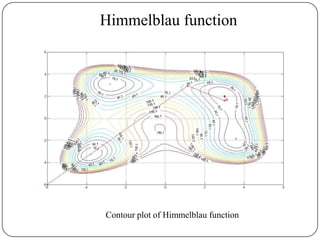
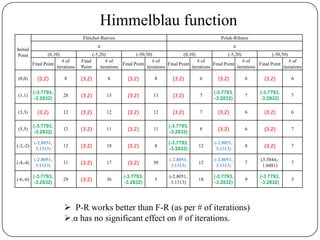
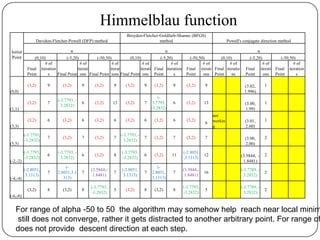
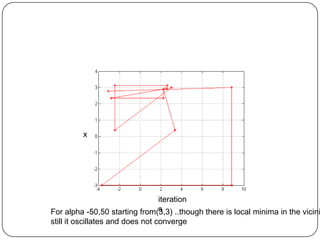
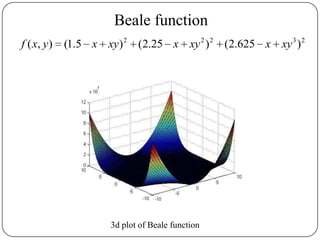
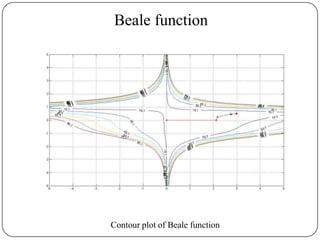
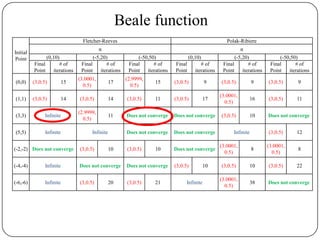
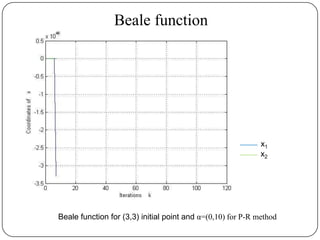
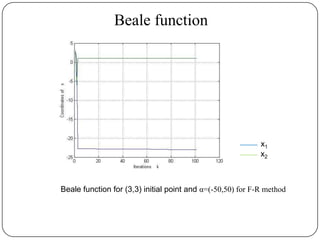
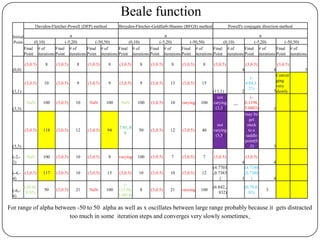
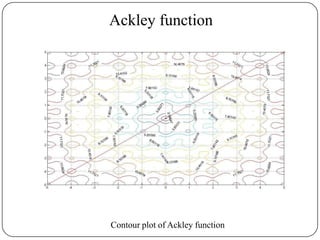
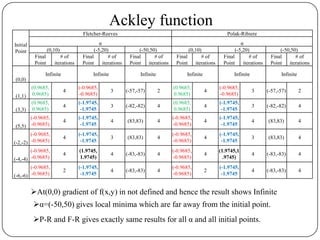
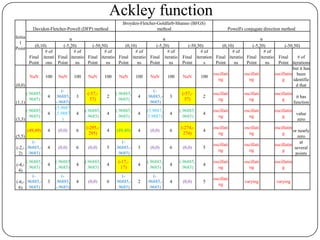
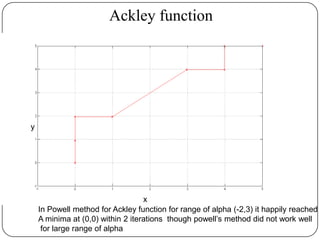
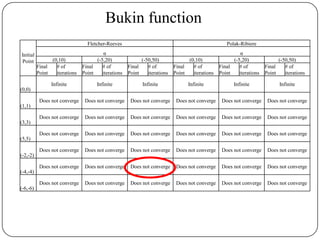
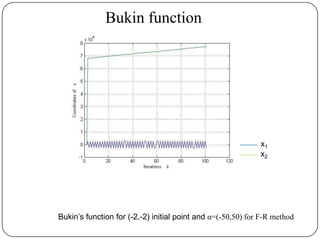
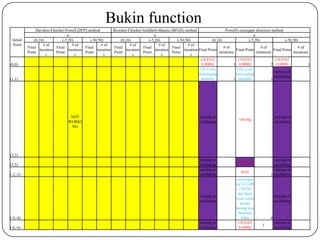
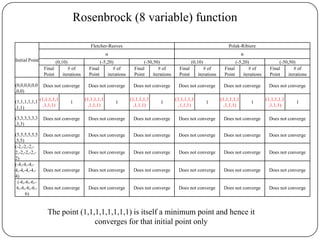
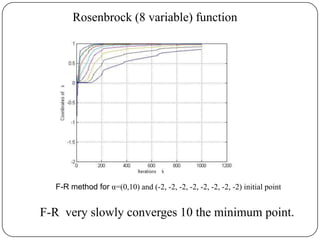
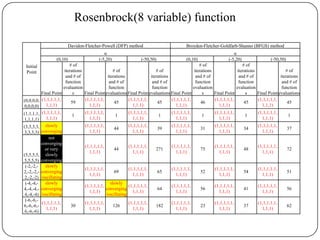
The document presents a comparative study of algorithms for nonlinear optimization. It evaluates several nonlinear optimization algorithms (conjugate gradient methods, quasi-Newton methods, Powell's method) on standard test functions (Booth, Himmelblau, Beale) from different initial points and step sizes. For the Booth function, all algorithms converge in 2 steps. For Himmelblau, Polak-Ribiere and BFGS methods perform best. For Beale, conjugate gradient methods converge for some initial points but not all, while Powell's method converges from more points.

1. Presented by
Pritam Bhadra
Pranamesh Chakraborty
Indian Institute of Technology, Kanpur
11 May 2013
Comparative study of algorithms of
Nonlinear Optimization

2. Methods of Nonlinear Optimization
The methods for nonlinear optimization are:
1. Conjugate gradient methods
a) Fletcher-Reeves
b) Polak- Ribiere
2. Powell’s conjugate direction method
3. Quasi-Newton methods
a) Davidon-Fletcher-Powell (DFP) method
b) Broyden-Fletcher-Goldfarb-Shanno (BFGS) method

3. Functions used for comparison of algorithms
1. Booth function
2. Himmelblau function
3. Beale function
4. Ackley function
5. Goldstein function
6. Cross-in-tray function
7. Bukin function
8. Rosenbrock function

4. For each function(two-dimensional), local minima is obtained
from 6 initial points:
a) (0,0)
b) (1,1)
c) (3,3)
d) (5,5)
e) (-2,-2)
f) (-4,-4)
g) (-6,-6)
for 3 ranges of α (step-size)
 (0,10)
 (-5,20)
 (-50,50)

5. Booth function
2 2
( , ) ( 2 7) (2 5)f x y x y x y
Quadratic function of 2 variables
3d plot of Booth function

6. Booth function
Contour plot of Booth function

7. Booth function
 Exact same results for F-R and P-R since the function is quadratic
Initial
Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
function
evaluatio
ns
# of
iteratio
ns
Final
Point
# of
functio
n
evaluati
ons
# of
iteratio
ns
Final
Point
# of
function
evaluatio
ns
# of
iterations
Final
Point
# of
function
evaluatio
ns
# of
iterations
Final
Point
# of
functio
n
evaluat
ions
# of
iteratio
ns
Final
Point
# of
functio
n
evaluat
ions
# of
iteratio
ns
(0,0) (1,3) 20 2 (1,3) 15 2 (1,3) 15 2 (1,3) 20 2 (1,3) 15 2 (1,3) 15 2
(1,1) (1,3) 20 2 (1,3) 15 2 (1,3) 15 2 (1,3) 20 2 (1,3) 15 2 (1,3) 15 2
(3,3) (1,3) 20 2 (1,3) 15 2 (1,3) 15 2 (1,3) 20 2 (1,3) 15 2 (1,3) 15 2
(5,5) (1,3) 20 2 (1,3) 15 2 (1,3) 15 2 (1,3) 20 2 (1,3) 15 2 (1,3) 15 2
(-2,-2) (1,3) 20 2 (1,3) 15 2 (1,3) 15 2 (1,3) 20 2 (1,3) 15 2 (1,3) 15 2
(-4,-4) (1,3) 20 2 (1,3) 15 2 (1,3) 15 2 (1,3) 20 2 (1,3) 15 2 (1,3) 15 2
(-6,-6) (1,3) 20 2 (1,3) 15 2 (1,3) 15 2 (1,3) 20 2 (1,3) 15 2 (1,3) 15 2
 The algorithm converges in 2 steps as it is a 2-d quadratic problem

8. Booth function
Init
ial
Poi
nt
Davidon-Fletcher-Powell (DFP)
method
Broyden-Fletcher-Goldfarb-Shanno
(BFGS) method Powell's conjugate direction method
α α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
Final
Point
# of
iterati
ons
(0,0
)
(1,3) 2,36 (1,3) 2,29 (1,3) 2,23 (1,3) 2,40 (1,3) 2,31 (1,3) 2,26
(3.4,1.
08)
(1,3) 1 (1,3) 1
(1,1
)
(1,3) 2,43 (1,3) 2,29 (1,3) 2,38 (1,3) 2,42 (1,3) 2,28 (1,3) 2,32
(2.6,1.
72)
(1,3) 1 (1,3) 1
(3,3
)
(1,3) 2,35 (1,3) 2,29 (1,3) 2,32 (1,3) 2,44 (1,3) 2,29 (1,3) 2,31 (1,3) 1 (1,3) 1
(5,5
)
(1,3) 2,32 (1,3) 2,27 (1,3) 2,22 (1,3) 2,37 (1,3) 2,28 (1,3) 2,24
Not
Worki
ng
reachi
ng to
an
(1,3) 2 (1,3) 2
(-
2,-
2)
(1,3) 2,44 (1,3) 2,28 (1,3) 2,39 (1,3) 2,35 (1,3) 2,28 (1,3) 2,31
arbitr
ary
point
and
oscill
ates
(1,3) 1 (1,3) 1
(-
4,-
4)
(1,3) 2,36 (1,3) 2,27 (1,3) 2,26 (1,3) 2,38 (1,3) 2,26 (1,3) 2,27
aroun
d the
point.
(1,3) 1 (1,3) 1
(-
6,-
6)
(1,3) (2,38) (1,3) 2,31 (1,3) 2,36 (1,3) 2,36 (1,3) 2,25 (1,3) 2,31 (1,3) 1 (1,3) 1
DFP and BFGS works very well for Booth functionPowell’s method works nice for proper range of
alpha. A bit large range of alpha can be taken as
there is only a few local minima of the function.
For range of alpha between 0 and 10 it did not work
because in some steps for ensuring the step to be
descent the value of alpha is coming out to be
negative.

9. Himmelblau function
2 2 2 2
( , ) ( 11) ( 7)f x y x y x y
3d plot of Himmelblau function

10. Himmelblau function
Contour plot of Himmelblau function

11. Himmelblau function
Initial
Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final Point
# of
iterations
Final
Point
# of
iterations
Final Point
# of
iterations
Final Point
# of
iterations
Final Point
# of
iterations
Final Point
# of
iterations
(0,0) (3,2) 8 (3,2) 8 (3,2) 8 (3,2) 6 (3,2) 6 (3,2) 6
(1,1)
(-3.7793,
-3.2832)
28 (3,2) 13 (3,2) 13 (3,2) 7
(-3.7793,
-3.2832)
7
(-3.7793,
-3.2832)
7
(3,3) (3,2) 12 (3,2) 12 (3,2) 12 (3,2) 7 (3,2) 6 (3,2) 6
(5,5)
(-3.7793,
-3.2832)
12 (3,2) 11 (3,2) 11
(-3.7793,
-3.2832)
8 (3,2) 6 (3,2) 7
(-2,-2)
(-2.8051,
3.1313)
12 (3,2) 18 (3,2) 8
(-3.7793,
-3.2832)
12
(-2.8051,
3.1313)
8 (3,2) 7
(-4,-4)
(-2.8051,
3.1313)
11 (3,2) 17 (3,2) 50
(-2.8051,
3.1313)
12
(-2.8051,
3.1313)
7
(3.5844,-
1.8481)
7
(-6,-6)
(-3.7793,
-3.2832)
29 (3,2) 36
(-3.7793,
-3.2832)
5
(-2.8051,
3.1313)
18
(-3.7793,
-3.2832)
9
(-3.7793,
-3.2832)
5
 P-R works better than F-R (as per # of iterations)
.α has no significant effect on # of iterations.

12. Himmelblau function
Initial
Point
Davidon-Fletcher-Powell (DFP) method
Broyden-Fletcher-Goldfarb-Shanno (BFGS)
method Powell's conjugate direction method
α α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iteration
s Final Point
# of
iterati
ons Final Point
# of
iterat
ions Final Point
# of
iterati
ons
Final
Point
# of
iteration
s
Final
Point
# of
iterati
ons
Final
Point
# of
iteratio
ns
Final
Point
# of
iterati
ons
Final
Point
# of
iteration
s
(0,0)
(3,2) 9 (3,2) 9 (3,2) 9 (3,2) 9 (3,2) 9 (3,2) 9 (3.02,
1.996)
1
(1,1)
(3,2) 7
(-3.7793, -
3.2832)
6 (3,2) 13 (3,2) 7
(-
3.7793,
-3.2832)
6 (3,2) 13 (3.00,
1.99)
1
(3,3)
(3,2) 6 (3,2) 6 (3,2) 6 (3,2) 6 (3,2) 6 (3,2)
6
not
workin
g
(3.01,
2.00)
1
(5,5)
(-3.7793,
-3.2832)
7 (3,2) 7 (3,2) 7
(-3.7793, -
3.2832)
7 (3,2) 7 (3,2) 7 (3.00,
2.00)
2
(-2,-2)
(-3.7793,
-3.2832)
6
(-3.7793, -
3.2832)
6 (3,2) 8
(-3.7793,
-3.2832)
6 (3,2) 11
(-2.8051
,3.1313)
12 (3.5844, -
1.8481)
2
(-4,-4)
(-2.8051,
3.1313)
7
(-
2.8051,3.1
313)
7
(3.5844,-
1.8481)
7
(-2.8051,
3.1313)
7
(-
2.8051,
3.1313)
7
(3.5844,-
1.8481)
16
(-3.7789, -
3.2832)
2
(-6,-6)
(3,2) 8 (3,2) 8
(-3.7793,
-3.2832)
5 (3,2) 8 (3,2) 8
(-3.7793,
-3.2832)
5
(-3.7789, -
3.2832)
2
For range of alpha -50 to 50 the algorithm may somehow help reach near local minim
still does not converge, rather it gets distracted to another arbitrary point. For range of
does not provide descent direction at each step.

13. For alpha -50,50 starting from(3,3) ..though there is local minima in the vicini
still it oscillates and does not converge
iteration
s
x

14. Beale function
2 2 2 3 2
( , ) (1.5 ) (2.25 ) (2.625 )f x y x xy x xy x xy
3d plot of Beale function

15. Beale function
Contour plot of Beale function

16. Beale function
Initial
Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0) (3,0.5) 15
(3.0001,
0.5)
17
(2.9999,
0.5)
15 (3,0.5) 9 (3,0.5) 9 (3,0.5) 9
(1,1) (3,0.5) 14 (3,0.5) 14 (3,0.5) 11 (3,0.5) 17
(3.0001,
0.5)
16 (3,0.5) 11
(3,3) Infinite
(2.9999,
0.5)
11 Does not converge Does not converge (3,0.5) 10 Does not converge
(5,5) Infinite Infinite Does not converge Does not converge Infinite (3,0.5) 12
(-2,-2) Does not converge (3,0.5) 10 (3,0.5) 10 Does not converge
(3.0001,
0.5)
8
(3.0001,
0.5)
8
(-4,-4) Infinite Does not converge Does not converge (3,0.5) 10 (3,0.5) 10 (3,0.5) 22
(-6,-6) Infinite (3,0.5) 20 (3,0.5) 21 Infinite
(3.0001,
0.5)
38 Does not converge

17. Beale function
x1
x2
Beale function for (3,3) initial point and α=(0,10) for P-R method

18. Beale function
x1
x2
Beale function for (3,3) initial point and α=(-50,50) for F-R method

19. Beale function
Initial
Point
Davidon-Fletcher-Powell (DFP) method Broyden-Fletcher-Goldfarb-Shanno (BFGS) method Powell's conjugate direction method
α α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0)
(3,0.5) 8 (3,0.5) 8 (3,0.5) 8 (3,0.5) 8 (3,0.5) 8 (3,0.5) 8 (3,0.5)
4
(3,0.5)
4
(3,0.5)
3
(1,1)
(3,0.5) 10 (3,0.5) 9 (3,0.5) 9 (3,0.5) 9 (3,0.5) 13 (3,0.5) 15
(11,1) 2
(-
4.04,1.
21)
7
Conver
ging
very
slowly
(3,3)
NaN 100 (3,0.5) 10 NaN 100 NaN 100 (3,0.5) 10 varying 100
not
varying
(3,3)
__
(-
0.1198,
3.0003) 3
(5,5)
(3,0.5) 118 (3,0.5) 12 (3,0.5) 94
7.93,.8
6
50 (3,0.5) 12 (3,0.5) 40
not
varying
(5,5)
may be
get
stuck
to a
saddle
point(0
,5) 3
(-2,-
2)
NaN 100 (3,0.5) 10 (3,0.5) 8 varying 100 (3,0.5) 7 (3,0.5) 7 (3,0.5)
4
(3,0.5)
4
(-4,-
4)
(3,0.5) 117 (3,0.5) 10 (3,0.5) 15 (3,0.5) 10 (3,0.5) 10 (3,0.5) 12
(4.7703
,0.7383
) 1
(4.7188
,0.7384
) 4
(-6,-
6)
(20.66,
0.95)
50 (3,0.5) 21 NaN 100
(-
113.86,
1.0074)
8 (3,0.5) 21 varying 100
(6.842,.
832)
(6.79,0.
83)
3
For range of alpha between -50 to 50 alpha as well as x oscillates between large range probably because it gets distracted
too much in some iteration steps and converges very slowly sometimes.

20. Ackley function
2 2
0.2 0.5( ) 0.5(cos(2 ) cos(2 ))
( , ) 20 20x y x y
f x y e e e
3d plot of Ackley function

21. Ackley function
Contour plot of Ackley function

22. Ackley function
Initial
Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0)
Infinite Infinite Infinite Infinite Infinite Infinite
(1,1)
(0.9685,
0.9685)
4
(-0.9685,
-0.9685)
3 (-57,-57) 2
(0.9685,
0.9685)
4
(-0.9685,
-0.9685)
3 (-57,-57) 2
(3,3)
(0.9685,
0.9685)
4
(-1.9745,
-1.9745
3 (-82,-82) 4
(0.9685,
0.9685)
4
(-1.9745,
-1.9745
3 (-82,-82) 4
(5,5)
(-0.9685,
-0.9685)
4
(-1.9745,
-1.9745
4 (83,83) 4
(-0.9685,
-0.9685)
4
(-1.9745,
-1.9745
4 (83,83) 4
(-2,-2)
(-0.9685,
-0.9685)
4
(-1.9745,
-1.9745
3 (83,83) 4
(-0.9685,
-0.9685)
4
(-1.9745,
-1.9745
3 (83,83) 4
(-4,-4)
(-0.9685,
-0.9685)
4
(1.9745,
1.9745)
4 (-83,-83) 4
(-0.9685,
-0.9685)
4
(1.9745,1
.9745)
4 (-83,-83) 4
(-6,-6)
(-0.9685,
-0.9685)
2
(-1.9745,
-1.9745
4 (-83,-83) 4
(-0.9685,
-0.9685)
2
(-1.9745,
-1.9745
4 (-83,-83) 4
At(0,0) gradient of f(x,y) in not defined and hence the result shows Infinite
α=(-50,50) gives local minima which are far away from the initial point.
P-R and F-R gives exactly same results for all α and all initial points.

23. Ackley function
Initia
l
Point
Davidon-Fletcher-Powell (DFP) method
Broyden-Fletcher-Goldfarb-Shanno (BFGS)
method Powell's conjugate direction method
α α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterati
ons
Final
Point
# of
iteratio
ns
Final
Point
# of
iteratio
ns
Final
Point
# of
iteratio
ns
Final
Point
# of
iteratio
ns
Final
Point
# of
iteration
s
Final
Point
# of
iteratio
ns
Final
Point
# of
iteratio
ns
Final
Point
# of
iterations
(0,0)
NaN 100 NaN 100 NaN 100 NaN 100 NaN 100 NaN 100
oscillati
ng
oscillati
ng
oscillatin
g
but it has
been
identifie
d that
(1,1)
(.96885,
.9685)
4
(-
.96885,
-.9685)
3
(-57,-
57)
2
(.96885,
.9685)
4
(-
.96885,-
.9685)
3
(-57,-
57)
2
oscillati
ng
oscillati
ng
oscillatin
g
it has
function
(3,3)
(.96885,
.9685)
4
(5.9887
,5.9887
)
4
(.96885,
.9685)
4
(.96885,
.9685)
4
(5.9887,
5.9887)
4
(.96885,
.9685)
4
oscillati
ng
oscillati
ng
oscillatin
g
value
zero
(5,5)
(49,49) 4 (0,0) 6
(-295,-
295)
4 (49,49) 4 (0,0) 6
(-274,-
274)
4
oscillati
ng
oscillati
ng
oscillatin
g
or nearly
zero
(-2,-
2)
(-
.96885,-
.9685)
4 (0,0) 6 (0,0) 5
(-
.96885,-
.9685)
3 (0,0) 6 (0,0) 5
oscillati
ng
oscillati
ng
oscillatin
g
at
several
points
(-4,-
4)
(.96885,
.9685)
4
(.96885
,.9685)
4
(.96885,
.9685)
4
(-17,-
17)
4
(.96885,
.9685)
4
(.96885,
.9685)
4
oscillati
ng
oscillati
ng
oscillatin
g
(-6,-
6)
(-
.96885,-
.9685)
3
(-
.96885,
-.9685)
4 (0,0) 6
(-
.96885,-
.9685)
2
(-
.96885,-
.9685)
4 (0,0) 5
oscillati
ng
varying varying

24. It can be perceived from Powell’s method that Ackley fn has local minima at
several points
But as the algorithm reaches that point algorithm does not stop, it just oscillates
around it and one can guess that it happens possibly due to large range of alpha
(the function has several local minima within a very short distance) and this
perception was validated when the algorithm reached to local or global
minimum points when we ran the algorithm for small range of alpha (-2,3)
starting from several starting points!
For alpha (-5,20) the value sometimes almost reaches the minima but
then bounce back to another point not close to the previous point
Ackley function

25. In Powell method for Ackley function for range of alpha (-2,3) it happily reached
A minima at (0,0) within 2 iterations though powell’s method did not work well
for large range of alpha
x
y
Ackley function

26. Goldstein-Price function
2 2 2 2 2 2
( , ) (1 ( 1) (19 14 3 14 6 3 ))(30 (2 3 ) (18 32 12 48 36 27 ))f x y x y x x y xy y x y x x y xy y
3d plot of Goldstein-Price function

27. Goldstein-Price function
Contour plot of Goldstein-Price function

28. Goldstein-Price function
Initial
Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0)
Infinite (0,-1) 11 (0,-1) 25 Infinite (0,-1) 8 (0,-1) 9
(1,1)
Infinite (0,-1) 15 (0,-1) 19 Infinite (0,-1) 10 (0,-1) 26
(3,3)
Infinite Infinite (0,-1) 18 Infinite Infinite (0,-1) 34
(5,5)
Infinite Infinite (0,-1) 39 Infinite Infinite (0,-1) 22
(-2,-2)
Infinite Infinite (0,-1) 33 Infinite Infinite (0,-1) 10
(-4,-4)
Infinite Infinite (0,-1) 49 Infinite Infinite (0,-1) 11
(-6,-6)
Infinite Infinite
Does not
converge
Infinite Infinite
Does not
converge
 α=(-50,50) works better compared to other α ranges.
Changing α to(-100,100) results in convergence for (-6,-6) initial point also.

29. Goldstein-Price function
DFP and BFGS gives better result (less # of iterations) compared to F-R and P-R .
Initial
Point
Davidon-Fletcher-Powell (DFP) method
Broyden-Fletcher-Goldfarb-Shanno (BFGS)
method
Powell's conjugate direction method
α α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iteratio
ns
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0) (0,-1) 12 (0,-1) 6 (0,-1) 5 (0,-1) 12 (0,-1) 6 (0,-1) 5
oscillatin
g
(0,-1) 1
(0,-
.999)
1
(1,1)
(1.8,0.
2)
12 (1.8,2) 6 (0,-1) 7
(1.8,0.
2)
12 (1.8,2) 6 (0,-1) 7 (2.986,1) 2 (0,-1) 4
(0.003,
-.99)
1
(3,3) NaN 100 NaN 100 (0,-1) 11 NaN 100 (0,-1) 17 (0,-1) 11
oscillatin
g
(0,-1) 2 (0,-1) 5
(5,5) NaN 100 NaN 100 (0,-1) 11 NaN 100 (0,-1) 17 (0,-1) 12 (0,-1) 3 (0,-1) 3
(-2,-
2)
(0,-1) 16 (0,-1) 32
(-.6,-
.4)
7 (0,-1) 16 (0,-1) 12
(-.6,-
.4)
7
(2.497,
.675)
4
(-.6,-
.4)
3 (0,-1) 4
(-4,-
4)
NaN 100
(-.6,-
.4)
22 (0,-1) 16 NaN 100 (0,-1) 14 (0,-1) 11
(2.9933
0.9896)
3 (0,-1) 3
oscillat
ing
(-6,-
6)
NaN 100 NaN 100 (0,-1) 10 NaN 100 (0,-1) 17 (0,-1) 10
(1.8434
0.2297)
3 (0,-1) 3*3 (0,-1) 3

30. Cross-in-tray function
2 2
0.1
100
( , ) 0.0001 sin( )sin( ) 1
x y
f x y x y e
3d plot of Cross-in -Tray function

31. Cross-in-tray function
Contour plot of Cross-in -Tray function

32. Cross-in-tray function
Initial
Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0) Infinite Infinite Infinite Infinite Infinite Infinite
(1,1)
(1.3494,
1.3494)
2
(1.3494,
1.3494)
2
(1.3494,
1.3494)
2
(1.3494,
1.3494)
2
(1.3494,
1.3494)
2
(1.3494,
1.3494)
2
(3,3)
(1.3494,
1.3494)
2
(-1.3494,
-1.3494)
2
(-1.3494,
-1.3494)
2
(1.3494,
1.3494)
2
(-1.3494,
-1.3494)
2
(-1.3494,
-1.3494)
2
(5,5)
(4.4910,
4.4910)
2
(4.4910,
4.4910)
2
(4.4910,
4.4910)
2
(4.4910,
4.4910)
2
(4.4910,
4.4910)
2
(4.4910,
4.4910)
2
(-2,-2)
(-1.3494,
-1.3494)
2
(-1.3494,
-1.3494)
2
(1.3494,
1.3494)
2
(-1.3494,
-1.3494)
2
(-1.3494,
-1.3494)
2
(1.3494,
1.3494)
2
(-4,-4)
(-4.4910,
-4.4910)
2
(-4.4910,
-4.4910)
2
(-4.4910,
-4.4910)
2
(-4.4910,
-4.4910)
2
(-4.4910,
-4.4910)
2
(-4.4910,
-4.4910)
2
(-6,-6)
(-4.4910,
-4.4910)
2
(-1.3494,
-1.3494)
2
(-1.3494,
-1.3494)
2
(-4.4910,
-4.4910)
2
(-1.3494,
-1.3494)
2
(-1.3494,
-1.3494)
2
At(0,0) gradient of f(x,y) in not defined and hence the result shows Infinite
For α=(0,10), positive initial point gives positive local minima only which
is not the case for other α.

33. Cross-in-tray function
All methods give local minima closest to initial point.
Davidon-Fletcher-Powell (DFP) method Broyden-Fletcher-Goldfarb-Shanno (BFGS) method Powell's conjugate direction method
α α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iteration
s
Final
Point
# of
iteratio
ns
Final
Point
# of
iteratio
ns
Final
Point
# of
iterations
Final
Point
# of
iteration
s
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
NaN NaN NaN NaN
NaN NaN
oscillati
ng
(0,-1) 1 oscillati
ng
(1.3494,
1.3494)
2
(1.3494,
1.3494)
2
(1.3494,
1.3494)
2
(1.3494
,1.3494
)
2
(1.3494,
1.3494)
2
(1.3494
,1.3494
)
2 oscillati
ng
(0,-1) 4 oscillati
ng
(1.3494,
1.3494)
2
(-1.3494,-
1.3494)
2
(-1.3494,
-1.3494)
2
(1.3494
,1.3494
)
2
(-1.3494,
-1.3494)
2
(-
1.3494,
-
1.3494)
2
oscillati
ng
(0,-1) 2
oscillati
ng
(4.491,
4.491)
2
(4.491,
4.491)
2
(4.491,
4.491)
2
(4.491,
4.491)
2
(4.491,
4.491)
2
(4.491,
4.491)
2 oscillati
ng
(0,-1) 3 oscillati
ng
(-1.3494,
-1.3494)
2
(-1.3494,-
1.3494)
2
(1.3494,
1.3494)
2
(-
1.3494,
-
1.3494)
2
(-1.3494,
-1.3494)
2
(1.3494
,1.3494
)
2
oscillati
ng
(-.6,-.4) 3
oscillati
ng
(-4.491,
-4.491)
2
(-4.491,-
4.491)
2
(-4.491,-
4.491)
2
(-
4.491,-
4.491)
2
(-4.491,-
4.491)
2
(-
4.491,-
4.491)
2 oscillati
ng
(0,-1) 3 oscillati
ng
(-4.491,
-4.491)
2
(-1.3494,-
1.3494)
2
(-1.3494,-
1.3494)
2
(-
4.491,-
4.491)
2
(-
1.3494,-
1.3494)
2
(-
1.3494,
-
1.3494)
2
oscillati
ng
(0,-1) 3*3
oscillati
ng

34. Bukin function
2
( , ) 100 | 0.01 | 0.01| 10|f x y y x x
3d plot of Bukin function

35. Bukin function
3d plot of Bukin function

36. Bukin function
Initial
Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0)
Infinite Infinite Infinite Infinite Infinite Infinite
(1,1)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(3,3)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(5,5)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(-2,-2)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(-4,-4)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(-6,-6)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge

37. Bukin function
x1
x2
Bukin’s function for (-2,-2) initial point and α=(-50,50) for F-R method

38. Bukin function
Initial
Point
Davidon-Fletcher-Powell (DFP) method Broyden-Fletcher-Goldfarb-Shanno (BFGS) method Powell's conjugate direction method
α α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iteration
s
Final
Point
# of
iteration
s
Final
Point
# of
iteration
s
Final
Point
# of
iteration
s
Final
Point
# of
iteration
s
Final
Point
# of
iteration
s
Final Point
# of
iterations
Final Point
# of
iterations
Final Point
# of
iterations
(0,0)
(-0.0162
0.0000) 1
(-0.0162
0.0000) 2
(-0.0162
0.0000) 1
(1,1)
(10,1) not
converging
properly 1
(10,1) not
converging
properly 1
varying or
oscillating
(3,3)
NOT
WORKI
NG
varying or
oscillating
varying
varying or
oscillating
(5,5)
varying or
oscillating
oscillating
varying or
oscillating
(-2,-2)
varying or
oscillating
(0,0)
1
varying or
oscillating
(-4,-4)
varying or
oscillating
converges
to(14.3248
2.0520)
but rhere
were some
points
having less
function
value 6
varying or
oscillating
(-6,-6)
varying or
oscillating
(-0.0162
0.0000)
1
varying or
oscillating

39. For Powell method alpha (-50,50) starting from (3,3) the ultimate point just oscillates fro
(-17.02,3) to (17.02,3)
x
y

40. Rosenbrock function
1
2 2 2
1
1
( ) {100( ) ( 1) }
n
i i i
i
f X x x x

41. Initial Point
Fletcher-Reeves Polak-Ribiere
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
Final
Point
# of
iterations
(0,0,0,0,0,0
,0,0)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(1,1,1,1,1,1
,1,1)
(1,1,1,1,1
,1,1,1)
1
(1,1,1,1,1
,1,1,1)
1
(1,1,1,1,1
,1,1,1)
1
(1,1,1,1,1
,1,1,1)
1
(1,1,1,1,1
,1,1,1)
1
(1,1,1,1,1
,1,1,1)
1
(3,3,3,3,3,3
,3,3)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(5,5,5,5,5,5
,5,5)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(-2,-2,-2,-
2,-2,-2,-2,-
2)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(-4,-4,-4,-
4,-4,-4,-4,-
4)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
(-6,-6,-6,-
6,-6,-6,-6,-
6)
Does not converge Does not converge Does not converge Does not converge Does not converge Does not converge
The point (1,1,1,1,1,1,1,1) is itself a minimum point and hence it
converges for that initial point only
Rosenbrock (8 variable) function

42. Rosenbrock (8 variable) function
F-R very slowly converges 10 the minimum point.
F-R method for α=(0,10) and (-2, -2, -2, -2, -2, -2, -2, -2) initial point

43. Initial
Point
Davidon-Fletcher-Powell (DFP) method Broyden-Fletcher-Goldfarb-Shanno (BFGS) method
α α
(0,10) (-5,20) (-50,50) (0,10) (-5,20) (-50,50)
Final Point
# of
iterations
and # of
function
evaluation
s Final Point
# of
iterations
and # of
function
evaluations Final Point
# of
iterations
and # of
function
evaluations Final Point
# of
iterations
and # of
function
evaluation
s Final Point
# of
iterations
and # of
function
evaluation
s Final Point
# of
iterations
and # of
function
evaluations
(0,0,0,0,
0,0,0,0)
(1,1,1,1,1,
1,1,1)
59
(1,1,1,1,1,
1,1,1)
45
(1,1,1,1,1,
1,1,1)
45
(1,1,1,1,1,
1,1,1)
46
(1,1,1,1,1,
1,1,1)
45
(1,1,1,1,1,
1,1,1)
45
(1,1,1,1,
1,1,1,1)
(1,1,1,1,1,
1,1,1)
1
(1,1,1,1,1,
1,1,1)
1
(1,1,1,1,1,
1,1,1)
1
(1,1,1,1,1,
1,1,1)
1
(1,1,1,1,1,
1,1,1)
1
(1,1,1,1,1,
1,1,1)
1
(3,3,3,3,
3,3,3,3)
slowly
converging
(1,1,1,1,1,
1,1,1)
44
(1,1,1,1,1,
1,1,1)
39
(1,1,1,1,1,
1,1,1)
31
(1,1,1,1,1,
1,1,1)
34
(1,1,1,1,1,
1,1,1)
37
(5,5,5,5,
5,5,5,5)
not
converging
or very
slowly
converging
(1,1,1,1,1,
1,1,1)
44
(1,1,1,1,1,
1,1,1)
271
(1,1,1,1,1,
1,1,1)
75
(1,1,1,1,1,
1,1,1)
48
(1,1,1,1,1,
1,1,1)
72
(-2,-2,-
2,-2,-2,-
2,-2,-2)
slowly
converging
/oscillating
(1,1,1,1,1,
1,1,1)
69
(1,1,1,1,1,
1,1,1)
65
(1,1,1,1,1,
1,1,1)
52
(1,1,1,1,1,
1,1,1)
54
(1,1,1,1,1,
1,1,1)
51
(-4,-4,-
4,-4,-4,-
4,-4,-4)
slowly
converging
/oscillating
(1,1,1,1,1,
1,1,1)
slowly
converging
/oscillating
(1,1,1,1,1,
1,1,1)
64
(1,1,1,1,1,
1,1,1)
56
(1,1,1,1,1,
1,1,1)
41
(1,1,1,1,1,
1,1,1)
56
(-6,-6,-
6,-6,-6,-
6,-6,-6)
(1,1,1,1,1,
1,1,1)
30
(1,1,1,1,1,
1,1,1)
126
(1,1,1,1,1,
1,1,1)
182
(1,1,1,1,1,
1,1,1)
23
(1,1,1,1,1,
1,1,1)
37
(1,1,1,1,1,
1,1,1)
62
Rosenbrock(8 variable) function

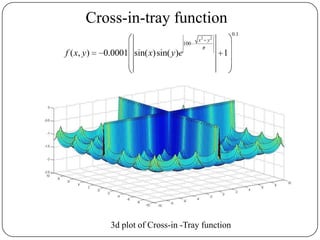
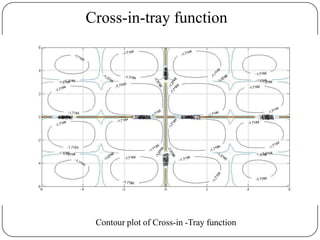
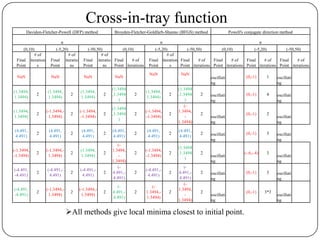
44. Conclusions
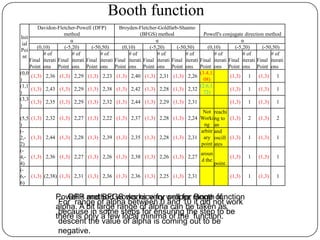
 For quadratic problems, all methods gives satisfactory results.
Powell’s method is working satisfactorily for small (i.e.lower-dimensional)
problems [particularly for α=(-5,20)]
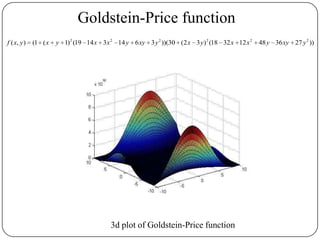
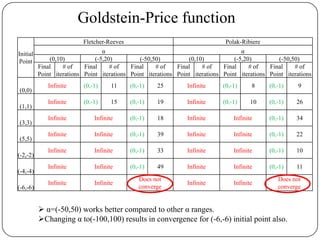
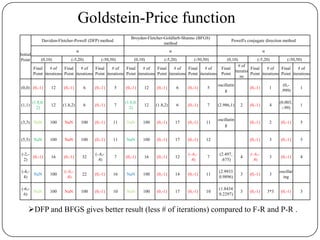
DFP-BFGS works very good for bad functions (e.g Goldstein Price
function) where F-R and P-R does not work well.
Suitability of DFP, BFGS for higher dimensional problems need to be
studied more.
Range of step size if chosen small and searches on both side of the given
point [α=(-5,20)], it works well for all problems.