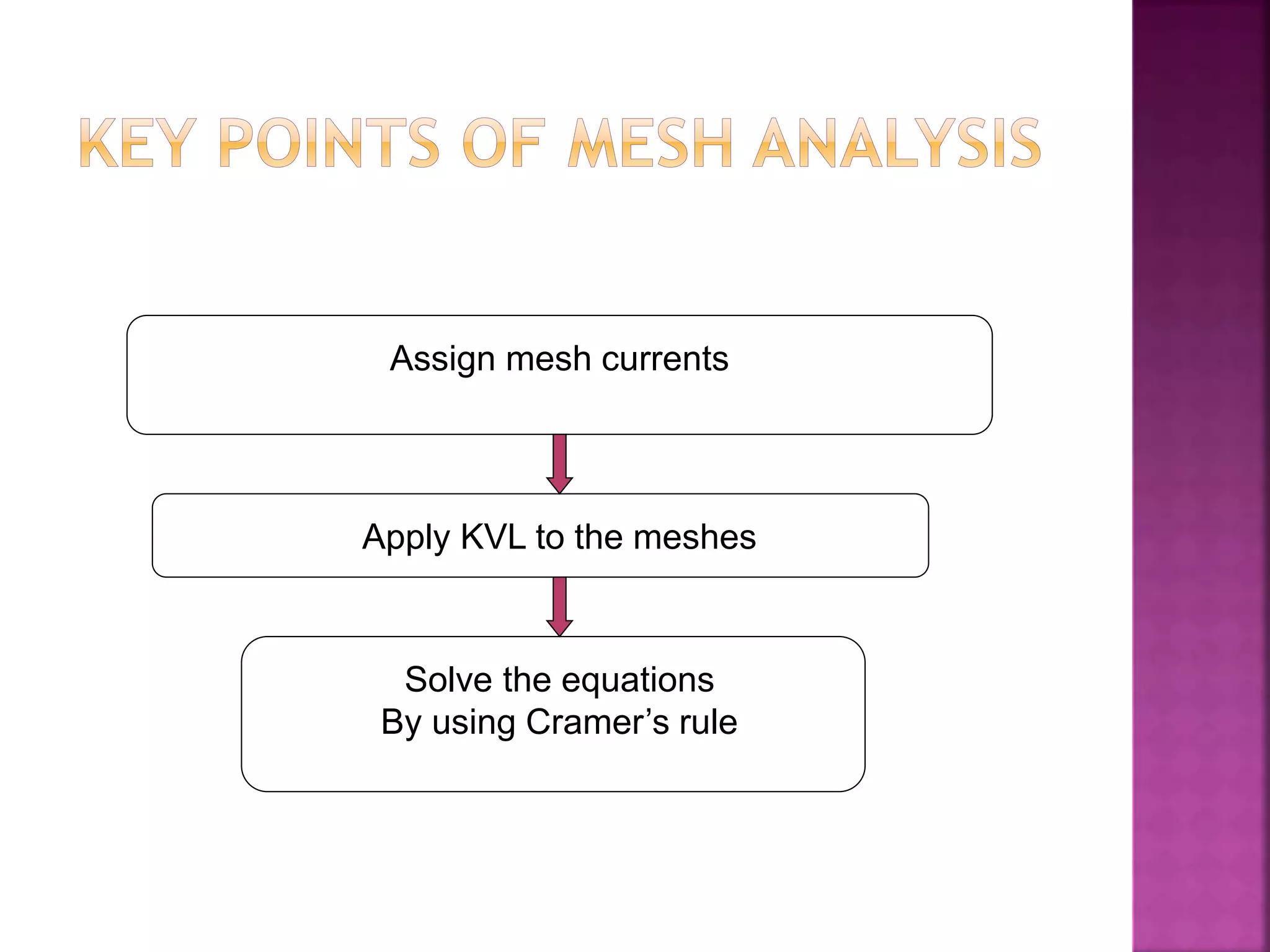
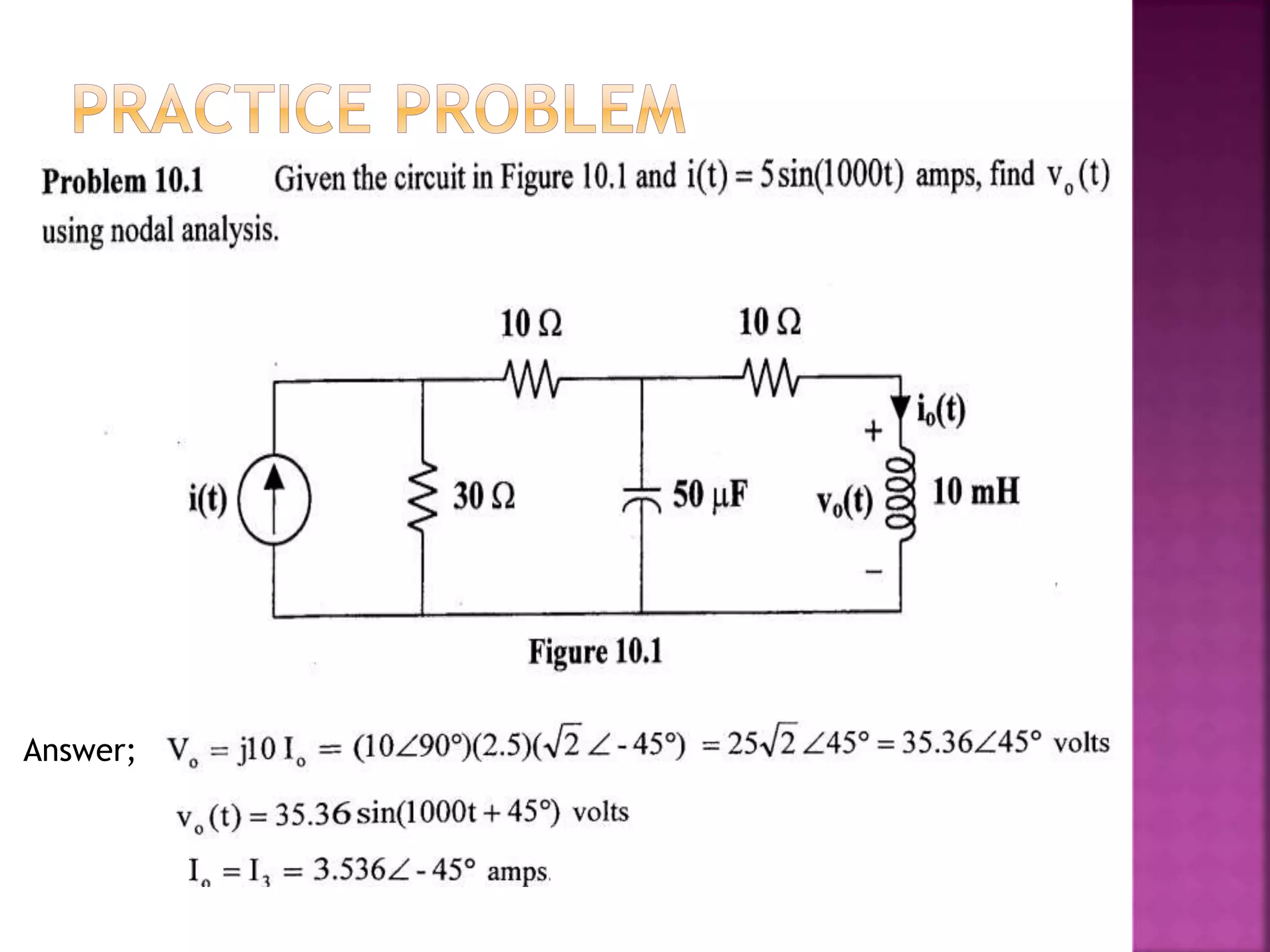
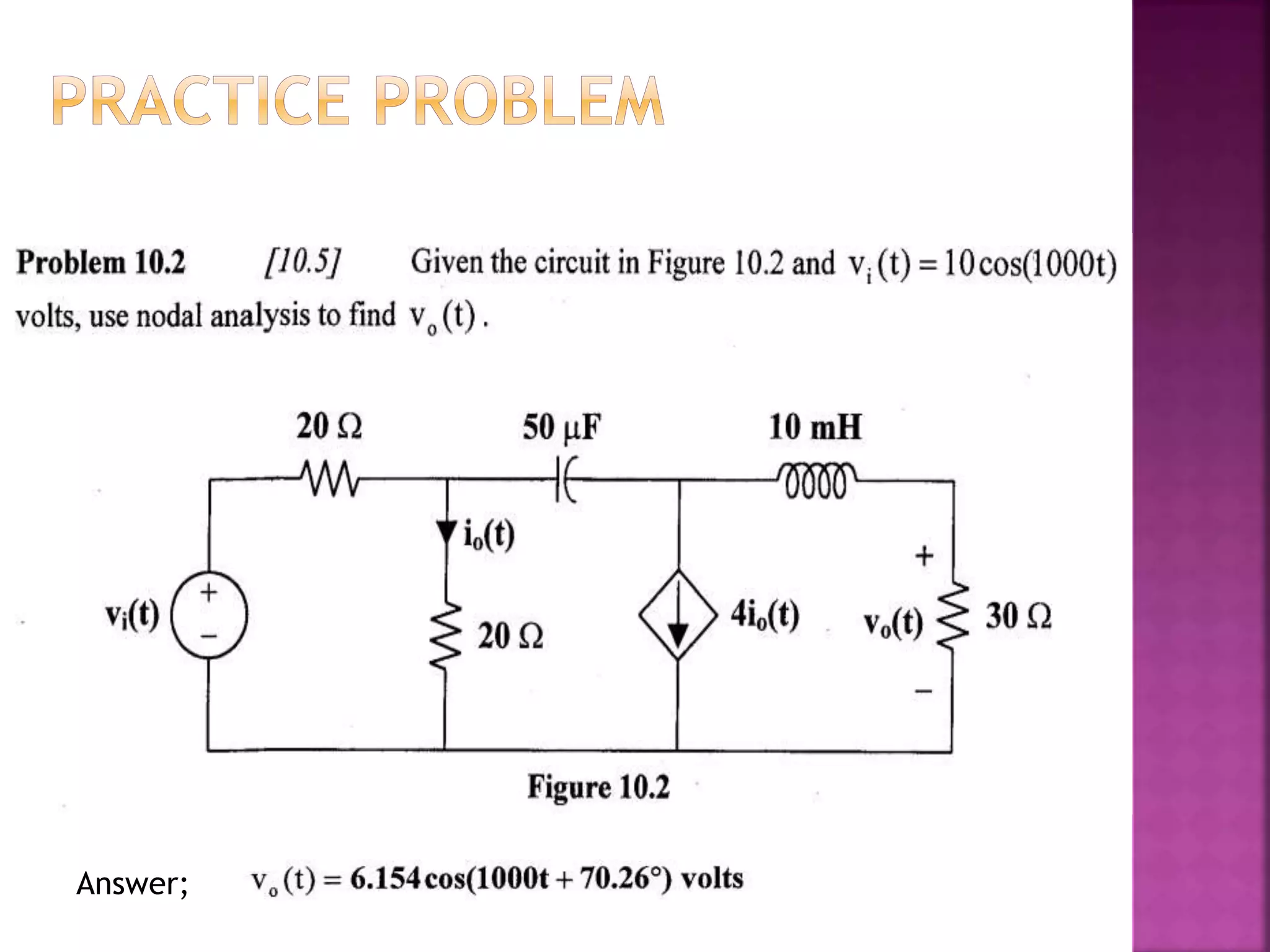
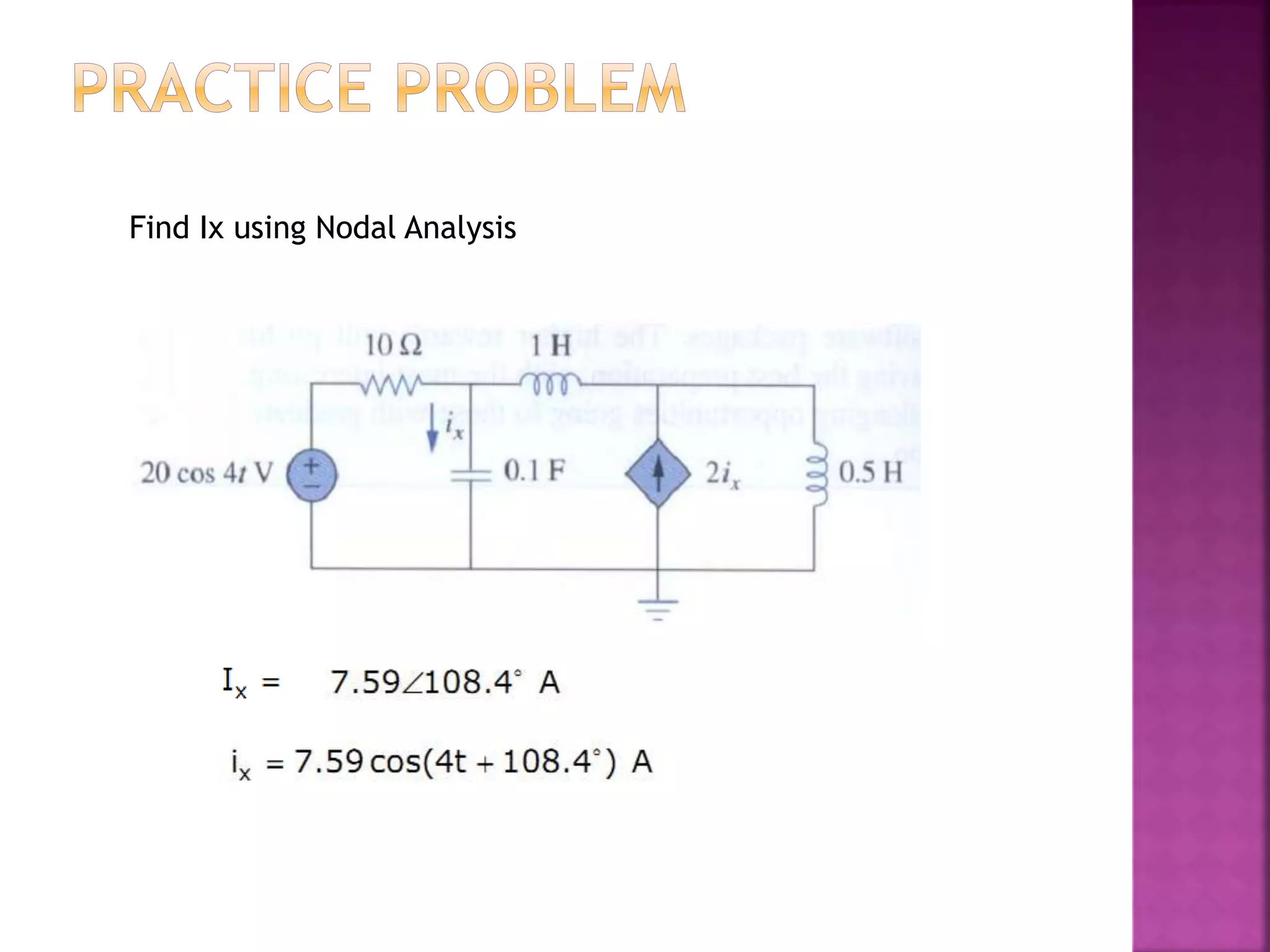
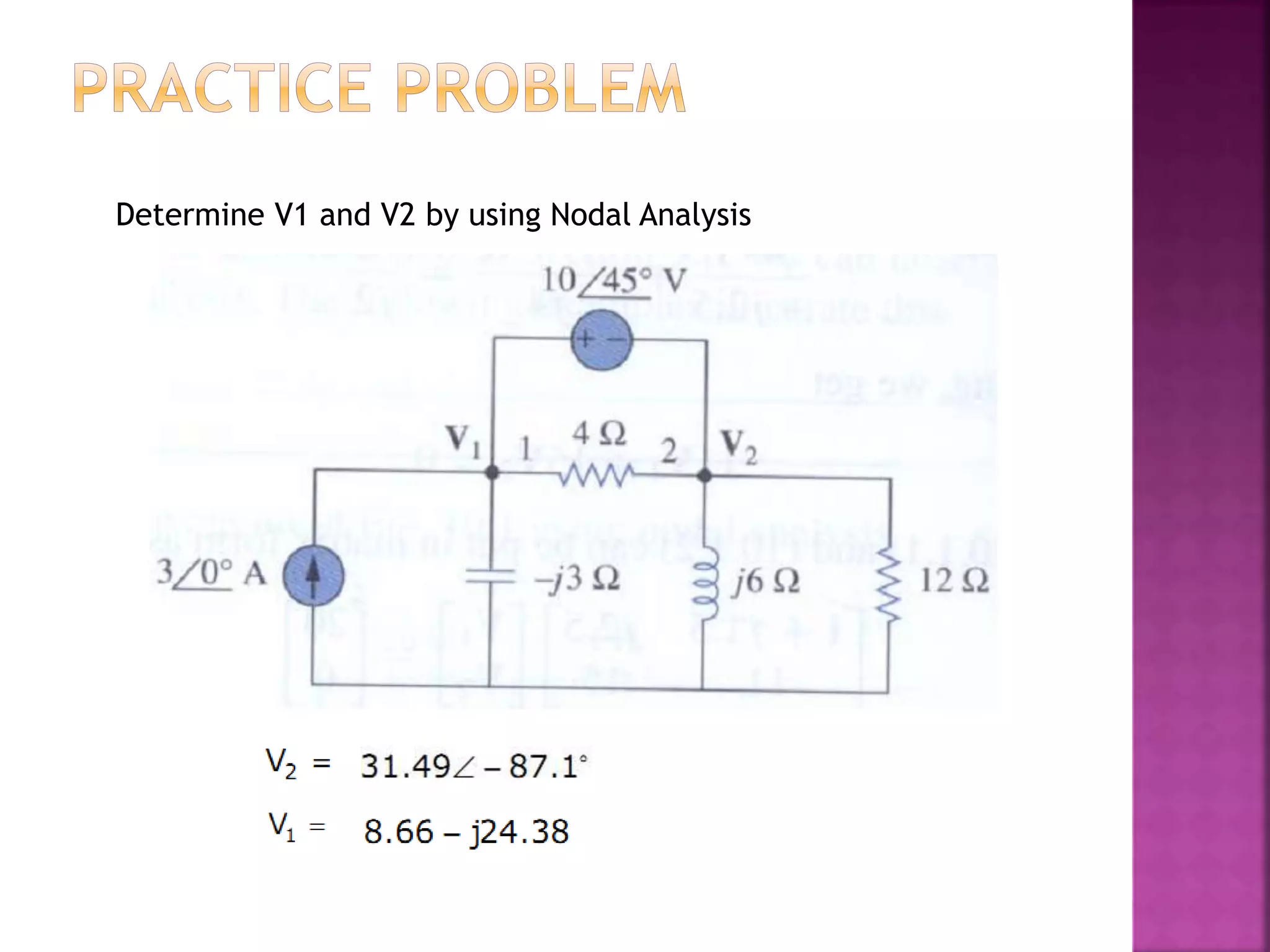
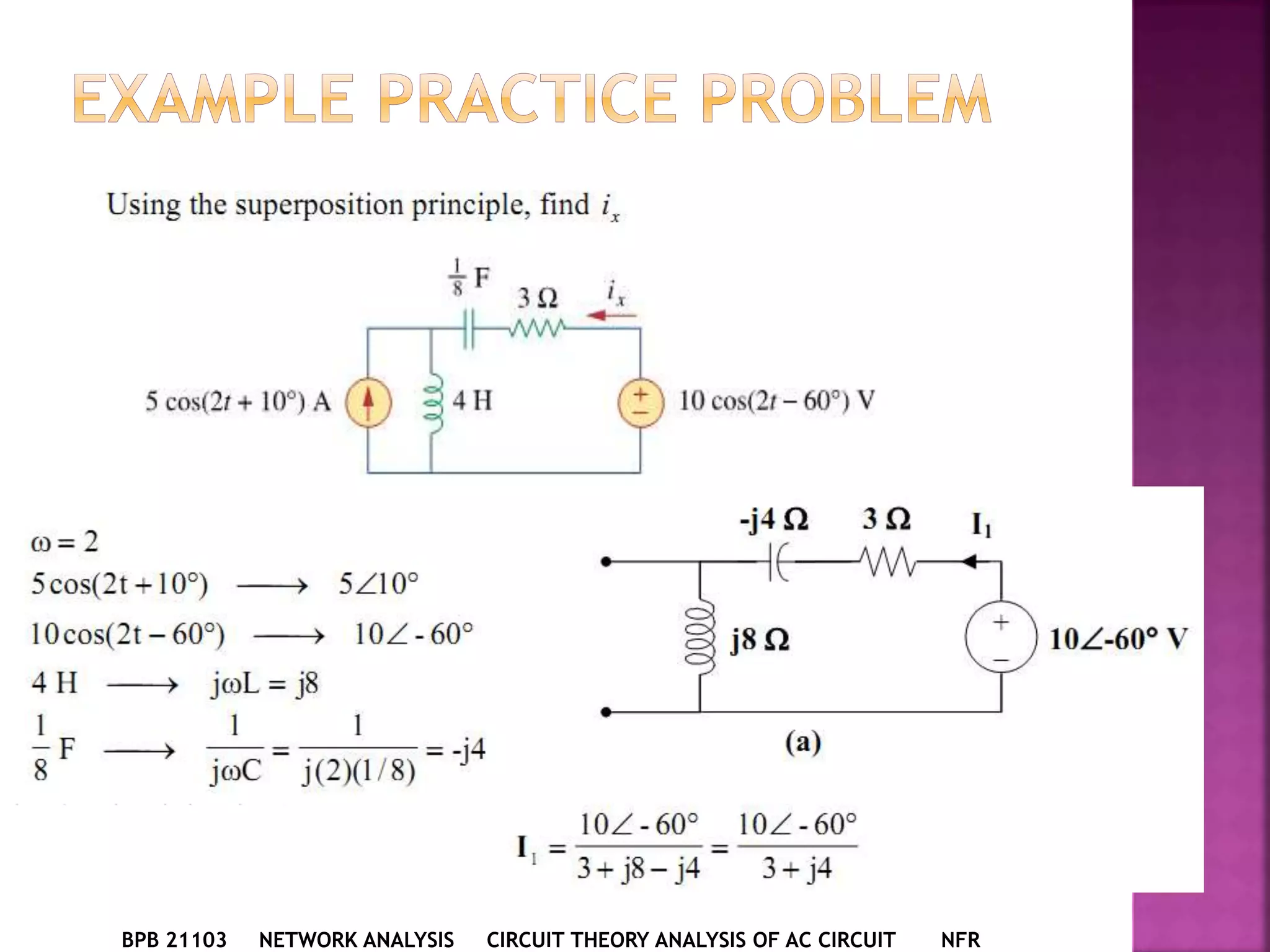
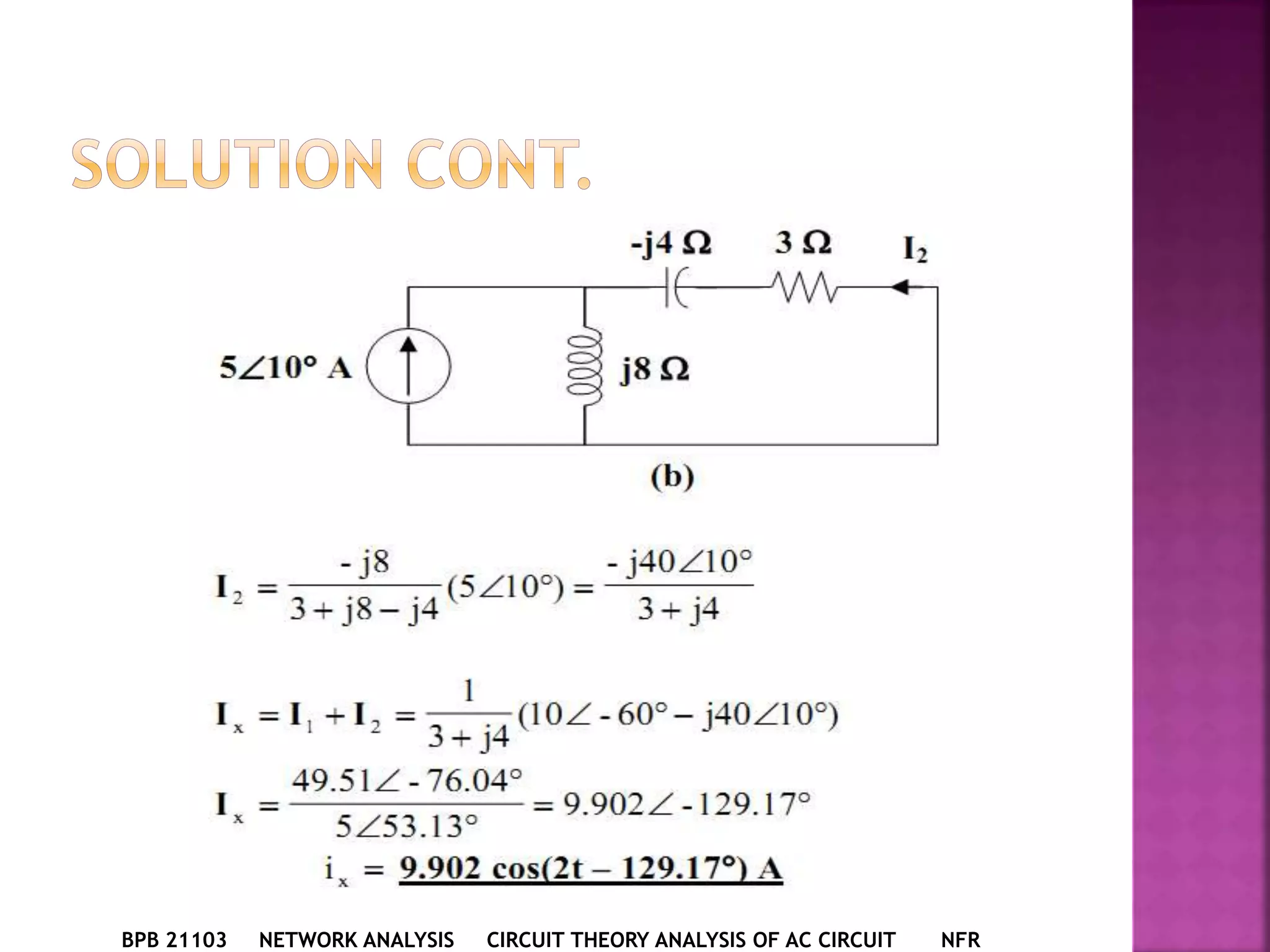
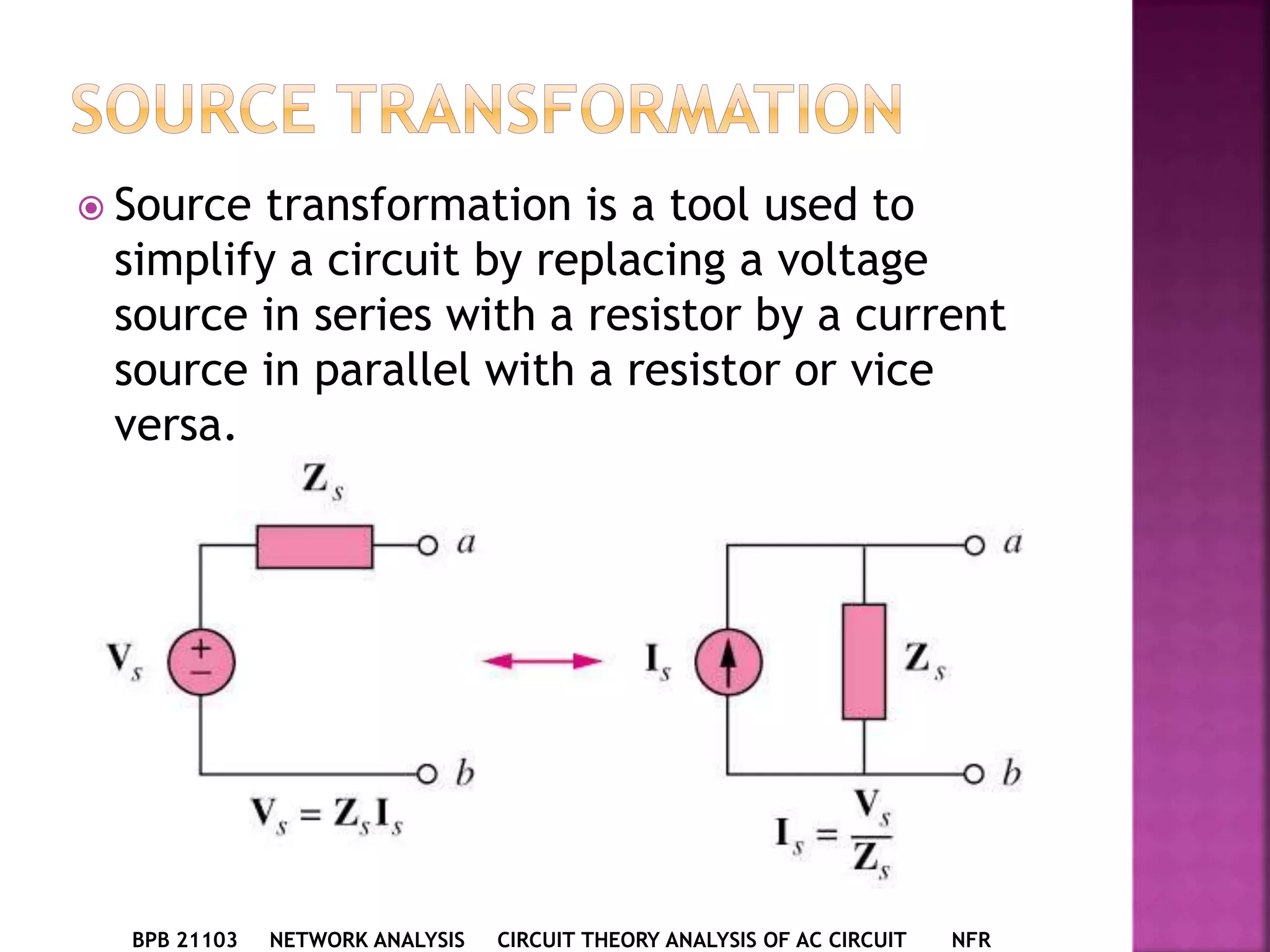
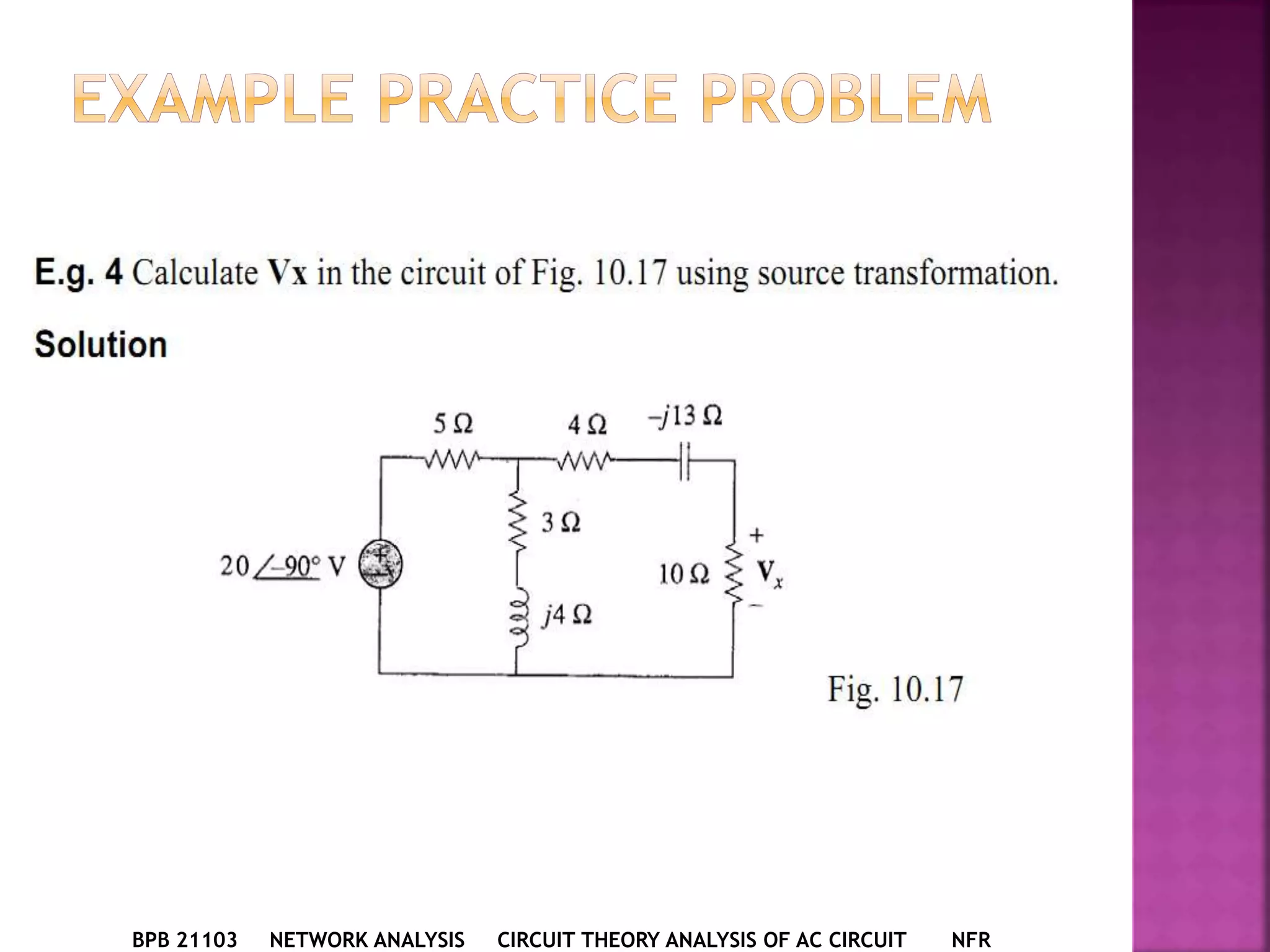
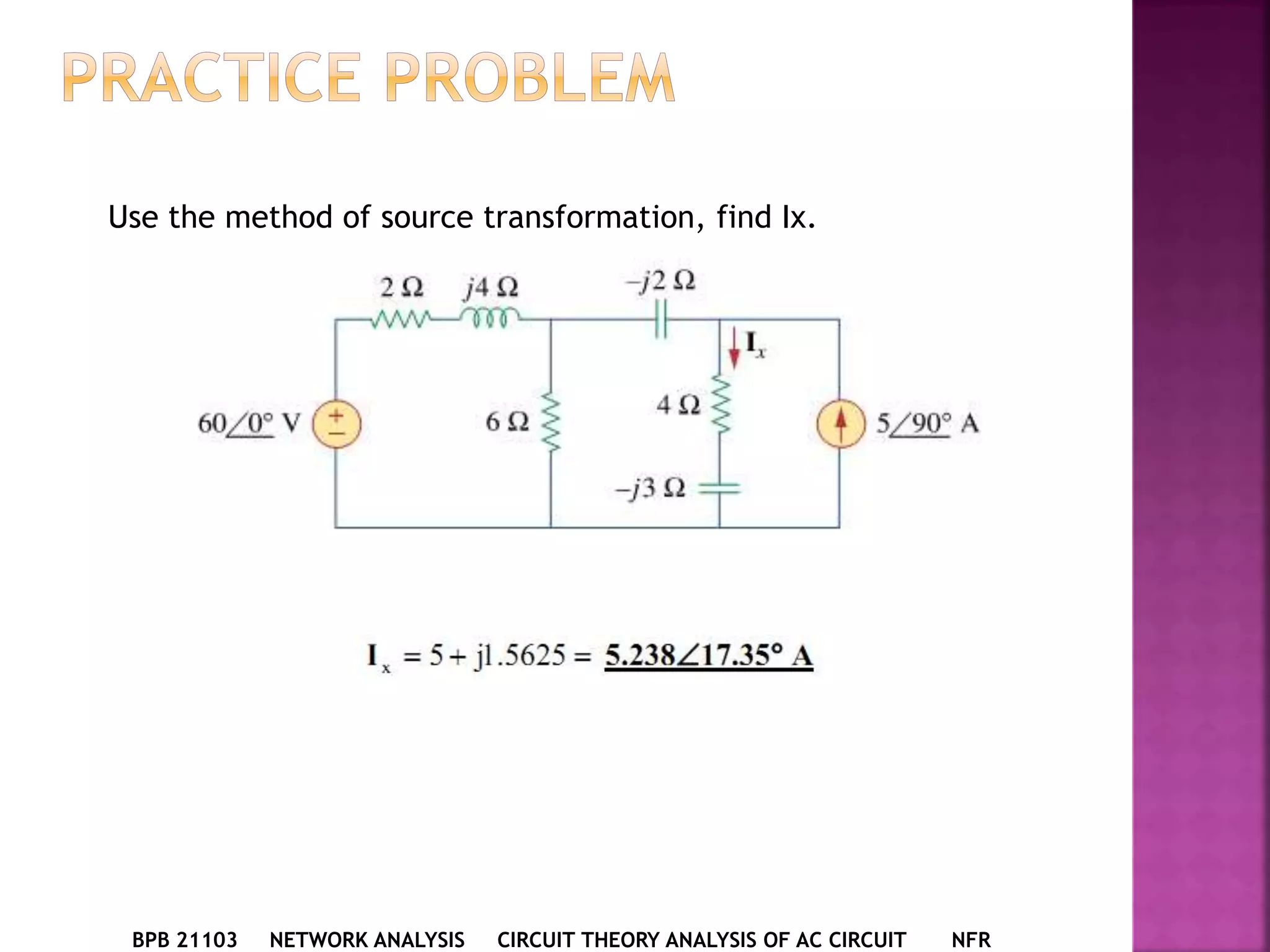
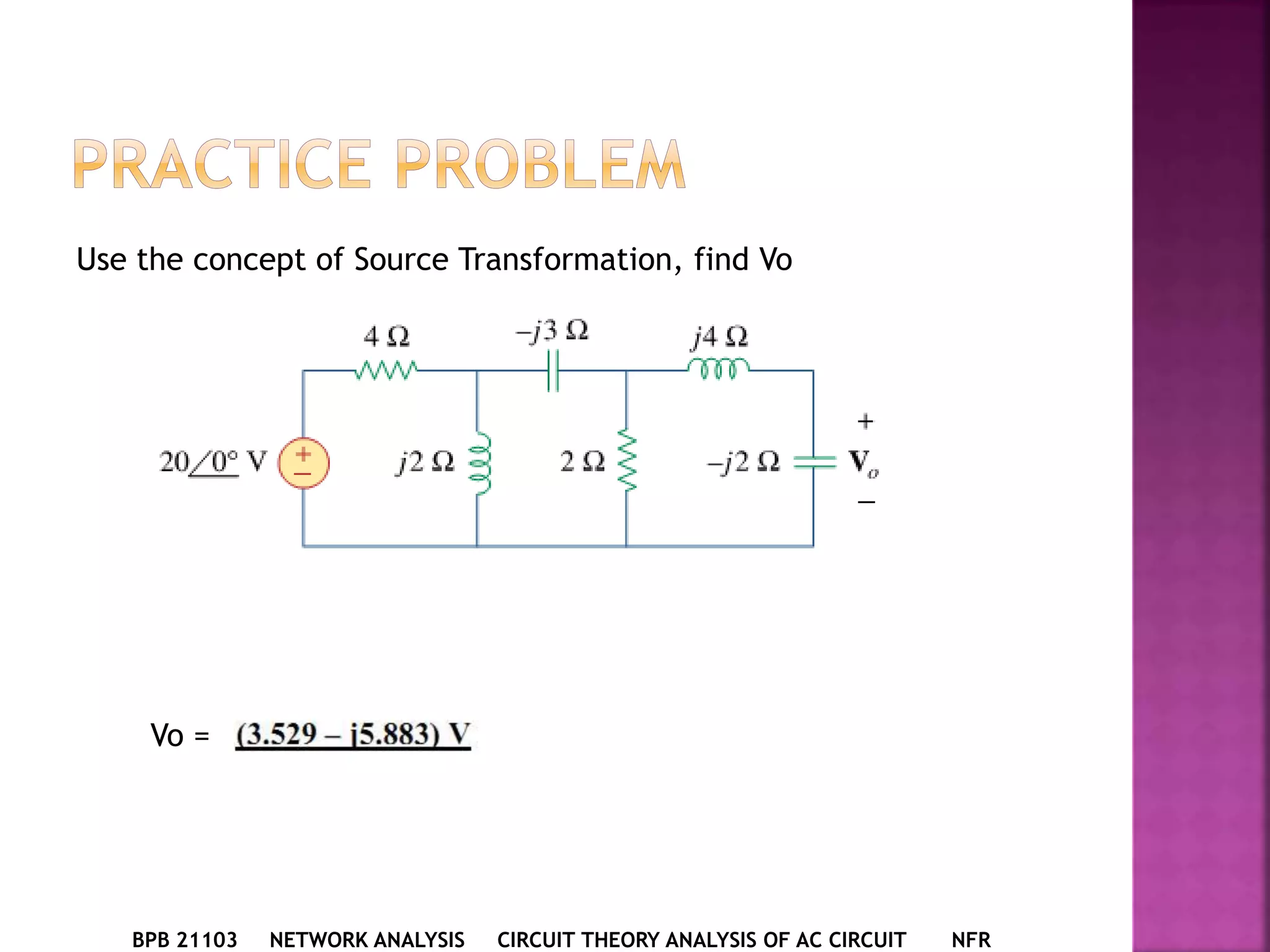
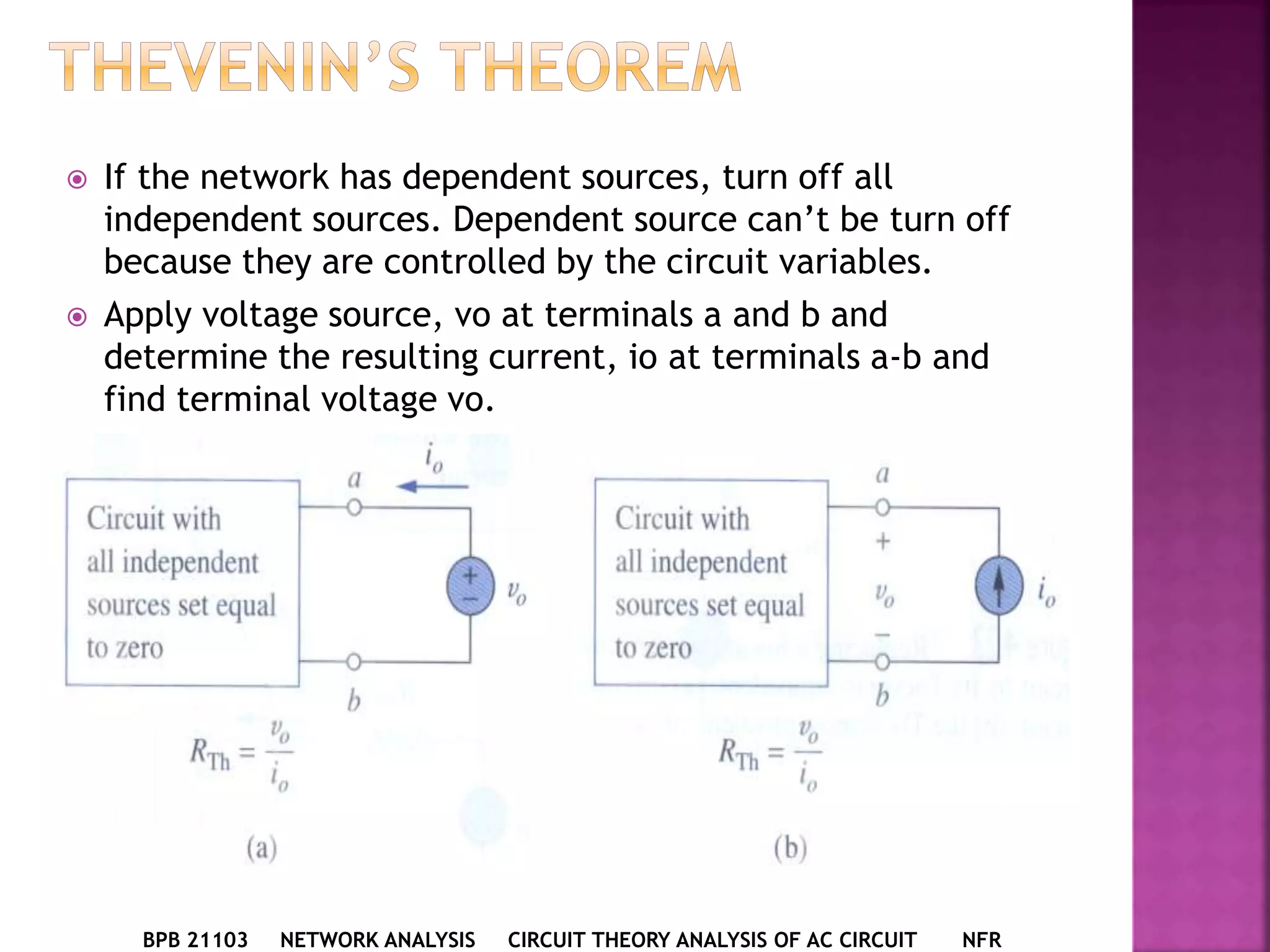
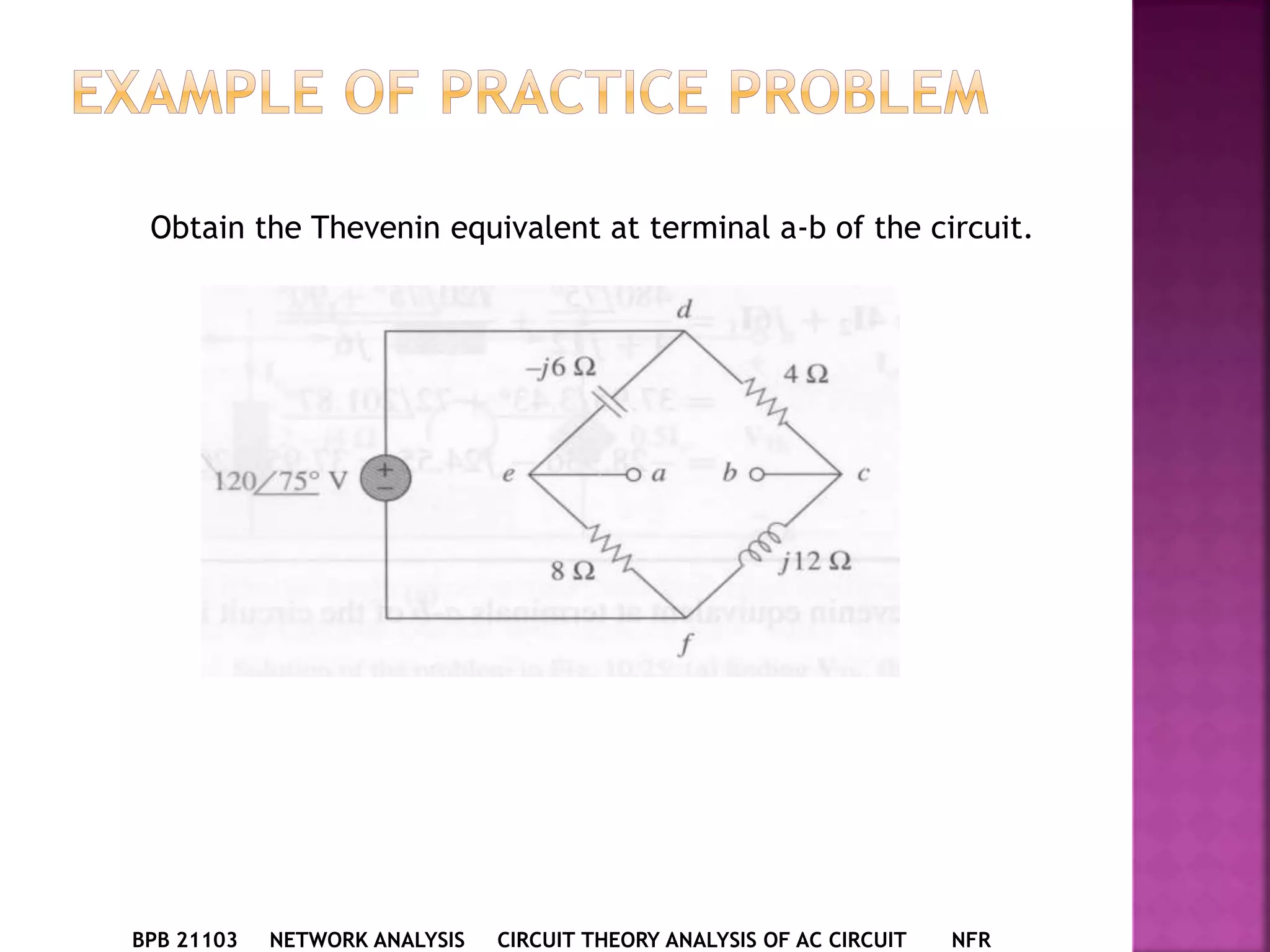
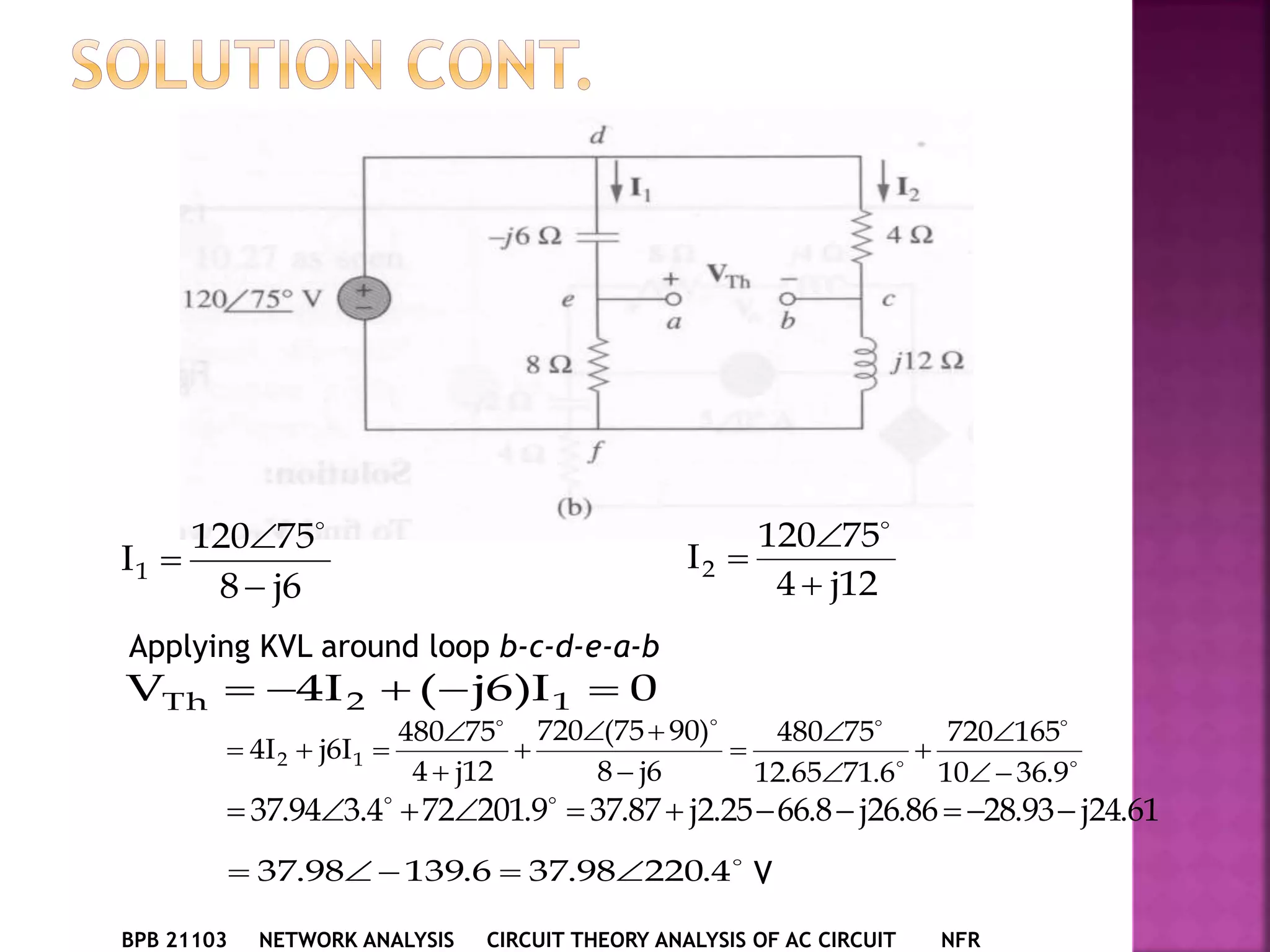
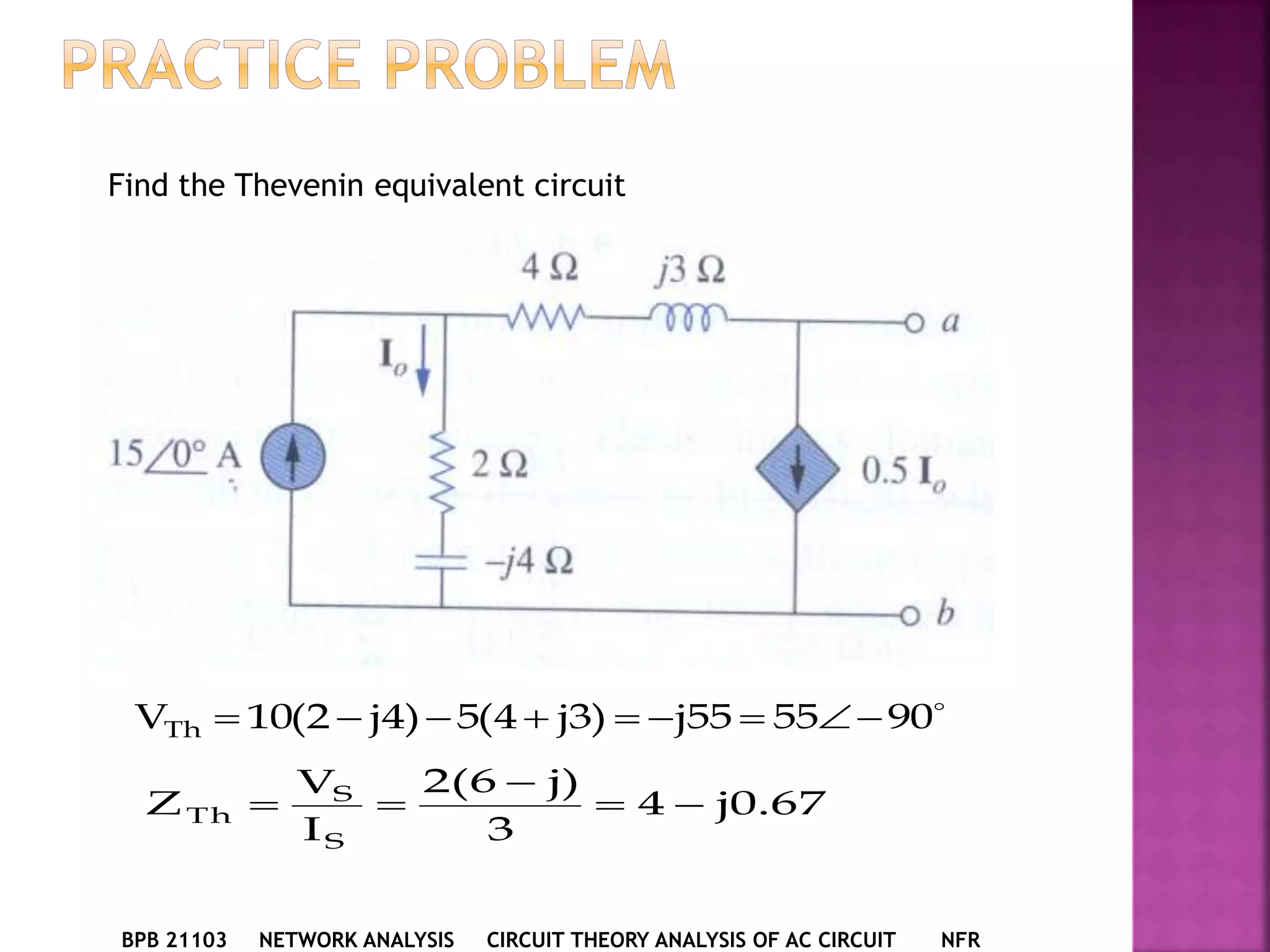
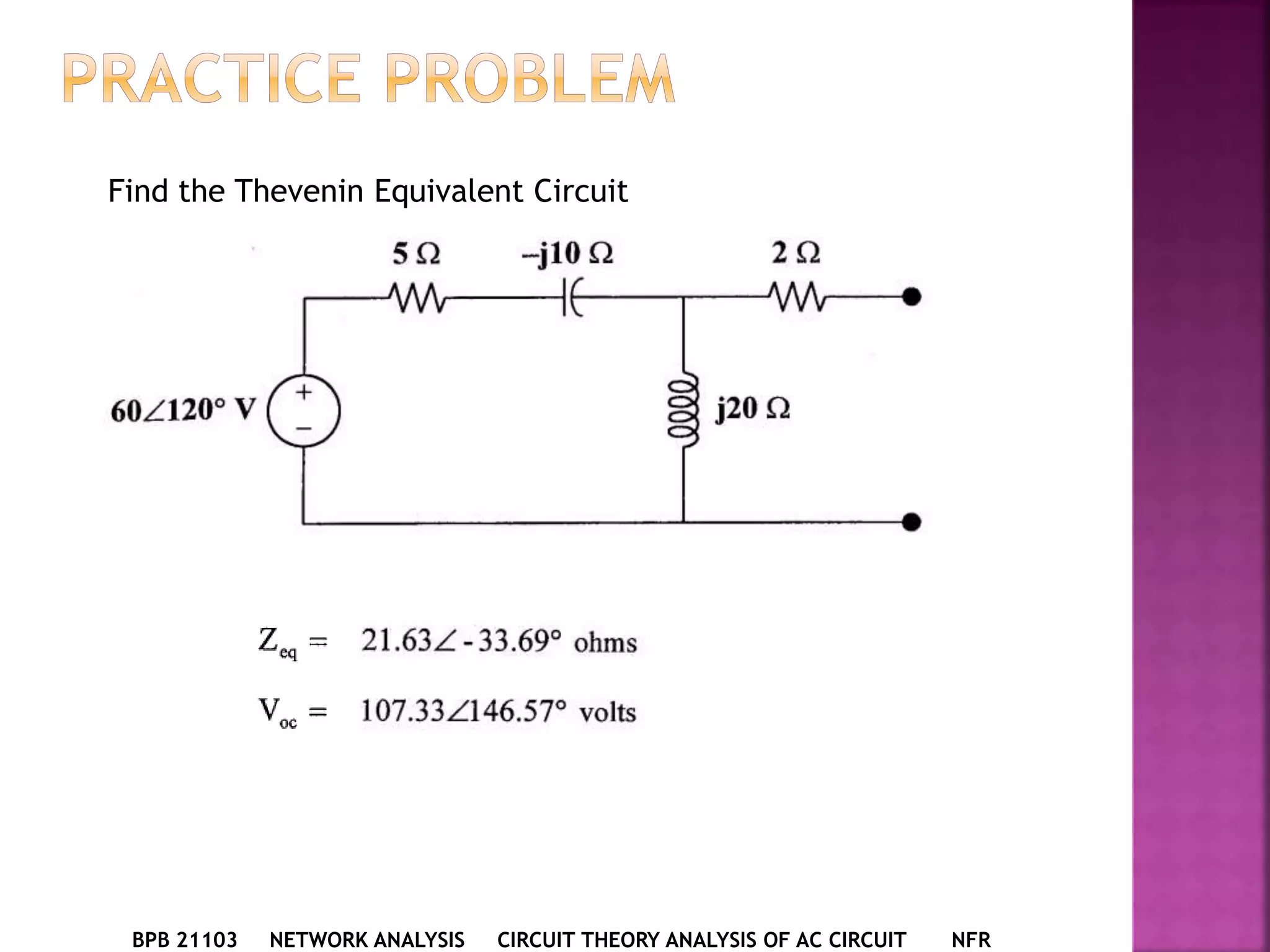
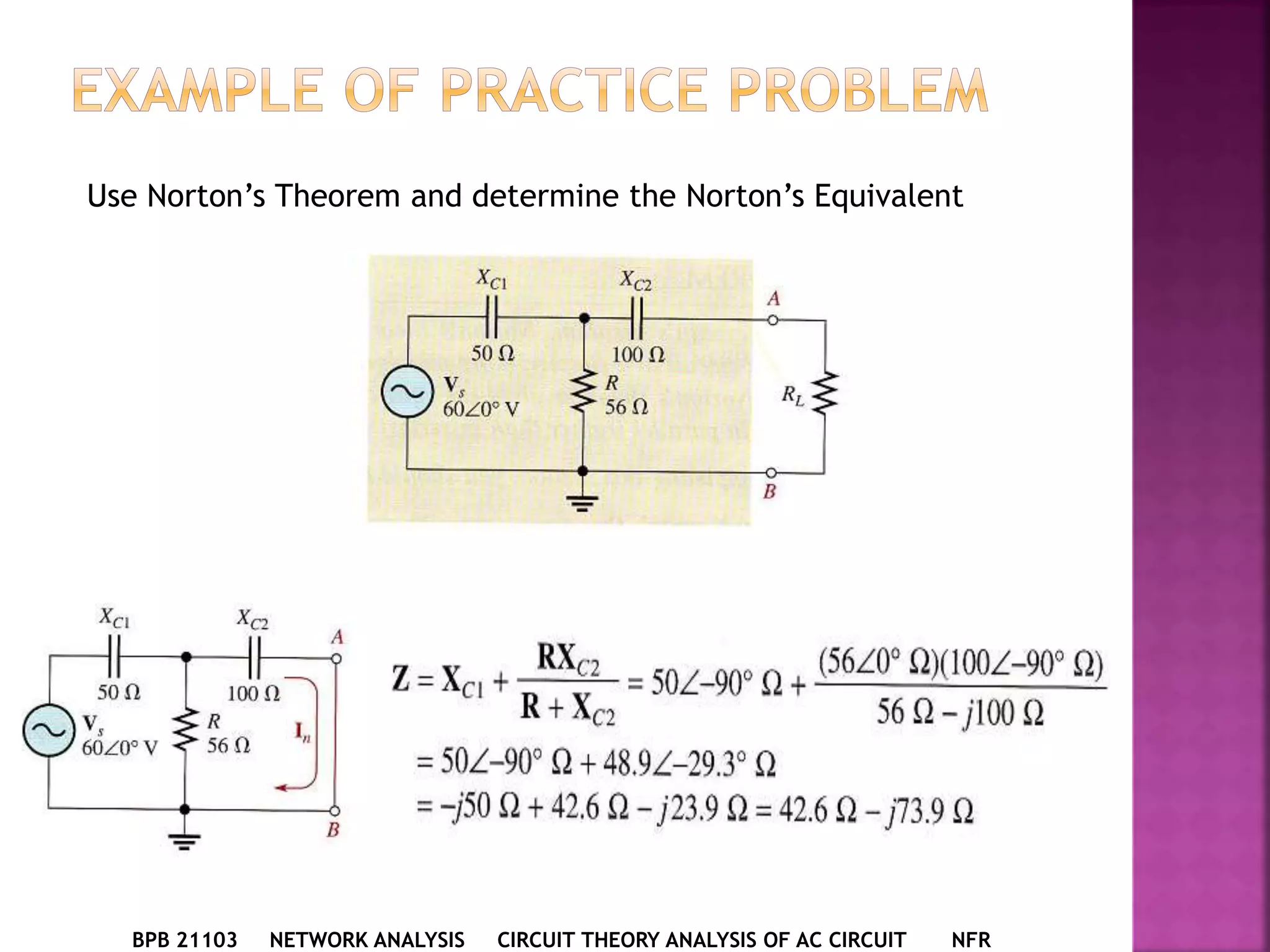
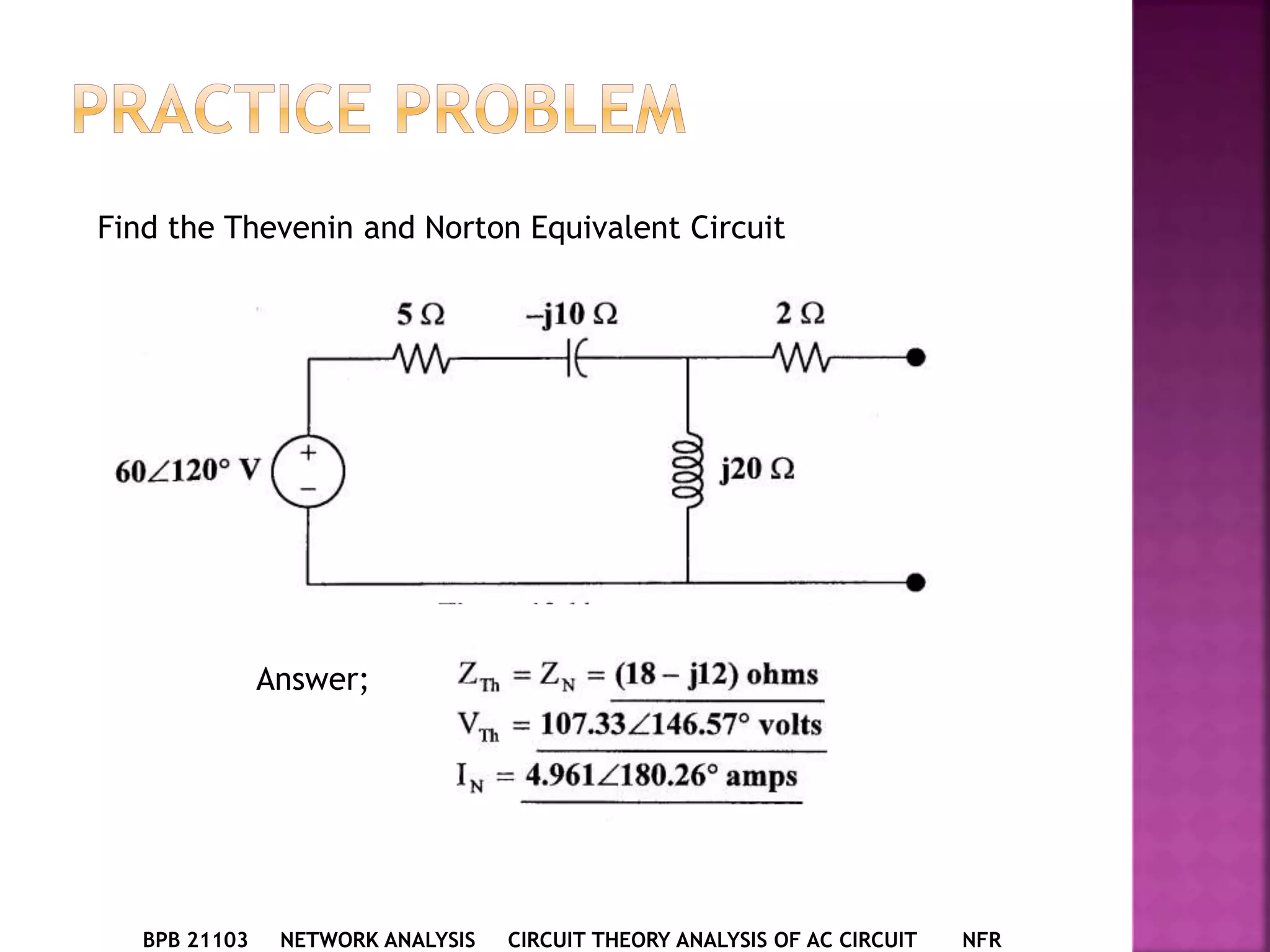
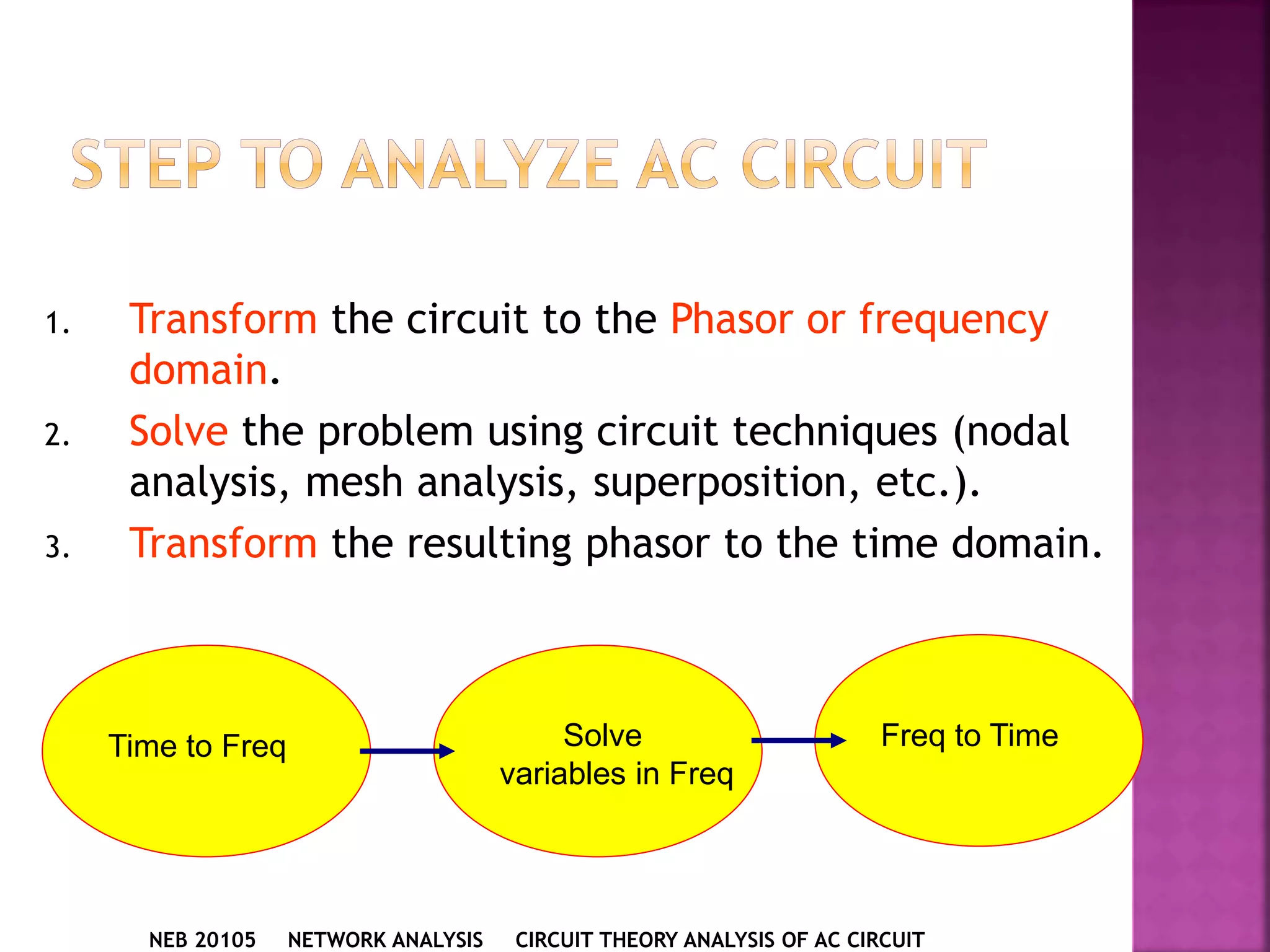
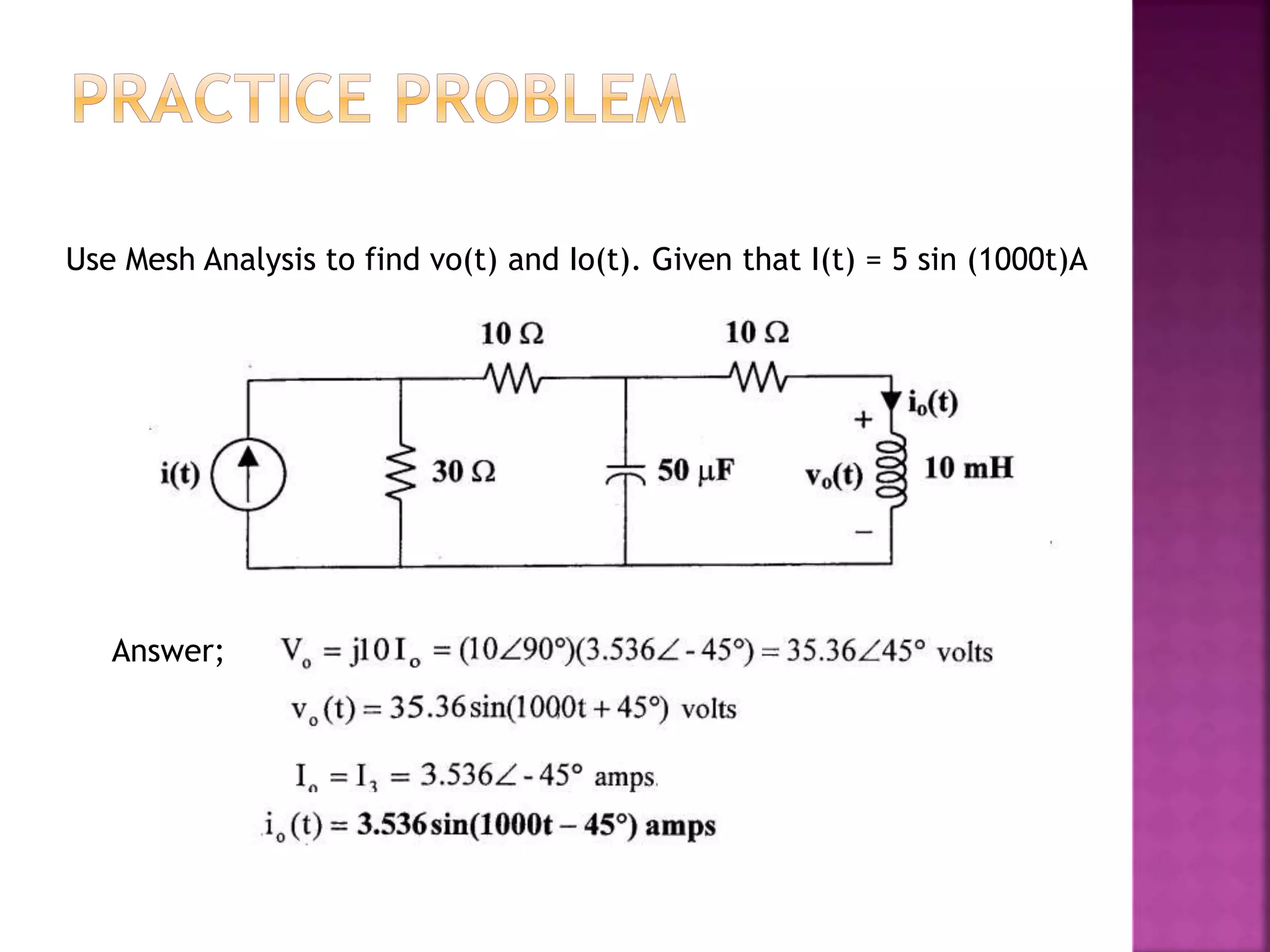
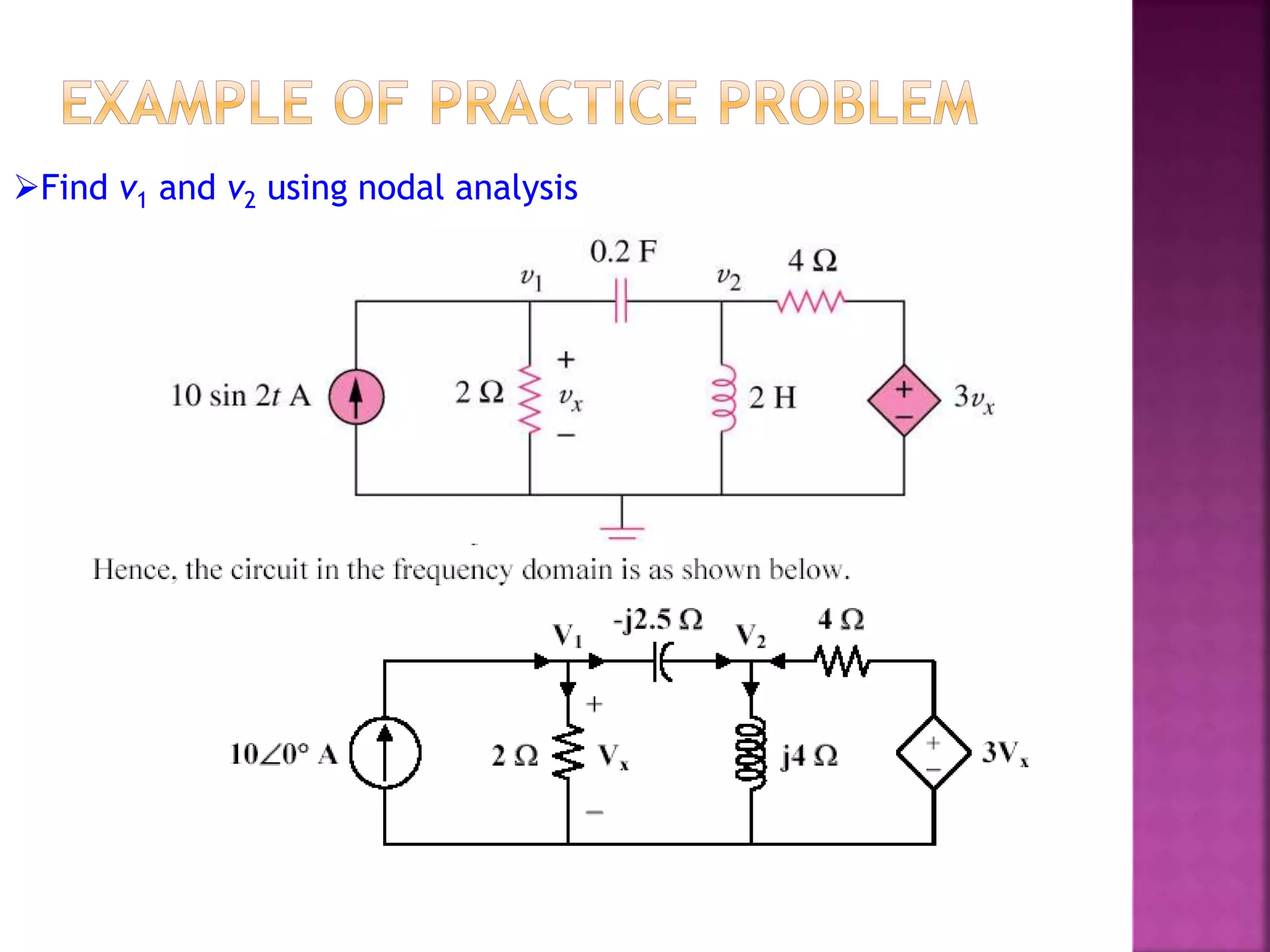
1) The document discusses various circuit analysis techniques for AC circuits including mesh analysis, nodal analysis, superposition, Thevenin's theorem, and Norton's theorem. 2) The key steps for analyzing AC circuits are to first transform the circuit to the phasor domain, then solve the circuit using analysis techniques, and finally transform back to the time domain. 3) Examples are provided for applying each analysis technique to solve for unknown voltages and currents in sample circuits.

1. CHAPTER 1 : CIRCUIT THEORY ANALYSIS
OF AC CIRCUIT

2. 1. Transform the circuit to the Phasor or frequency
domain.
2. Solve the problem using circuit techniques (nodal
analysis, mesh analysis, superposition, etc.).
3. Transform the resulting phasor to the time domain.
Time to Freq Solve
variables in Freq
Freq to Time
NEB 20105 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT

3.  Mesh Analysis using the values of the current
within a certain part of the circuit (need to
draw mesh current)
 Mesh currents direction must be clockwise.
 Apply KVL

4. • occurs when current source is
contained between two essential
meshes.
• This leads to one equation that
incorporates two mesh currents.
Supermesh
• Dependent source is
current/voltage source that
depends on the voltage or current
of another element in the circuit
• Should be treated like an
independent source.
Dependent
Sources

5. Assign mesh currents
Apply KVL to the meshes
Solve the equations
By using Cramer’s rule

6. Calculate the current Io mesh analysis
(2)
(1)
(3)

7. Substitute eqn (3) into eqn (1) & (2)
(4)
(5)

9. Use Mesh Analysis to find vo(t) and Io(t). Given that I(t) = 5 sin (1000t)A
Answer;

10.  *Don’t forget to consider the 3 steps of
Analyzing the AC Circuit
 Select Reference Node and assign with
voltages such as V1, V2, Va, Vb etc.
 Apply KCL to the nodes
 Solve the equation
 For dependent current sources: Treat each dependent
current source like an independent source when Kirchhoff’s
current law is applied to each defined node.
 However, once the equations are established, substitute
the equation for the controlling quantity to ensure that the
unknowns are limited solely to the chosen nodal voltages.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

11. Find v1 and v2 using nodal analysis

14. Answer;

15. Answer;

16. Find Ix using Nodal Analysis

17. Supernode is where the voltage
source (dependent or independent )
is connected between two non-
reference nodes

18. Determine V1 and V2 by using Nodal Analysis

19.  The superposition theorem eliminates the need for solving
simultaneous linear equations by considering the effect on
each source independently.
 To consider the effects of each source we remove the
remaining sources; by setting the voltage sources to zero
(short-circuit representation) and current sources to zero
(open-circuit representation).
 The current through, or voltage across, a portion of the
network produced by each source is then added
algebraically to find the total solution for current or
voltage.
 The only variation in applying the superposition theorem to
AC networks with independent sources is that we will be
working with impedances and Phasors instead of just
resistors and real numbers.

20.  Turn off all independent sources except one source.
Find the output (voltage/current) due to that active
source. *Dependent sources can’t be removed from the
circuit.
 Repeat step 1 for each of the other independent
sources.
 Find the total contribution by adding algebraically all
the contributions due to the independent sources.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

21. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

22. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

23. Use Superposition’s Theorem to find Io.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

24.  Source transformation is a tool used to
simplify a circuit by replacing a voltage
source in series with a resistor by a current
source in parallel with a resistor or vice
versa.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

25.  Consider the 3 steps of analyzing the AC
Circuit
 Apply conversion & calculate where
appropriate (V or I)
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

26. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

27. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

28. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

29. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
Use the method of source transformation, find Ix.

30. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
Use the concept of Source Transformation, find Vo
Vo =

31.  Thevenin’s Theorem is used to simplify a complicated
circuit and replace them by an equivalent circuit just
consists of voltage source, VTH in series with an
impedance, ZTH
 VTH is the open circuit voltage at the terminals
 ZTH is the input or equivalent impedance at the terminals
when the independent sources are turned off.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

32.  If the network has dependent sources, turn off all
independent sources. Dependent source can’t be turn off
because they are controlled by the circuit variables.
 Apply voltage source, vo at terminals a and b and
determine the resulting current, io at terminals a-b and
find terminal voltage vo.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

33. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
Obtain the Thevenin equivalent at terminal a-b of the circuit.

34. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
84.3j88.29.3068.4
9.3610
27048
6j8
)8(6j
86jZ1 





 


Similarly, the 4 resistance is parallel to j12 reactance,
2.1j6.34.1879.3
6.7165.12
9048
12j4
)4(12j
12j4Z2 




 


The Thevenin impedance is the series combination of Z1 and Z2,
64.2j48.6ZZZ 21Th  

35. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
6j8
75120
I1




12j4
75120
I2




Applying KVL around loop b-c-d-e-a-b
0I)6j(I4V 12Th 




9.3610
165720
6.7165.12
75480
6j8
)9075(720
12j4
75480
I6jI4 12












61.24j93.2886.26j8.6625.2j87.379.201724.394.37  

4.22098.376.13998.37  V

36. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
Find the Thevenin equivalent circuit

905555j)3j4(5)4j2(10VTh 
67.0j4
3
)j6(2
I
V
Z
S
S
Th 



37. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
Find the Thevenin Equivalent Circuit

38.  The theorem states that a linear two terminal circuit can be replaced
by an equivalent circuit consisting of a current source IN in parallel
with an impedance ZN
 IN is the short circuit current through the terminals and ZN is the input
or equivalent impedance at the terminal when the independent
sources are turned off.
 To find ZN in the same way to find ZTh. The Thevenin and Norton
impedances are equal ie. ZN = ZTh
 To find the Norton current IN, the short-circuit current flowing from
terminal a to b need to be determined (a). It is evident that the short-
circuit current is IN (b). This must be the same short-circuit current
from terminal a to b (a), since the two circuit are equivalent ie. IN =
ISC. The Thevenin and Norton equivalent circuits are related as VTh =
ZNIN.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

39.  Dependent and independent sources are
treated the same way as in Thevenin
theorem.
BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

40. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
Use Norton’s Theorem and determine the Norton’s Equivalent

41. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

42. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR

43. BPB 21103 NETWORK ANALYSIS CIRCUIT THEORY ANALYSIS OF AC CIRCUIT NFR
Find the Thevenin and Norton Equivalent Circuit
Answer;