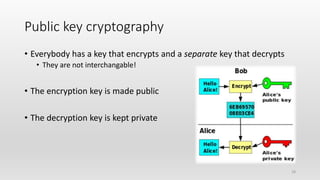
Number theory is a branch of pure mathematics focused on the study of integers, historically known as arithmetic. Key historical figures include the Pythagoreans, Āryabhaṭa, and Diophantus, each contributing foundational concepts such as irrational numbers and polynomial equations. The document also discusses practical applications of number theory in fields like cryptography and error-correcting codes, highlighting its importance in securing digital transactions.

1. Introduction :
Number theory or, in older usage, arithmetic is a branch of
pure mathematics devoted primarily to the study of the
integers. It is sometimes called
"The Queen of Mathematics“.
The older term for number theory is arithmetic. By the early
twentieth century, it had been superseded by "number
theory“ .
The word "arithmetic" is used by the general public to mean
"elementary calculations“ (+, -, *, /).It has also acquired
other meanings in computer science, as floating point
arithmetic.

2. Dawn of arithmetic :
The first historical find of an arithmetical nature is a fragment of a
table: the broken clay tablet Plimpton 322 (Larsa, Mesopotamia, ca.
1800 BCE) contains a list of "Pythagorean triples", i.e., integers such
that . The triples are too many and too large to have been obtained by
brute force. This kind of equation was found…

3. 1800 BCE )

4. More Discoveries :
• Pythagorean mystics gave great importance to the odd and the
even. The discovery that is irrational is credited to the early
Pythagoreans (pre-Theodorus ). By revealing (in modern terms)
that numbers could be irrational, this discovery seems to have
provoked the first foundational crisis in mathematical history; its
proof sometimes credited to Hippasus.
• Āryabhaṭa (476–550 CE) showed that pairs of simultaneous agreement n ≡
a 1 mod m 1 could be solved by a method he called pulveriser; this is a
procedure close to the Euclidean algorithm, which was probably
discovered independently in India. Āryabhaṭa seems to have had in mind
applications to astronomical calculations.

5. Diophantus of Alexandria :
Very little is known about Diophantus of Alexandria.He probably lived
in the third century, that is about 500 years after Euclid. Six out of the
thirteen books of Diophantus's ”Arithmetica” survived in the original
Greek and four more books survived in an Arabic translation.
His book the ”Arithmetica” is a collection of worked-out problems
where the task is to find out rational solutions to a system of polynomial
equations or algebraic equations.

6. 013456…
1
245
Have you ever
thought about why 1
is “one”, 2 is “two”,
3 is “three”…..?
How were they made…???

7.  The numbers we write are made up of algorithms,
(1, 2, 3, 4, etc) called arabic algorithms, to
distinguish them from the roman algorithms (I; II;
III; IV; etc.).
013456…
1
245
Evolution of Number symbols :
The arabs popularise these algorithms, but their origin
goes back to the phenecian merchants that used them to
count and do their commercial contability.

8. 013456…
1
245
Easy, very easy…!
There are
angles !
But what is the actual logic
that exist in the arabic
algorithms?

9. 013456…
1
245
1 angle 2 angles
3 angles 4 angles

10. 013456…
1
245
5 angles 6 angles
7 angles
8 angles

11. 013456…
1
245
9 angles

12. 013456…
1
245
And the most interesting
and intelligent of all…..
Zero Angle !

13. Primes :
A positive integer p greater than 1 is called prime if the
only positive factors of p are 1 and p.
A positive integer that is greater than 1 and is not prime
is called composite.
The fundamental theorem of arithmetic:
Every positive integer can be written uniquely as the
product of primes, where the prime factors are written in
order of increasing size.

14. 14
Primes :
•Examples:
3·5
48 =
100 =
512 =
515 =
28 =
15 =
2·2·2·2·3 = 24·3
2·2·5·5 = 22·52
2·2·2·2·2·2·2·2·2 = 29
5·103
2·2·7

15. Square Roots mod n
• X2 ≡71 (mod 77) has solutions ±15, ±29
• How to (efficiently) solve X2 ≡b (mod pq), where p,q
are (very close) primes?
• Every prime p (except 2) must satisfy p≡1 (mod
4) or p≡3 (mod 4)
• The square roots of 5 mod 11 are ±4

16. Greatest Common Divisor
gcd
• gcd(343, 63)=7, gcd(12345,11111)=1
gcd(1993,3980021)=1993
• Euclidean Algorithm to compute gcd(a,b)
does not require the factorization of the
numbers and is fast.

17. Applications in Real Life
Number theory can be used to find out some of the
important divisibility tests, whether a given integer n is
divisible by an integer m, which are required in various
fields of banking, credit card securities, e – commerce
websites etc. To find out interesting puzzles as various
everyday product identification codes, etc., to get the
knowledge of various bar codes, their combinations,
making of modular designs etc.

18. 18
Public key cryptography
• Everybody has a key that encrypts and a separate key that decrypts
• They are not interchangable!
• The encryption key is made public
• The decryption key is kept private

19. 19
Public key cryptography goals
• Key generation should be relatively easy
• Encryption should be easy
• Decryption should be easy
• With the right key!
• Cracking should be very hard

20. Number Theory for Digital Cash
The whole of encryption works due to number theory. As a result, security
of transactions is ensured. If it were not for number theory, your money
will not be safe in your bank, information about you could be accessed by
anyone.

21. Error-Correcting Code
An error-correcting code is an algorithm for expressing a sequence of numbers such that any
errors which are introduced can be detected and corrected (within certain limitations) based
on the remaining numbers.
Error-correcting codes are also used in CD players, high speed modems, and cellular phones.
Modems use error detection when they compute checksums, which are sums of the digits in a
given transmission modulo some number

22. 22
Encrypting RSA messages
•Formula is c = me mod n

23. 23
Decrypting messages
1. Use the formula m = cd mod n on each number
2. Split the number into individual ASCII character numbers
3. Decode the message into a string

24. 24
Decrypting messages example
• Encrypted message:
• 4501 2867 4894 0361 3630 4496 6720
1. Use the formula m = cd mod n on each number
• 45014669 mod 10379 = 4181
• Etc…
2. Split the numbers into individual characters
• 41 81 02 37 67 88 67 78 75 71 84 85 03 03
3. Decode the message into a string
• Modified ASCII codes:
• 41 81 02 37 67 88 67 78 75 71 84 85 03 03
• Retrieved String is “Go Bangladesh!!”

25. 25
Quantum computers
• A quantum computer could (in principle) factor n in reasonable time
• This would make RSA obsolete!
• Shown (in principle) by Peter Shor in 1993
• You would need a new (quantum) encryption algorithm to encrypt your messages
• This is like saying, “in principle, you could program a computer to correctly
predict the weather”
• A few years ago, IBM created a quantum computer that successfully
factored 15 into 3 and 5
• I bet the NSA is working on such a computer, also