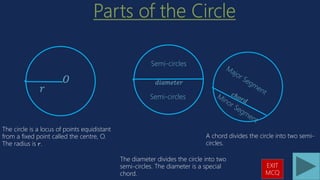
The document contains worked examples and multiple choice practice questions about properties of angles and circles. In the first example, the values of angles QPR and MQO are calculated using properties of isosceles triangles and angles in circles. The following examples involve calculating angle measures using properties such as angles in the same segment being equal, angles at the center being twice the angle at the circumference, and angles formed by tangents and chords.

1. Worked
Examples
Multiple
Choice
Practice
Questions
Lesson
Notes EXIT

2. < 𝑄𝑃𝑅 =
1
2
< 𝑅𝑂𝑄
< 𝑂𝑅𝑄 = 32°
(𝑏𝑎𝑠𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑎𝑛 𝑖𝑠𝑜𝑠𝑐𝑒𝑙𝑒𝑠 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑂𝑄𝑅 𝑎𝑟𝑒 𝑒𝑞𝑢𝑎𝑙)
< 𝑅𝑂𝑄+ < 𝑂𝑅𝑄 +< 𝑂𝑄𝑅 = 180°
(𝑠𝑢𝑚 𝑜𝑓 𝑖𝑛𝑡𝑒𝑟𝑖𝑜𝑟 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑂𝑄𝑅)
< 𝑅𝑂𝑄 + 32° + 32° = 180°
< 𝑅𝑂𝑄 + 64° = 180°
< 𝑅𝑂𝑄 = 180° − 64°
< 𝑅𝑂𝑄 = 116°
∴ < 𝑄𝑃𝑅 =
1
2
116°
∴< 𝑄𝑃𝑅 = 58°
In the diagram, O is the centre of the circle,
< 𝑂𝑄𝑅 = 32° and
< 𝑀𝑃𝑄 = 15°.
Calculate:
i) < 𝑄𝑃𝑅,
ii) < 𝑀𝑄𝑂
𝑊𝐴𝑆𝑆𝐶𝐸 𝐽𝑈𝐿𝑌, 2006.
Show
diagram
More

3. From 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑂𝑀𝑄, < 𝑂𝑀𝑄 +< 𝑀𝑄𝑅 +< 𝑄𝑂𝑀 = 180°
But
< 𝑄𝑂𝑀 = 2 < 𝑄𝑃𝑀, 𝑎𝑛𝑔𝑙𝑒 𝑎𝑡 𝑡ℎ𝑒 𝑐𝑒𝑛𝑡𝑟𝑒 𝑖𝑠 𝑡𝑤𝑖𝑐𝑒 𝑡ℎ𝑒 𝑜𝑛𝑒 𝑜𝑛 𝑡ℎ𝑒
𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒
⇒ < 𝑄𝑂𝑀 = 2 15°
< 𝑄𝑂𝑀 = 30°
⇒< 𝑂𝑀𝑄 +< 𝑀𝑄𝑂 + 30° = 180°
Also, < 𝑂𝑀𝑄 =< 𝑀𝑄𝑂, 𝑏𝑎𝑠𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑖𝑠𝑜𝑠𝑐𝑒𝑙𝑒𝑠 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑂𝑀𝑄
⇒< 𝑂𝑀𝑄 +< 𝑂𝑀𝑄 + 30° = 180°
2 < 𝑂𝑀𝑄 + 30° = 180°
2 < 𝑂𝑀𝑄 = 180° − 30°
2 < 𝑂𝑀𝑄 = 150°
< 𝑂𝑀𝑄 =
150°
2
∴ < 𝑂𝑀𝑄 = 75°
In the diagram, O is the centre of the circle,
< 𝑂𝑄𝑅 = 32° and
< 𝑀𝑃𝑄 = 15°.
Calculate:
i) < 𝑄𝑃𝑅,
ii) < 𝑀𝑄𝑂
𝑊𝐴𝑆𝑆𝐶𝐸 𝐽𝑈𝐿𝑌, 2006.
Show
diagram
Flip to see ii
Worked
Example 2

4. From 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑂𝑀𝑄, < 𝑂𝑀𝑄 +< 𝑀𝑄𝑅 +< 𝑄𝑂𝑀 = 180°
But
< 𝑄𝑂𝑀 = 2 < 𝑄𝑃𝑀, 𝑎𝑛𝑔𝑙𝑒 𝑎𝑡 𝑡ℎ𝑒 𝑐𝑒𝑛𝑡𝑟𝑒 𝑖𝑠 𝑡𝑤𝑖𝑐𝑒 𝑡ℎ𝑒 𝑜𝑛𝑒 𝑜𝑛 𝑡ℎ𝑒
𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒
⇒ < 𝑄𝑂𝑀 = 2 15°
< 𝑄𝑂𝑀 = 30°
⇒< 𝑂𝑀𝑄 +< 𝑀𝑄𝑂 + 30° = 180°
Also, < 𝑂𝑀𝑄 =< 𝑀𝑄𝑂, 𝑏𝑎𝑠𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑖𝑠𝑜𝑠𝑐𝑒𝑙𝑒𝑠 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑂𝑀𝑄
⇒< 𝑂𝑀𝑄 +< 𝑂𝑀𝑄 + 30° = 180°
2 < 𝑂𝑀𝑄 + 30° = 180°
2 < 𝑂𝑀𝑄 = 180° − 30°
2 < 𝑂𝑀𝑄 = 150°
< 𝑂𝑀𝑄 =
150°
2
∴ < 𝑂𝑀𝑄 = 75°
In the diagram, 𝑂 is the centre of the
circle PQRS and < 𝑃𝑄𝑅 = 65°. Find the
value of angle 𝑥.
𝑊𝐴𝑆𝑆𝐶𝐸 𝐽𝑈NE, 2012.
Show
diagram

5. Find the value of a in the diagram below, if AB
and BC are tangents, and O is the centre of the
circle.
A . 74°
B .64°
C . 104°
D .174°
E.124°
EXIT
MCQ

6. In the diagram below, O is the centre of the
circle and AB is a tangent to the circle at A.
Calculate the value of a and b.
B .𝑎 = 90°, 𝑏 = 65°
A .𝑎 = 155°, 𝑏 = 90°
C 𝑎 = 65°, 𝑏 = 90°
D .𝑎 = 90°, 𝑏 = 75°
E .𝑎 = 90°, 𝑏 = 85°
EXIT
MCQ

7. In the diagram below, P, Q, R and S are four points on a
circle. PR and QS intersect at T, such that
<STR=140° and <PRQ=30°. Find <SPR.
B 110°
A . 280°
C .90°
D .70°
•
•°
E .40°
EXIT
MCQ

8. The diagram shows a circle centre O. A, B and C are
points on the circumference. DBO is a straight line. DA
is a tangent to the circle. Calculate < 𝐵𝐶𝐴.
E .124°
A .64°
D .62°
B .14°
C .31°
EXIT
MCQ

9. The diagram shows a circle centre O. A, B and C are
points on the circumference. DBO is a straight line. DA
is a tangent to the circle. Calculate < 𝐴𝑂𝐷.
D.62°
A .64°
E .124°
B .14°
C .31°
EXIT
MCQ

10. The diagram shows a circle centre O. A, B and C are points on
the circumference. DBO is a straight line. DA is a tangent to
the circle at A and < 𝐵𝐴𝐷 = 38°. Find the value of 𝑧.
C .76°
A .38°
D .104°
B .52°
E .164° EXIT
MCQ

11. The diagram shows a circle centre O. A, B and C are points on
the circumference. DBO is a straight line. DA is a tangent to
the circle at A and < 𝐵𝐴𝐷 = 38°. Which theorem can be used to
find 𝑧?
A . Angles in alternate
segment
C . Alternate angles
D . Angles in the same
segment
B . Cyclic quadrilaterals
E . Angles about the centre
EXIT
MCQ

12. The diagram shows a circle centre O. A, B and C are points on
the circumference. DBO is a straight line. DA is a tangent to
the circle at A and < 𝐵𝐴𝐷 = 38°. Find the value of 𝑥.
B .52°
A .38°
D .104°
C .76°
E .164° EXIT
MCQ

13. The diagram shows a circle centre O. A, B and C are points on
the circumference. DBO is a straight line. DA is a tangent to
the circle at A and < 𝐵𝐴𝐷 = 38°. Find the value of 𝑤 − 𝑦.
D .270°
A .38°
B .90°
C .60°
E .180°
EXIT
MCQ

14. In the diagram, O is the centre of the circle. BD and CD
are tangents. Which of the following statements is NOT
true about the diagram?
D .< 𝑂𝐵𝐷 =< 𝑂𝐸𝐵
A .< 𝑂𝐵𝐷+ < 𝑂𝐶𝐷 = 180°
C .< 𝐶𝑂𝐵+ < 𝐵𝐷𝐶 = 180°
B .< 𝑂𝐵𝐸 =< 𝑂𝐸𝐷
C . < 𝑂𝐵𝐷 =< 𝑂𝐶𝐷

15. Semi-circles
Semi-circles
𝑟
𝑂 𝑑𝑖𝑎𝑚𝑒𝑡𝑒𝑟
The circle is a locus of points equidistant
from a fixed point called the centre, O.
The radius is 𝑟.
The diameter divides the circle into two
semi-circles. The diameter is a special
chord.
A chord divides the circle into two semi-
circles.
EXIT
MCQ

16. The tangent to a circle meets the radius at an angle
of 90°. The same thing applies to the diameter
EXIT
MCQ

17. The angle between a chord and a tangent is equal to the
angle created in the alternate segment
EXIT
MCQ

18. Angle 𝑎 and 𝑏 are equal because they are all created in the same
Segment by the same arc or chord
EXIT
MCQ

19. Angle at the centre
𝜃
The angle subtended at the centre is twice the one
subtended at the circumference by an arc.
𝑂
EXIT
MCQ

20. A quadrilateral that has its four vertices on the circumference of a circle is calle
a cyclic quadrilateral
The opposite angles of a cyclic quadrilateral will always sum up to 180°