The document is a lecture on trigonometric functions from a mathematics learning center. It covers the definitions of six circular functions, their properties, and the relationships between them using the unit circle. Additionally, it discusses the signs of these functions in different quadrants, specific values, and the periodic nature of the trigonometric functions.

![youtube.com/@MathematicsOnlineLectures
TRIGONOMETRIC (OR CIRCULAR) FUNCTIONS
Let 𝐗′
𝑶𝐗 and 𝒀𝑶𝒀′ be the coordinate axes. Taking 𝑶 as the centre and a unit radius,
draw a circle, cutting the coordinate axes at 𝑨, 𝑩, 𝑨′
and 𝑩′
, as shown in the figure.
Suppose that a moving point starts from 𝑨 and moves along the circumference of the
circle in an anticlockwise direction. Let it cover an arc length 𝜽 and take the final
position 𝑷(𝒙, 𝒚) .
Join 𝑶𝑷.
Then, ∠𝑨𝑶𝑷 = 𝜽
[⋅.⋅ ∠𝑨𝑶𝑷 =
𝐚𝐫𝐜𝑨𝑷
𝐫𝐚𝐝𝐢𝐮𝐬𝑶𝑷
=
𝜽
𝟏
= 𝜽𝒄
, using 𝜽 =
𝒍
𝒓
].
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-2-320.jpg)
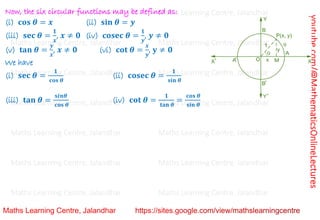



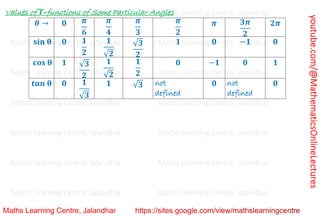
![youtube.com/@MathematicsOnlineLectures
Domain and Range of Trigonometric Functions
The domain and range of each one of the six trigonometric functions is given below.
𝐓‐function Domain Range
𝐬𝐢𝐧 𝒙 𝑹 [−𝟏, 𝟏]
𝐜𝐨𝐬 𝒙 𝑹 [−𝟏, 𝟏]
𝐭𝐚𝐧 𝒙
{𝒙 ∈ 𝑹 ∶ 𝒙 ≠
(𝟐𝐧 + 𝟏)𝝅
𝟐
, 𝒏 ∈ 𝑰}
𝑹
𝐜𝐨𝐭 𝒙 {𝒙 ∈ 𝑹: 𝒙 ≠ 𝒏𝝅, 𝒏 ∈ 𝑰} 𝑹
𝐜𝐨𝐬𝐞𝐜 𝒙 {𝒙 ∈ 𝑹: 𝒙 ≠ 𝒏𝝅, 𝒏 ∈ 𝑰} 𝑹−] − 𝟏, 𝟏[
𝐬𝐞𝐜 𝒙
{𝒙 ∈ 𝑹 ∶ 𝒙 ≠
(𝟐𝐧 + 𝟏)𝝅
𝟐
, 𝒏 ∈ 𝑰}
𝑹−] − 𝟏, 𝟏[
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-8-320.jpg)





![youtube.com/@MathematicsOnlineLectures
Find the value of
(i) 𝐬𝐢𝐧 (
𝟐𝟓𝝅
𝟑
) = 𝐬𝐢𝐧 (𝟖𝝅 +
𝝅
𝟑
) = 𝐬𝒊𝐧
𝝅
𝟑
[ 𝐬𝒊𝐧(𝟐𝒏𝝅 + 𝜽) = 𝐬𝐢𝐧 𝜽]=
√𝟑
𝟐
.
(ii) 𝐜𝐨𝐬 (
𝟒𝟏𝝅
𝟒
) = 𝐜𝐨𝐬 (𝟏𝟎𝝅 +
𝝅
𝟒
) = 𝐜𝐨𝐬
𝝅
𝟒
[ 𝐜𝐨𝐬 (𝟐𝒏𝝅 + 𝜽) = 𝐜𝐨𝐬 𝜽] =
𝟏
√𝟐
.
(iii) 𝐭𝐚𝐧 (−
𝟏𝟔𝝅
𝟑
) = − 𝐭𝐚𝐧
𝟏𝟔𝝅
𝟑
[ 𝐭𝐚𝐧 (−𝜽) = − 𝐭𝐚𝐧 𝜽] = − 𝐭𝐚𝐧 (𝟓𝝅 +
𝝅
𝟑
)
= − 𝐭𝐚𝐧
𝝅
𝟑
[ 𝐭𝐚𝐧 (𝒏𝝅 + 𝜽) = 𝐭𝐚𝐧 𝜽] = −√𝟑.
(iv) 𝐜𝐨𝐭 (
𝟐𝟗𝝅
𝟒
) = 𝐜𝐨𝐭 (𝟕𝝅 +
𝝅
𝟒
) = 𝐜𝐨𝐭
𝝅
𝟒
[ 𝐜𝐨𝐭 (𝒏𝝅 + 𝜽) = 𝐜𝐨𝐭 𝜽] = 𝟏.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-14-320.jpg)
![youtube.com/@MathematicsOnlineLectures
(v) 𝐬𝐞𝐜 (−
𝟏𝟗𝝅
𝟑
) = 𝐬𝐞𝐜 (
𝟏𝟗𝝅
𝟑
) [.⋅ 𝐬𝐞𝐜 (−𝜽) = 𝐬𝐞𝐜 𝜽] = 𝐬𝐞𝐜 (𝟔𝝅 +
𝝅
𝟑
) =
𝐬𝐞𝐜 (
𝝅
𝟑
) [ 𝐬𝐞𝐜 (𝟐𝒏𝝅 + 𝜽) = 𝐬𝐞𝐜 𝜽] = 𝟐.
(vi) 𝐜𝐨𝐬𝐞𝐜 (
−𝟑𝟑𝝅
𝟒
) = − 𝐜𝐨𝐬𝐞𝐜
𝟑𝟑𝝅
𝟒
[.⋅ 𝐜𝐨𝐬𝐞𝐜 (−𝜽) = − 𝐜𝐨𝐬𝐞𝐜 𝜽]
= − 𝐜𝐨𝐬𝐞𝐜 (𝟖𝝅 +
𝝅
𝟒
) = − 𝐜𝐨𝐬𝐞𝐜
𝝅
𝟒
[ 𝐜𝐨𝐬𝐞𝐜 (𝟐𝒏𝝅 + 𝜽) = 𝐜𝐨𝐬𝐞𝐜 𝜽] = −√𝟐.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-15-320.jpg)
![youtube.com/@MathematicsOnlineLectures
Find the value of (i) 𝐬𝐢𝐧 (𝟕𝟔𝟓∘) (ii) 𝐜𝐨𝐬𝐞𝐜 (−𝟏𝟏𝟏𝟎∘) (iii) 𝐜𝐨𝐭 (−𝟔𝟎𝟎∘)
(i) 𝟏𝟖𝟎∘
= 𝝅𝐜
⇒ 𝟕𝟔𝟓∘
= (
𝝅
𝟏𝟖𝟎
× 𝟕𝟔𝟓)
𝐜
= (
𝟏𝟕𝝅
𝟒
)
𝐜
𝐬𝐢𝐧 (𝟕𝟔𝟓∘) = 𝐬𝒊𝒏 (
𝟏𝟕𝝅
𝟒
) = 𝐬𝐢𝐧 (𝟒𝝅 +
𝝅
𝟒
) = 𝐬𝐢𝐧
𝝅
𝟒
[ 𝐬𝐢𝐧 (𝟐𝒏𝝅 + 𝜽) = 𝐬𝐢𝐧 𝛉] =
𝟏
√𝟐
.
(ii) 𝟏𝟖𝟎∘
= 𝝅𝐜
⇒ (𝟏𝟏𝟏𝟎) ∘
= (
𝝅
𝟏𝟖𝟎
× 𝟏𝟏𝟏𝟎)
𝐜
= (
𝟑𝟕𝝅
𝟔
)
𝐜
𝐜𝐨𝐬𝐞𝐜 (−𝟏𝟏𝟏𝟎∘) = − 𝐜𝐨𝐬𝐞𝐜 (𝟏𝟏𝟏𝟎∘) [ 𝐜𝐨𝐬𝐞𝐜 (−𝜽) = − 𝐜𝐨𝐬𝐞𝐜 𝜽] = − 𝐜𝐨𝐬𝐞𝐜 (
𝟑𝟕𝝅
𝟔
)
= − 𝐜𝐨𝐬𝐞𝐜 (𝟔𝝅 +
𝝅
𝟔
) = − 𝐜𝐨𝐬𝐞𝐜
𝝅
𝟔
[ 𝐜𝐨𝐬𝐞𝐜 (𝟐𝒏𝝅 + 𝜽) = 𝐜𝐨𝐬𝐞𝐜 𝜽] = −𝟐.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-16-320.jpg)
![youtube.com/@MathematicsOnlineLectures
(iii) 𝟏𝟖𝟎∘
= 𝝅𝐜
⇒ 𝟔𝟎𝟎∘
= (
𝝅
𝟏𝟖𝟎
× 𝟔𝟎𝟎)
𝐜
= (
𝟏𝟎𝝅
𝟑
)
𝐜
𝐜𝐨𝐭 (−𝟔𝟎𝟎∘) = − 𝐜𝐨𝐭 𝟔𝟎𝟎∘ [ 𝐜𝐨𝐭 (−𝜽) = − 𝐜𝐨𝐭 𝜽] = − 𝐜𝐨𝐭 (
𝟏𝟎𝝅
𝟑
)
= − 𝐜𝐨𝐭 (𝟑𝝅 +
𝝅
𝟑
) = − 𝐜𝐨𝐭
𝝅
𝟑
= −
𝟏
√𝟑
. [ 𝐜𝐨𝐭 (𝒏𝝅 + 𝜽) = 𝐜𝐨𝐭 𝜽]
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-17-320.jpg)
![youtube.com/@MathematicsOnlineLectures
Find the value of
(i) 𝐜𝐨𝐬 𝟏𝟓𝝅 = 𝐜𝐨𝐬 (𝟏𝟒𝝅 + 𝝅) = 𝐜𝐨𝐬 𝝅 [ 𝐜𝐨𝐬 (𝟐𝒏𝝅 + 𝜽) = 𝐜𝐨𝐬 𝜽] = −𝟏.
(ii) 𝐬𝐢𝐧 𝟏𝟔𝝅 = 𝐬𝐦
̇ (𝟏𝟔𝝅 + 𝟎) = 𝐬𝐢𝐧 𝟎∘ [ 𝐬𝐢𝐧 (𝟐𝒏𝝅 + 𝜽) = 𝐬𝐢𝐧 𝜽] = 𝟎.
(iii) 𝐜𝐨𝐬 (−𝝅) = 𝐜𝐨𝐬 𝝅 [ 𝐜𝐨𝐬 (−𝜽) = 𝐜𝐨𝐬 𝜽] = −𝟏.
(iv) 𝐬𝐢𝐧 𝟓𝝅 = 𝐬𝐢𝐧 (𝟒𝝅 + 𝝅) = 𝐬𝐢𝐧𝝅 [ 𝐬𝐢𝐧(𝟐𝒏𝝅 + 𝜽) = 𝐬𝐢𝐧 𝜽]= 𝟎.
(v) 𝐭𝐚𝐧
𝟓𝝅
𝟒
= 𝐭𝐚𝐧 (𝝅 +
𝝅
𝟒
) = 𝐭𝐚𝐧
𝝅
𝟒
[ 𝐭𝐚𝐧 (𝒏𝝅 + 𝜽) = 𝐭𝐚𝐧 𝜽] = 𝟏.
(vi) 𝐬𝐞𝐜 𝟔𝝅 = 𝐬𝐞𝐜 (𝟔𝝅 + 𝟎) = 𝐬𝐞𝐜 𝟎∘ [ 𝐬𝐞𝐜 (𝟐𝒏𝝅 + 𝜽) = 𝐬𝐞𝐜 𝜽] = 𝟏.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-18-320.jpg)
![youtube.com/@MathematicsOnlineLectures
Prove that 𝐬𝐢𝐧𝟐 𝝅
𝟔
+ 𝐜𝐨𝐬𝟐 𝝅
𝟑
—𝒕𝒂𝒏𝟐 𝝅
𝟒
= −
𝟏
𝟐
.
LHS = 𝐬𝐢𝐧𝟐 𝝅
𝟔
+ 𝐜𝐨𝐬𝟐 𝝅
𝟑
—𝒕𝒂𝒏𝟐 𝝅
𝟒
= (
𝟏
𝟐
)
𝟐
+ (
𝟏
𝟐
)
𝟐
− 𝟏𝟐
[⋅.⋅ 𝐬i𝐧
𝝅
𝟔
=
𝟏
𝟐
, 𝐜𝐨𝐬
𝝅
𝟑
=
𝟏
𝟐
and 𝐭𝐚𝐧
𝝅
𝟒
= 𝟏]
= (
𝟏
𝟒
+
𝟏
𝟒
− 𝟏) = −
𝟏
𝟐
= 𝐑𝐇𝐒.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture2-230616085355-596c6113/85/Class-11_Chapter-3_Lecture_2-19-320.jpg)