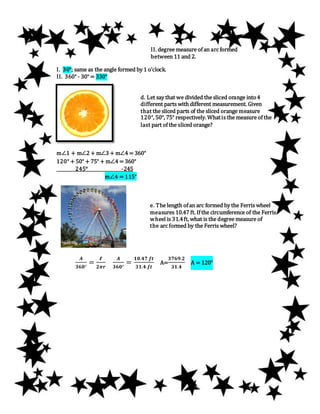
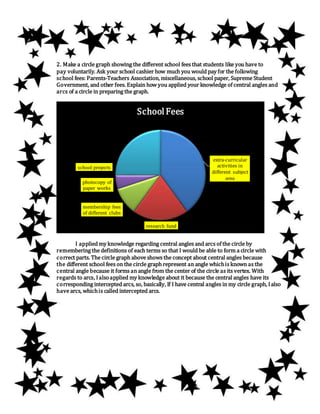
The document describes a student's answers to questions about circles. It includes 5 examples of real-world situations involving circles and formulates problems about them. The student then creates a circle graph showing school fees and uses it to formulate 2 additional problems involving arcs, central angles, and sectors of a circle. The problems are then solved using formulas for these circle concepts.

1. Sophia Marie D. Verdeflor Grade 10-1 STE
Activity 13: My Real World
Answer the following. Use the rubric provided to rate your work.
1. Name 5 objects or cite 5 situations in real life where chords, arcs and central angles
of a circle are illustrated. Formulate problems out of these objects or situations,
then solve.
a. Charmaine has a circulargarden that she
separates into five equal parts. If the radius of
the garden is 15 m, what is the length of the
arc of each part?
360÷5=72°
𝐀
𝟑𝟔𝟎°
=
𝓵
𝟐𝛑𝐫
𝟕𝟐°
𝟑𝟔𝟎°
=
𝓵
𝟐𝛑(𝟏𝟓)
𝟏
𝟓
=
𝓵
𝟑𝟎𝛑
𝟑𝟎𝛑
𝟓
= 𝓵 𝓵= 18.84 m
b. The radius of the pizza measures 20 cm. If
the arc of the sliced part of the pizza measures
60°, what is the area of the sector of the pizza?
𝒎𝒆𝒂𝒔𝒖𝒓𝒆 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒓𝒄
𝟑𝟔𝟎°
=
𝟔𝟎°
𝟑𝟔𝟎°
=
𝟏
𝟔
𝑨 = 𝝅𝒓 𝟐
𝑨 = 𝝅(𝟐𝟎𝒄𝒎) 𝟐
𝑨 = 𝟒𝟎𝟎𝝅𝒄𝒎 𝟐
𝟏
𝟔
x (400 𝝅𝒄𝒎 𝟐
) =
𝟒𝟎𝟎𝝅
𝟔
𝒄𝒎 𝟐
=
𝟐𝟎𝟎𝝅
𝟑
𝒄𝒎 𝟐
= 209.44 𝐜𝐦 𝟐
c. The clock stops at exactly 1:00. The long hand
points to12 and the short hand points to1. If the
angle formed by 1 o’clock measures 30°, find the
following:
I. degree measure of an arc formed between
12 and 1

2. II. degree measure of an arc formed
between 11 and 2.
I. 30°; same as the angle formed by 1 o’clock.
II. 360° - 30° = 330°
d. Let say that we divided the sliced orange into4
different parts with different measurement. Given
that the sliced parts of the sliced orange measure
120°, 50°, 75° respectively. Whatis the measure of the
last part of the sliced orange?
m∠1 + m∠2 + m∠3 + m∠4 = 360°
120° + 50° + 75° + m∠4 = 360°
245° -245
m∠4 = 115°
e
e. The length of an arc formed by the Ferris wheel
measures 10.47 ft. If the circumference of the Ferris
wheel is 31.4ft, what is the degree measure of
the arc formed by the Ferris wheel?
𝑨
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅𝒓
𝑨
𝟑𝟔𝟎°
=
𝟏𝟎.𝟒𝟕 𝒇𝒕
𝟑𝟏.𝟒 𝒇𝒕
A=
𝟑𝟕𝟔𝟗.𝟐
𝟑𝟏.𝟒
A = 120°

3. 2. Make a circle graph showing the different school fees that students like you have to
pay voluntarily. Ask your school cashier how much you would pay for the following
school fees: Parents-Teachers Association, miscellaneous, school paper, Supreme Student
Government, and other fees. Explain how you applied your knowledge of central angles and
arcs of a circle in preparing the graph.
I applied my knowledge regarding central angles and arcs of the circle by
remembering the definitions of each terms so that I would be able to form a circle with
correct parts. The circle graph above shows the concept about central angles because
the different school fees on the circle graph represent an angle whichis known as the
central angle because it forms an angle from the center of the circle as its vertex. With
regards to arcs, Ialsoapplied my knowledge about it because the central angles have its
corresponding intercepted arcs, so, basically, If I have central angles in my circle graph, Ialso
have arcs, whichis called intercepted arcs.
extra-curricular
activities in
different subject
area
research fund
membership fees
of different clubs
photocopy of
paper works
school projects
SchoolFees

4. 3. Using the circle graph that you made in number 2, formulate at least twoproblems
involving arcs, central angles, and sectors of a circle, then solve.
The different school fees of a typical and ordinary student like me are represented
in a circle graph above namely:“School Fees”. Let say that Ihave Php 5000 budget
for different school fees for the whole school year. Ispend, Php 2000 for extra-curricular
activities in different subject area, Php 1500 for research fund, Php 500 for
membership fees of different clubs, Php 200 for photocopy of paper works, and Php
800 for school projects.
a. In the circle graph, what is the measure of the central angle corresponding toeach item?
By following the formula: (amount of money per school fees ÷ budget for the
whole school year-Php 5000) x 360
 Extra-curricular activities in different subjectarea
(2000 ÷ 5000) x 360 = 144°
 Researchfund
(1500 ÷ 5000) x 360 = 108°
 Membership fees of different clubs
(500 ÷ 5000) x 360 = 36°
 Photocopy of paper works
(200 ÷ 5000) x 360 = 14°
 School projects
(800 ÷ 5000) x 360 = 58°
b. Suppose the radius of the circle graphis 35 cm. What is the area of each sector in the
circle graph?
 Extra-curricular activities in different subjectarea
𝒎𝒆𝒂𝒔𝒖𝒓𝒆 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒓𝒄
𝟑𝟔𝟎°
=
𝟏𝟒𝟒°
𝟑𝟔𝟎°
= (
𝟐
𝟓
)( 𝟏𝟐𝟐𝟓 𝝅𝒄𝒎 𝟐) =
𝟐𝟒𝟓𝟎 𝝅
𝟓
𝒄𝒎 𝟐
=
𝟕𝟔𝟗𝟑
𝟓
𝒄𝒎 𝟐
=
1538.6 𝒄𝒎 𝟐
 Researchfund
𝒎𝒆𝒂𝒔𝒖𝒓𝒆 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒓𝒄
𝟑𝟔𝟎°
=
𝟏𝟎𝟖°
𝟑𝟔𝟎°
= (
𝟑
𝟏𝟎
) ( 𝟏𝟐𝟐𝟓 𝝅𝒄𝒎 𝟐)=
𝟑𝟔𝟕𝟓 𝝅
𝟏𝟎
𝒄𝒎 𝟐
=
𝟏𝟏𝟓𝟑𝟗.𝟓
𝟏𝟎
𝒄𝒎 𝟐
=
1153.95 𝒄𝒎 𝟐

5.  Membership fees of different clubs
𝒎𝒆𝒂𝒔𝒖𝒓𝒆 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒓𝒄
𝟑𝟔𝟎°
=
𝟑𝟔°
𝟑𝟔𝟎°
= (
𝟏
𝟏𝟎
) ( 𝟏𝟐𝟐𝟓 𝝅𝒄𝒎 𝟐)=
𝟏𝟐𝟐𝟓 𝝅
𝟏𝟎
𝒄𝒎 𝟐
=
𝟑𝟖𝟒𝟔.𝟓
𝟏𝟎
𝒄𝒎 𝟐
=
384.65 𝒄𝒎 𝟐
 Photocopy of paper works
𝒎𝒆𝒂𝒔𝒖𝒓𝒆 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒓𝒄
𝟑𝟔𝟎°
=
𝟏𝟒°
𝟑𝟔𝟎°
= (
𝟕
𝟏𝟖𝟎
) ( 𝟏𝟐𝟐𝟓 𝝅𝒄𝒎 𝟐)=
𝟖𝟓𝟕𝟓 𝝅
𝟏𝟖𝟎
𝒄𝒎 𝟐
=
𝟐𝟔𝟗𝟐𝟓.𝟓
𝟏𝟖𝟎
𝒄𝒎 𝟐
=
149.58611 𝒄𝒎 𝟐
 School projects
𝒎𝒆𝒂𝒔𝒖𝒓𝒆 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒓𝒄
𝟑𝟔𝟎°
=
𝟓𝟖°
𝟑𝟔𝟎°
= (
𝟐𝟗
𝟏𝟖𝟎
)( 𝟏𝟐𝟐𝟓 𝝅𝒄𝒎 𝟐)=
𝟑𝟓𝟓𝟐𝟓 𝝅
𝟏𝟖𝟎
𝒄𝒎 𝟐
=
𝟏𝟏𝟏𝟓𝟒𝟖.𝟓
𝟏𝟖𝟎
𝒄𝒎 𝟐
=
619.71388 𝒄𝒎 𝟐
c. With the same value of the radius, how about the measure of the length of the arc of
each sector?
 Extra-curricular activities
𝑨
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅𝒓
𝟏𝟒𝟒°
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅(𝟑𝟓)
𝟐
𝟓
=
𝓵
𝟕𝟎𝝅
𝟏𝟒𝟎𝝅
𝟓
= 𝓵
𝟒𝟑𝟗.𝟔
𝟓
= 𝓵 𝓵=87.92
 Researchfund
𝑨
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅𝒓
𝟏𝟎𝟖°
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅(𝟑𝟓)
𝟑
𝟏𝟎
=
𝓵
𝟕𝟎𝝅
𝟐𝟏𝟎𝝅
𝟏𝟎
= 𝓵
𝟔𝟓𝟗.𝟒
𝟏𝟎
= 𝓵 𝓵=65.94
 Membership fees of different clubs
𝑨
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅𝒓
𝟑𝟔°
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅(𝟑𝟓)
𝟏
𝟔
=
𝓵
𝟕𝟎𝝅
𝟕𝟎𝝅
𝟔
= 𝓵
𝟐𝟏𝟗.𝟖
𝟔
= 𝓵 𝓵=36.633
 Photocopy of paper works
𝑨
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅𝒓
𝟏𝟒°
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅(𝟑𝟓)
𝟕
𝟏𝟖𝟎
=
𝓵
𝟕𝟎𝝅
𝟒𝟗𝟎𝝅
𝟏𝟖𝟎
= 𝓵
𝟏𝟓𝟑𝟖.𝟔
𝟏𝟖𝟎
= 𝓵 𝓵=8.548
 School projects
𝑨
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅𝒓
𝟓𝟖°
𝟑𝟔𝟎°
=
𝓵
𝟐𝝅(𝟑𝟓)
𝟐𝟗
𝟏𝟖𝟎
=
𝓵
𝟕𝟎𝝅
𝟐𝟎𝟑𝟎𝝅
𝟏𝟖𝟎
= 𝓵
𝟔𝟑𝟕𝟒.𝟐
𝟏𝟖𝟎
= 𝓵 𝓵=35.412