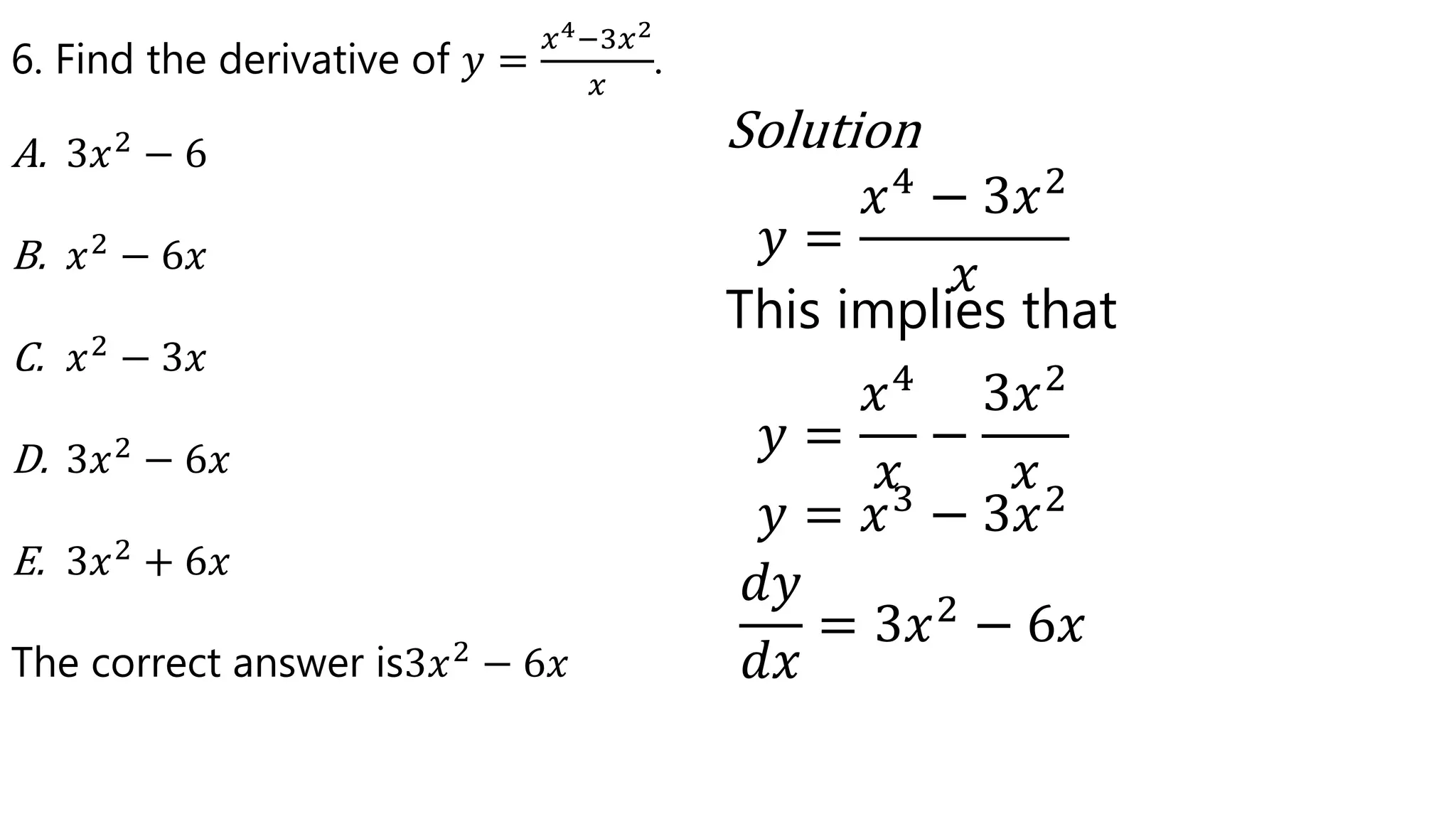- The document discusses differentiation and integration of algebraic functions. - It provides rules for finding the derivatives of functions such as y = xn, y = axn, and the sum or difference of functions. - It also discusses that the derivative of a constant is 0, and provides examples such as dy/dx = 0 for y = 1. - Integration is discussed as the reverse process of differentiation, with rules provided for indefinite integrals of functions like xn and definite integrals over an interval.

1. DIFFERENTIATION OF ALGEBRAIC FUNCTIONS
• 𝑦 = 𝑥 𝑛
• 𝑓 𝑥 = 𝑥 𝑛
• 𝑦 = 𝑥3
• 𝑦 = 𝑥2
• 𝑦 = 𝑥−1
•
𝑑𝑦
𝑑𝑥
= 𝑛𝑥 𝑛−1
• 𝑓′ 𝑥 = 𝑛𝑥 𝑛−1
•
𝑑𝑦
𝑑𝑥
= 3𝑥3−1
•
𝑑𝑦
𝑑𝑥
= 3𝑥2
•
𝑑𝑦
𝑑𝑥
= 2𝑥2−1
•
𝑑𝑦
𝑑𝑥
= 2𝑥1
•
𝑑𝑦
𝑑𝑥
= 2𝑥
•
𝑑𝑦
𝑑𝑥
= −1𝑥−1−1
•
𝑑𝑦
𝑑𝑥
= −1𝑥−2
•
𝑑𝑦
𝑑𝑥
= −
1
𝑥2

2. THE DERIVATIVE OF A CONSTANT
• 𝑦 = 𝑐
• 𝑦 = 𝑐𝑥0
•
𝑑𝑦
𝑑𝑥
= 0𝑐𝑥0−1
•
𝑑𝑦
𝑑𝑥
= 0𝑐𝑥−1
•
𝑑𝑦
𝑑𝑥
=0
• 𝑦 = 1,
𝑑𝑦
𝑑𝑥
= 0
• 𝑦 = −1,
𝑑𝑦
𝑑𝑥
= 0
• 𝑦 = 59,
𝑑𝑦
𝑑𝑥
= 0
• 𝑦 = 94,
𝑑𝑦
𝑑𝑥
= 0

3. DIFFERENTIATION OF ALGEBRAIC FUNCTIONS
• 𝑦 = 𝑎𝑥 𝑛
•
𝑑𝑦
𝑑𝑥
= 2(6)𝑥2−1
•
𝑑𝑦
𝑑𝑥
= 12𝑥1
•
𝑑𝑦
𝑑𝑥
= 12𝑥
• 𝑦 = 6𝑥2
,

4. DIFFERENTIATION (TERM-BY-TERM)
• 𝑦 = 𝑥3
− 3𝑥5
+ 3
•
𝑑𝑦
𝑑𝑥
= 3𝑥2
− 15𝑥4

5. INTEGRATION OF SIMPLE ALGEBRAIC FUNCTIONS
The reverse of differentiation
𝑦 = 𝑥2 + 𝐶
𝑑𝑦
𝑑𝑥
= 2𝑥
2𝑥 𝑑𝑥
= 𝑥2 + 𝐶
Constant of integrationIndefinite integral

6. INTEGRATION OF SIMPLE ALGEBRAIC FUNCTIONS
The reverse of differentiation
𝑥 𝑛 𝑑𝑥 =
𝑥 𝑛+1
𝑛 + 1
+ 𝐶

7. INTEGRATION OF SIMPLE ALGEBRAIC FUNCTIONS
The definite integral
𝑎
𝑏
𝑥 𝑛 𝑑𝑥 =
𝑥 𝑛+1
𝑛 + 1
|
𝑏
𝑎
=
𝑏 𝑛+1
𝑛 + 1
−
𝑎 𝑛+1
𝑛 + 1

8. DIFFERENTIATION
𝑓𝑖𝑛𝑑 𝑡ℎ𝑒 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 … .
𝑓𝑖𝑛𝑑
𝑑𝑦
𝑑𝑥
𝑜𝑓 𝑦 = ⋯ .
𝑓𝑖𝑛𝑑 𝑓′
𝑥 𝑜𝑓 𝑓 𝑥 = ⋯
𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒 𝑡ℎ𝑒 𝑟𝑎𝑡𝑒 𝑜𝑓 𝑐ℎ𝑎𝑛𝑔𝑒 𝑜𝑓 𝑦 =
⋯ .
𝑓𝑖𝑛𝑑 𝑡ℎ𝑒 𝑔𝑟𝑎𝑑𝑖𝑒𝑛𝑡 𝑜𝑓 𝑦 = ⋯ . .

9. WASSCE Nov/Dec 2018
Solution
1
3
3 + 𝑥3
+ 2𝑥4
𝑥2 𝑑𝑥
We simplify the function first, by splitting the
numerators,
1
3
3 + 𝑥3
+ 2𝑥4
𝑥2
𝑑𝑥 =
1
3
3
𝑥2
+
𝑥3
𝑥2
+
2𝑥4
𝑥2
𝑑𝑥
We now simplify and apply the laws of indices
1
3
3𝑥−2
+ 𝑥 + 2𝑥2
𝑑𝑥
We now integrate to obtain,
=
3𝑥−2+1
−2 + 1
+
1 × 𝑥1+1
1 + 1
+
2𝑥2+1
2 + 1
|
3
1
=
3𝑥−1
−1
+
𝑥2
2
+
2𝑥3
3
|
3
1
= −3𝑥−1 +
1
2
𝑥2 +
2𝑥3
3
|
3
1
= −
3
𝑥
+
1
2
𝑥2
+
2𝑥3
3
|
3
1
= −
3
3
+
32
2
+
2 33
3
− −
3
1
+
12
2
+
2 13
3
=
70
3
Evaluate 1
3 3+𝑥3+2𝑥4
𝑥2 𝑑𝑥

10. JAMB 2000 Solution
𝐴𝑐𝑐𝑜𝑟𝑑𝑖𝑛𝑔 𝑡𝑜 𝑡ℎ𝑒 𝑞𝑢𝑒𝑠𝑡𝑖𝑜𝑛,
𝑑𝑦
𝑑𝑥
= 3𝑥 + 2
Integrating both sides ,
𝑦 = 3𝑥 + 2 𝑑𝑥
𝑦 =
3𝑥2
2
+ 2𝑥 + 𝑐
The curve passes through 0,0 ,
0 =
3
2
0 2 + 2 0 + 𝑐
𝑐 = 0
∴ 𝑦 =
3
2
𝑥2 + 2𝑥
A function 𝑓(𝑥) passes through the origin and its first
derivative is 3𝑥 + 2. what is 𝑓(𝑥)
A. 𝑦 =
3
2
𝑥2 + 2𝑥
B. B. 𝑦 =
3
2
𝑥2
+ 𝑥
C. C. 𝑦 = 3 𝑥2
+
𝑥
2
D. 𝑦 = 3 𝑥2
+ 2𝑥

11. JAMB 2004 Solution
𝑦 = (2 + 3𝑥)(1 − 𝑥)
→ 𝑦 = 2 − 2𝑥 + 3𝑥 − 3𝑥2
𝑦 = 2 + 𝑥 − 3𝑥2
𝑑𝑦
𝑑𝑥
= 1 − 6𝑥
Find the derivative of (2 + 3𝑥)(1 − 𝑥) with respect to x

12. WASSCE May/June
2018, (Elective )
Evaluate
1
2
1
𝑥3 − 4
𝑥3
𝑑𝑥
Solution
1
2
1
𝑥3
− 4
𝑥3
𝑑𝑥
Splitting the numerator,
1
2
1
𝑥3
𝑥3
−
4
𝑥3
𝑑𝑥
1
2
1
1 − 4𝑥−3 𝑑𝑥
𝑥 −
4𝑥−3+1
−3 + 1
1
1
2
𝑥 +
2
𝑥2
1
1
2
𝑥 +
2
𝑥2
1
1
2
= 1 +
2
12
−
1
2
−
2
1
2
2 = −5.5

13. 1. Given that 𝑦 = 3𝑥2 − 𝑥3, find
𝑑𝑦
𝑑𝑥
.
A. 6𝑥 − 3𝑥4
B. 6𝑥 − 3
C. 3𝑥 − 3𝑥2
D. 6𝑥 − 3𝑥2
E. 6 − 3𝑥2
The correct answer is 6𝑥 − 3𝑥2
Solution
𝑦 = 3𝑥2
− 𝑥3
𝑑𝑦
𝑑𝑥
= 6𝑥 − 3𝑥2

14. 2. Evaluate 0
1
𝑥 + 1 1 − 𝑥 𝑑𝑥
A.
1
3
B. −
1
3
C.
2
3
D. −
2
3
E. 1
The correct answer is
2
3
Solution
0
1
𝑥 + 1 1 − 𝑥 𝑑𝑥
=
0
1
1 − 𝑥2
𝑑𝑥
= 𝑥 −
𝑥3
3
1
0
= 1 −
13
3
− 0 =
2
3

15. 3. Given that 𝑓 𝑥 = 2 −
1
𝑥
2
, find 𝑓′(1).
A. 2
B. 8
C. 4
D. 6
E. 5
The correct answer is 2
Solution
𝑓 𝑥 = 2 −
1
𝑥
2
→ 𝑓 𝑥 = 4 −
4
𝑥
+
1
𝑥2
𝑓 𝑥 = 4 − 4𝑥−1 + 𝑥−2
𝑓′ 𝑥 = 4𝑥−2
−2𝑥−3
𝑓′ 𝑥 =
4
𝑥2
−
2
𝑥3
𝑓′(1) =
4
12
−
2
13
= 2

16. 4. If 𝑓′(𝑥) = 2𝑥 − 1 and f 1 = 2, find 𝑓(𝑥)?
A. 𝑓 𝑥 = 𝑥2 − 𝑥 − 2
B. 𝑓 𝑥 = 𝑥2 + 𝑥 + 2
C. 𝑓 𝑥 = 𝑥2 − 𝑥 + 2
D. 𝑓 𝑥 = 2𝑥2
− 𝑥 + 2
E. 𝑓 𝑥 = 3𝑥2 − 𝑥 + 2
The correct answer is 𝑓 𝑥 = 𝑥2 − 𝑥 + 2
Solution
𝑓′
(𝑥) = 2𝑥 − 1
Integrating both sides with respect to
𝑥
𝑓 𝑥 =
2𝑥2
2
− 𝑥 + 𝑐
𝑓 𝑥 = 𝑥2 − 𝑥 + 𝑐
We were given that 𝑓 1 = 2
2 = 12
− 1 + 𝑐
𝑐 = 2
𝑓 𝑥 = 𝑥2
− 𝑥 + 2

17. 5. Find the gradient of 𝑦 = 2𝑥3 − 𝑥2 − 2𝑥 at 𝑥 = −1
A. 6
B. 8
C. 4
D. 6
E. 5
The correct answer is 6
Solution
𝑦 = 2𝑥3 − 𝑥2 − 2𝑥
𝑑𝑦
𝑑𝑥
= 6𝑥2 − 2𝑥 − 2
𝑑𝑦
𝑑𝑥
= 6 −1 2
− 2 −1 − 2
𝑑𝑦
𝑑𝑥
= 6
⟹ 𝑇ℎ𝑒 𝑔𝑟𝑎𝑑𝑖𝑒𝑛𝑡 𝑜𝑓 𝑦 = 2𝑥3
− 𝑥2
− 2𝑥
is 6

18. 6. Find the derivative of 𝑦 =
𝑥4−3𝑥2
𝑥
.
A. 3𝑥2
− 6
B. 𝑥2 − 6𝑥
C. 𝑥2
− 3𝑥
D. 3𝑥2
− 6𝑥
E. 3𝑥2 + 6𝑥
The correct answer is3𝑥2 − 6𝑥
Solution
𝑦 =
𝑥4
− 3𝑥2
𝑥
This implies that
𝑦 =
𝑥4
𝑥
−
3𝑥2
𝑥
𝑦 = 𝑥3
− 3𝑥2
𝑑𝑦
𝑑𝑥
= 3𝑥2
− 6𝑥

19. 7. The curve 3𝑦 + 2𝑥2 = 6, passes through the point (1,
4
3
). Find the
gradient of the tangent to the curve at this point.
A. −
4
3
B.
4
3
C.
3
4
D. −
3
4
E. 4
Solution
3𝑦 + 2𝑥2
= 6
Making 𝑦 the subject we have;
𝑦 = 2 −
2
3
𝑥2
𝑑𝑦
𝑑𝑥
= −
4
3
𝑥
When 𝑥 = 1
𝑑𝑦
𝑑𝑥
= −
4
3
= 𝑚

20. 8. The curve 3𝑦 + 2𝑥2 = 6, passes through the point (1,
4
3
). Find the
equation of the tangent to the curve at this point.
A. 3𝑦 − 4𝑥 − 8 = 0
B. 3𝑦 + 4𝑥 + 8 = 0
C. 3𝑦 + 4𝑥 − 8 = 0
D. 4𝑦 + 3𝑥 − 8 = 0
E. 4𝑦 − 3𝑥 − 8 = 0
The correct answer is3𝑦 + 4𝑥 − 8 = 0
Solution
3𝑦 + 2𝑥2 = 6
Making 𝑦 the subject we have;
𝑦 = 2 −
2
3
𝑥2
𝑑𝑦
𝑑𝑥
= −
4
3
𝑥
When 𝑥 = 1
𝑑𝑦
𝑑𝑥
= −
4
3
= 𝑚
The equation of the tangent is given by;
𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1)
𝑦 −
4
3
= −
4
3
(𝑥 − 1)
3𝑦 − 4 = −4(𝑥 − 1)
3𝑦 − 4 = −4𝑥 + 4
The equation is;
3𝑦 + 4𝑥 − 8 = 0

21. 9. Evaluate the indefinite integral 3𝑥2 − 4𝑥3 𝑑𝑥
A. 𝑥3
− 𝑥4
B.
𝑥3
3
−
𝑥4
4
+ 𝐶
C. 𝑥3
+ 𝑥4
+ 𝐶
D. 3𝑥3
− 4𝑥4
+ 𝐶
E. 𝑥3
− 𝑥4
+ 𝐶
The correct answer is𝑥3 − 𝑥4 + 𝐶
Solution
3𝑥2
− 4𝑥3
𝑑𝑥
=
3𝑥3
3
−
4𝑥4
4
+ 𝐶
= 𝑥3 − 𝑥4 + 𝐶

22. 10. Evaluate 0
1
3𝑥2 + 4𝑥3 𝑑𝑥
A. −2
B. 2
C. 3
D. 4
E. -3
The correct answer is 2
Solution
0
1
3𝑥2 + 4𝑥3 𝑑𝑥
=
3𝑥3
3
+
4𝑥4
4
1
0
= 𝑥3
+ 𝑥4 1
0
= 13 + 14 − 0 = 2

23. SUMMARY
If we have 𝑦 = 𝑥 𝑛, then
𝑑𝑦
𝑑𝑥
= 𝑛𝑥 𝑛−1
If we have 𝑦 = 𝑥 𝑛, then
𝑥 𝑛 𝑑𝑥 =
1
𝑛 + 1
𝑥 𝑛+1 + 𝐶, 𝑛 ≠ −1
Integration is the reverse of differentiation