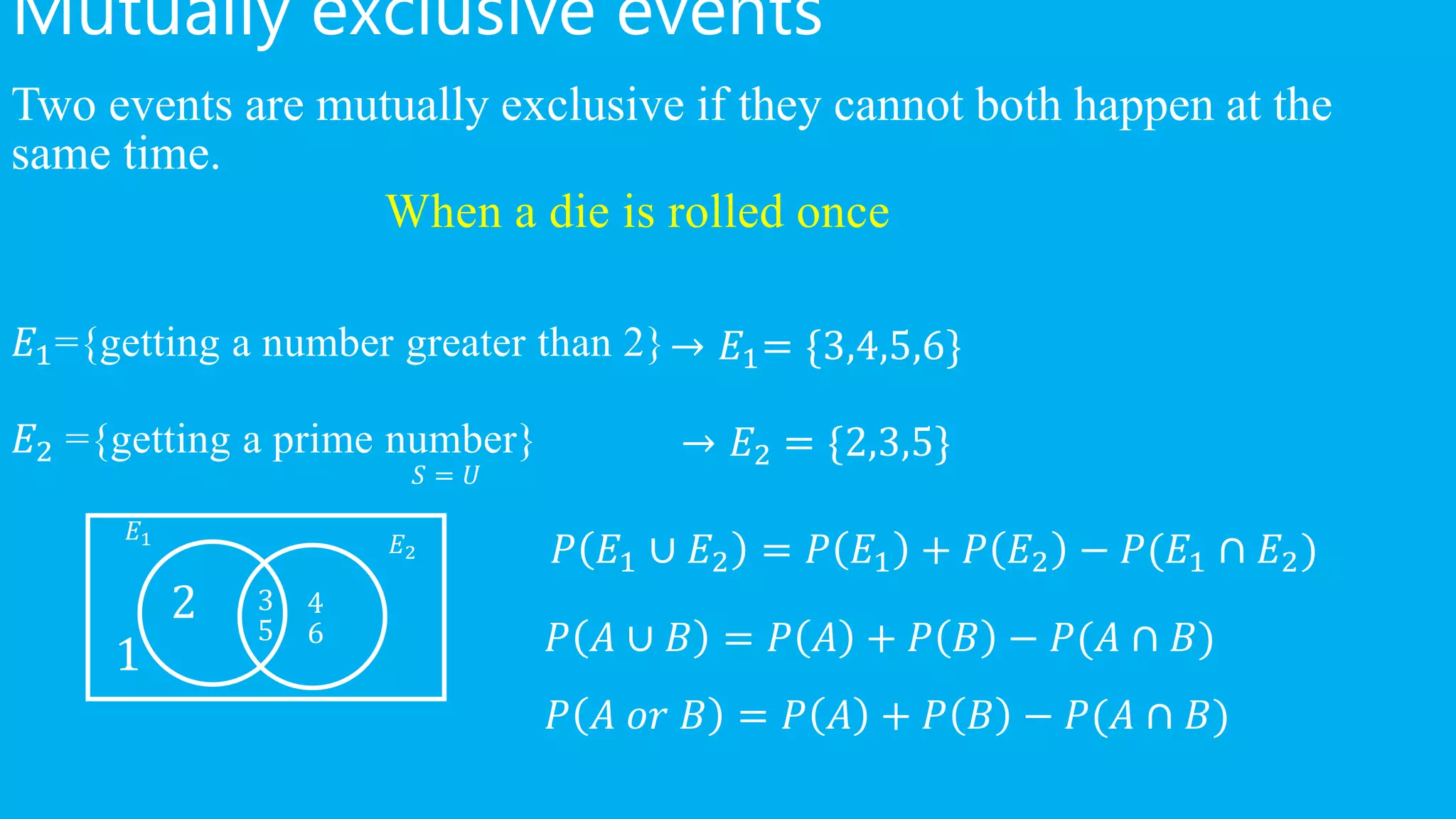This document provides formulas and examples for calculating probabilities of events. It defines mutually exclusive events as events that cannot occur at the same time. It gives the formulas for calculating the probability of the union or intersection of events. Examples include calculating probabilities of rolling dice, picking beads from a bag, and selecting fruits or students at random.

1. 𝑃 𝐸 =
𝑛(𝐸)
𝑛(𝑆)
Computing Probability

2. Mutually exclusive events
Two events are mutually exclusive if they cannot both happen at the
same time.
𝑆 = 𝑈
𝐸1 𝐸2 𝑃 𝐸1 ∪ 𝐸2 = 𝑃 𝐸1 + 𝑃 𝐸2 − 𝑃(𝐸1 ∩ 𝐸2)
When a die is rolled once
𝐸1={getting a number greater than 2}
𝐸2 ={getting a prime number}
→ 𝐸1= {3,4,5,6}
→ 𝐸2 = {2,3,5}
3
5
2 4
6
1
𝑃 𝐴 𝑜𝑟 𝐵 = 𝑃 𝐴 + 𝑃 𝐵 − 𝑃(𝐴 ∩ 𝐵)
𝑃 𝐴 ∪ 𝐵 = 𝑃 𝐴 + 𝑃 𝐵 − 𝑃(𝐴 ∩ 𝐵)

3. Mutually exclusive events
Two events are mutually exclusive if they cannot both happen at the
same time.
𝑆 = 𝑈
A B
𝑃 𝐴 ∪ 𝐵 = 𝑃 𝐴 + 𝑃 𝐵
When a die is rolled once
A={getting a 3}
B = {getting a 4}
𝑃 𝐴𝑜𝑟𝐵 = 𝑃 𝐴 + 𝑃 𝐵

4. Properties of Probability
1. For any event A, 0 ≤ 𝑃(𝐴) ≤ 1
2. 𝑃 ∅ = 0
3. 𝑃 𝑆 = 1
4. The sum of all probabilities of events in the sample space
equals 1

5. The Complement of an event
𝑆 = 𝑈
A
𝐴
If 𝐴 denotes the complement of event A, then 𝑃 𝐴 = 1 −
𝑃(𝐴)

6. The Intersection of two events
If A and B denote two events
𝑃 𝐴 ∩ 𝐵 = 𝑃(𝐴) × 𝑃(𝐵)

7. In a basket, there are
6 grapes, 11 bananas
and 13 oranges. If one
fruit is chosen at
random, what is the
probability that the fruit
is either a grape or a
banana?
JAMB 2007
Solution
Probability of choosing grape =
6
30
Probability of choosing banana =
11
30
Probability of choosing grape or banana
=
6
30
+
11
30
=
17
30

8. A bag contains 6 red,
8 black and 10 yellow
identical beads. Two
beads are picked at
random, one after the
other, without
replacement. Find the
probability that
a. both are red
b. one is black and the
other is yellow
WASSCE May/June 2009
Solution
Total number of beads = 6 + 8 + 10 = 24
P(Red)=
6
24
P(Black)=
8
24
P(Yellow)=
10
24
a. P(both are red)=
6
24
×
5
23
=
5
92
b. P(one is black and the other is yellow)
= P(𝟏 𝒔𝒕 is black and 2 𝑛𝑑 is yellow) or P(𝟏 𝒔𝒕 is
yellow and 2 𝑛𝑑 is black)
=
8
24
×
10
23
+
10
24
×
8
24
=
10
69
+
10
69
=
20
69

9. The table above
shows the number of
pupils in each age group
in a class. What is the
probability that a pupil
chosen at random is at
least 11 years old
JAMB 2007
Solution
The word “at least 11” means including age 11
and above .
Total number of pupil = 40
Those pupil from at least 11 years = 27 +7 =
34
Probability that a pupil chosen at random is at
least 11=
34
40
=
17
20
Age in years 10 11 12
𝑁𝑜. 𝑜𝑓 𝑝𝑢𝑝𝑖𝑙 6 27 7

10. The table shows
classes A, B and C in a
certain school. The three
classes are put together
to select a prefect. What
is the probability that
the prefect will be a
i. a boy
ii. a girl in class B
SSCE July, 2005
Solution
Class A B C
Boys 16 13 13
Girls 14 22 18
Class A B C Total
Boys 16 13 13 42
Girls 14 22 18 54
Total 30 35 31 96
i. P(boy)=
42
96
=
7
16
ii. P(girl in B)=
22
96
=
11
48

11. 1. A normal six-sided die is thrown once. The number of outcomes in
the sample space is:
A. 1
B. 6
C. 3
D. 4
E. 5
The correct answer is 6
𝑆𝑜𝑙𝑢𝑡𝑖𝑜𝑛
The sample space,
S={1,2,3,4,5,6}
Hence the number of
outcomes is 6

12. 2. A letter is chosen randomly from the word PROBABILITY. The
probability that the letter chosen is B is:
A.
1
11
B.
2
11
C. 1
D.
2
9
E.
1
9
The correct answer is
2
11
𝑆𝑜𝑙𝑢𝑡𝑖𝑜𝑛
The number of sample space, n(s)=11
The number of Bs 𝑛 𝐵 = 2
𝑃 𝐵 =
2
11

13. 3. A ticket is selected at random from a hat containing 1 blue 2 red 1 green ticket. The
sample space is:
A. {𝑏𝑙𝑢𝑒, 𝑟𝑒𝑑, 𝑔𝑟𝑒𝑒𝑛}
B. {𝑟𝑒𝑑}
C. {𝑏𝑙𝑢𝑒, 𝑟𝑒𝑑, 𝑟𝑒𝑑, 𝑔𝑟𝑒𝑒𝑛}
D. {not red}
E. {not blue}
F. The correct answer is 𝑏𝑙𝑢𝑒, 𝑟𝑒𝑑, 𝑟𝑒𝑑, 𝑔𝑟𝑒𝑒𝑛
Solution
The sample space is 𝑏𝑙𝑢𝑒, 𝑟𝑒𝑑, 𝑟𝑒𝑑, 𝑔𝑟𝑒𝑒𝑛

14. 4. A coin is tossed once. An impossible event would be getting:
A. ℎ𝑒𝑎𝑑𝑠
B. 𝑡𝑎𝑖𝑙𝑠
C. ℎ𝑒𝑎𝑑𝑠 𝑜𝑟 𝑡𝑎𝑖𝑙𝑠
D. 𝑎 ℎ𝑒𝑎𝑑
E. 𝑎 𝑡𝑤𝑜
The correct answer is a two
Solution
A coin has only a head and a tail side. A 2 cannot show up

15. 5. The numbers 1 to 7 are written on cards, the cards are shuffled and one is selected
at random. The probability that it is a number less than 4 is:
A.
3
7
B.
4
7
C.
3
4
D.
7
3
E.
7
4
The correct answer is
3
7
Solution
The sample space,
𝑆 = {1,2,3,4,5,6,7}
𝑛 𝑆 = 7
The numbers less than 4 are {1,2,3}
𝑃 𝑡ℎ𝑎𝑡 𝑛𝑢𝑚𝑏𝑒𝑟 𝑖𝑠 𝑙𝑒𝑠𝑠 𝑡ℎ𝑎𝑛 4 =
3
7

16. 6. A bag contains 4 oranges, 3 apples and 2 bananas. If one piece of fruit is chosen at
random from the bag, find the probability that it is an apple.
A. 1
5
9
B.
1
9
C.
2
9
D.
4
9
E.
1
3
The correct answer is
1
3
𝑆𝑜𝑙𝑢𝑡𝑖𝑜𝑛
The total number of fruits = 4 + 3 + 2 = 9
𝑃 𝑎𝑝𝑝𝑙𝑒 =
3
9
=
1
3

17. 7. A bag contains 4 oranges, 3 apples and 2 bananas. If one piece of fruit is chosen at
random from the bag, find the probability that it is an apple or a banana.
A.
5
9
B.
4
9
C.
1
9
D.
7
9
E.
8
9
The correct answer is
5
9
𝑆𝑜𝑙𝑢𝑡𝑖𝑜𝑛
The total number of fruits = 4 + 3 + 2 = 9
𝑃 𝑜𝑟𝑎𝑛𝑔𝑒 =
4
9
𝑃 𝑎𝑝𝑝𝑙𝑒 =
3
9
𝑃 𝑏𝑎𝑛𝑎𝑛𝑎 =
2
9
𝑃 𝑎𝑝𝑝𝑙𝑒 𝑜𝑟 𝑏𝑎𝑛𝑎𝑛𝑎 =
3
9
+
2
9
=
5
9

18. 8. When two coins are tossed the possible outcomes are exactly 2 heads, exactly 1
head or zero heads. Given that the probability of zero heads is
1
4
qnd the probability of
exactly 1 head is
1
2
, calculate the probability of getting exactly 2 heads.
A.
1
2
B.
1
3
C.
1
4
D.
1
5
E.
3
4
The correct answer is
1
4
Solution
The sum of all the probabilities is 1.
𝑃 𝐸𝑥𝑎𝑐𝑡𝑙𝑦 1 ℎ𝑒𝑎𝑑 + 𝑃 𝐸𝑥𝑎𝑐𝑡𝑙𝑦 𝑧𝑒𝑟𝑜 ℎ𝑒𝑎𝑑𝑠 + 𝑃 𝐸𝑥𝑎𝑐𝑡𝑙𝑦 2 ℎ𝑒𝑎𝑑𝑠 = 1
1
2
+
1
4
+ 𝑃 𝐸𝑥𝑎𝑐𝑡𝑙𝑦 2 ℎ𝑒𝑎𝑠𝑑𝑠 = 1
𝑃 𝐸𝑥𝑎𝑐𝑡𝑙𝑦 2 ℎ𝑒𝑎𝑠𝑑𝑠 = 1 −
1
2
+
1
4
=
1
4

19. 9. The numbers 0 to 7 are written on cards, the cards are shuffled and one is
selected at random. What is the probability that the number is an eve number?
A.
1
2
B.
1
3
C.
3
8
D.
5
8
E.
7
8
The correct answer is
3
8
Solution
The sample space,
𝑆 = {0,1,2,3,4,5,6,7}
𝑛 𝑆 = 8
The even numbers are {0,2,4,6}
𝑃 𝑡ℎ𝑎𝑡 𝑛𝑢𝑚𝑏𝑒𝑟 𝑖𝑠 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 4 =
4
8
=
1
2

20. 10. The numbers 0 to 7 are written on cards, the cards are shuffled and
one is selected at random. What is the probability that the number is
greater than 4?
A.
1
2
B.
1
4
C.
1
8
D.
3
8
E.
3
7
Solution
The sample space,
𝑆 = {0,1,2,3,4,5,6,7}
𝑛 𝑆 = 8
The numbers greater than 4 are {5,6,7}
𝑃 𝑡ℎ𝑎𝑡 𝑛𝑢𝑚𝑏𝑒𝑟 𝑖𝑠 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 4 =
3
8

21. Summary
1. For any event A, 0 ≤ 𝑃(𝐴) ≤ 1
2. 𝑃 ∅ = 0
3. 𝑃 𝑆 = 1
4. The sum of all probabilities of events in the sample space
equals 1
5. 𝑃(𝐴 𝑎𝑛𝑑 𝐵) = 𝑃(𝐴) × 𝑃(𝐵)
6. 𝑃(𝐴 𝑜𝑟 𝐵) = 𝑃 𝐴 + 𝑃(𝐵) for mutually exclusive events
7. 𝑃(𝐴 𝑜𝑟 𝐵) = 𝑃 𝐴 + 𝑃 𝐵 − 𝑃(𝐴 ∩ 𝐵) for mutually inclusive