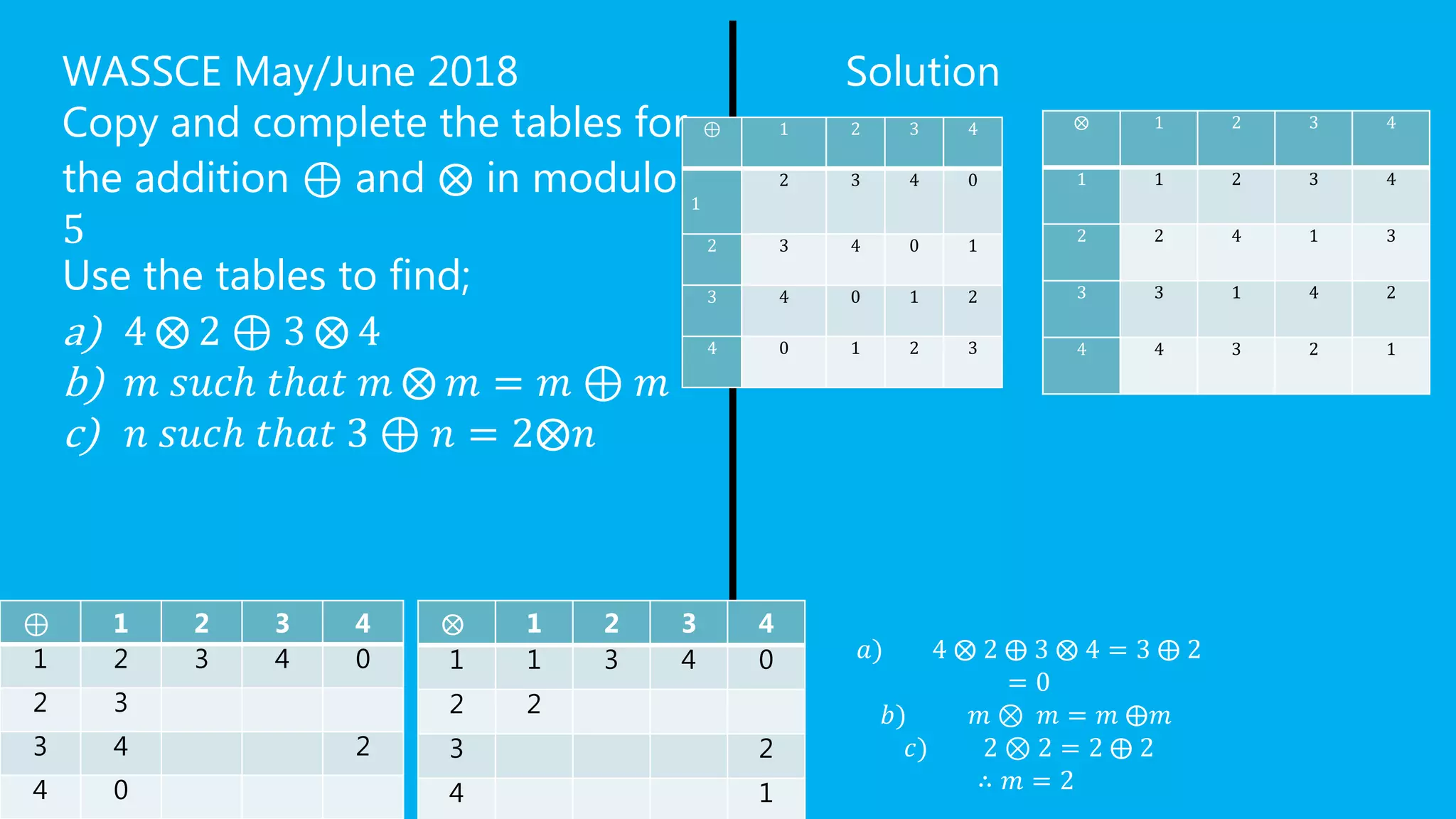
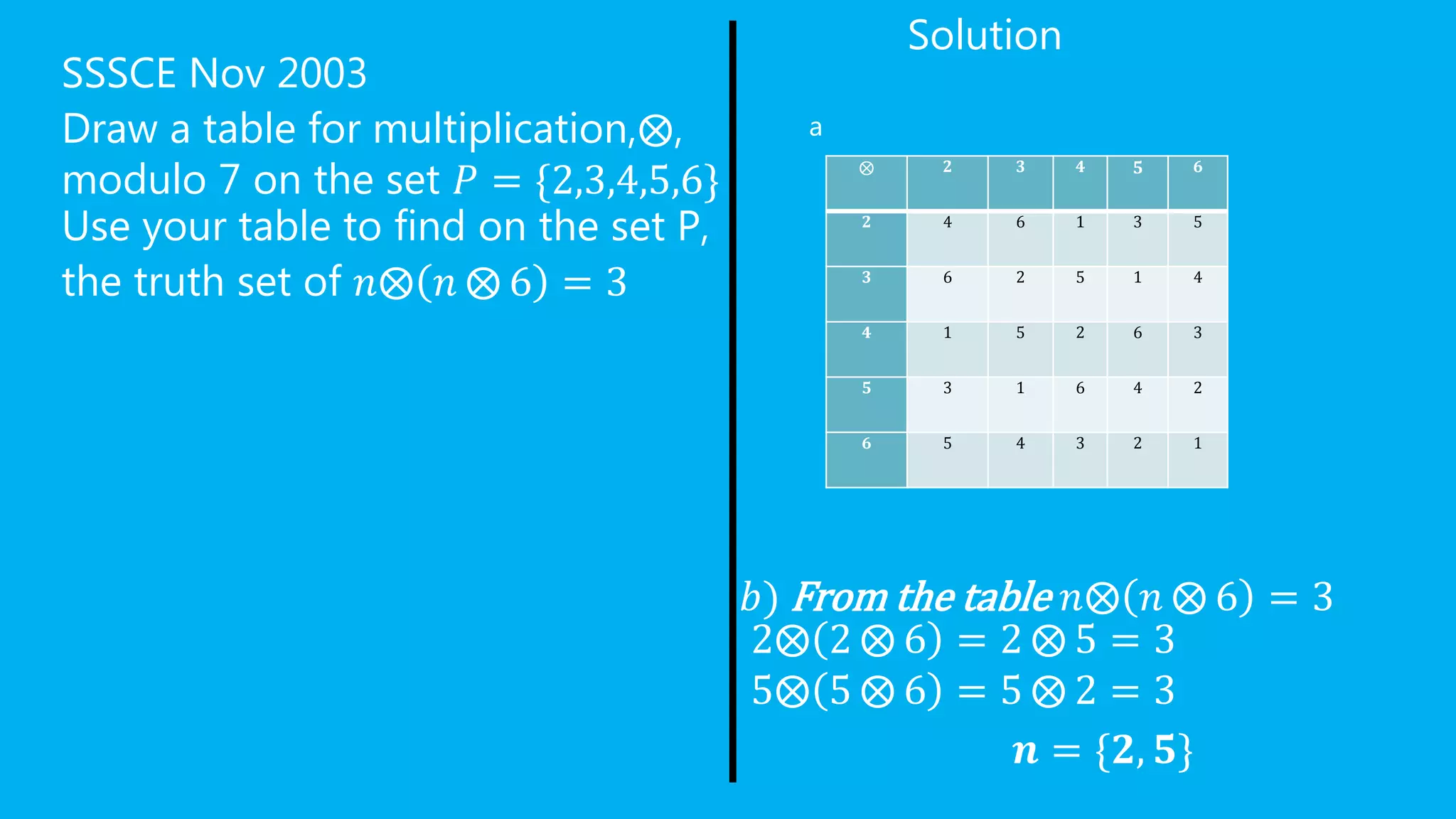
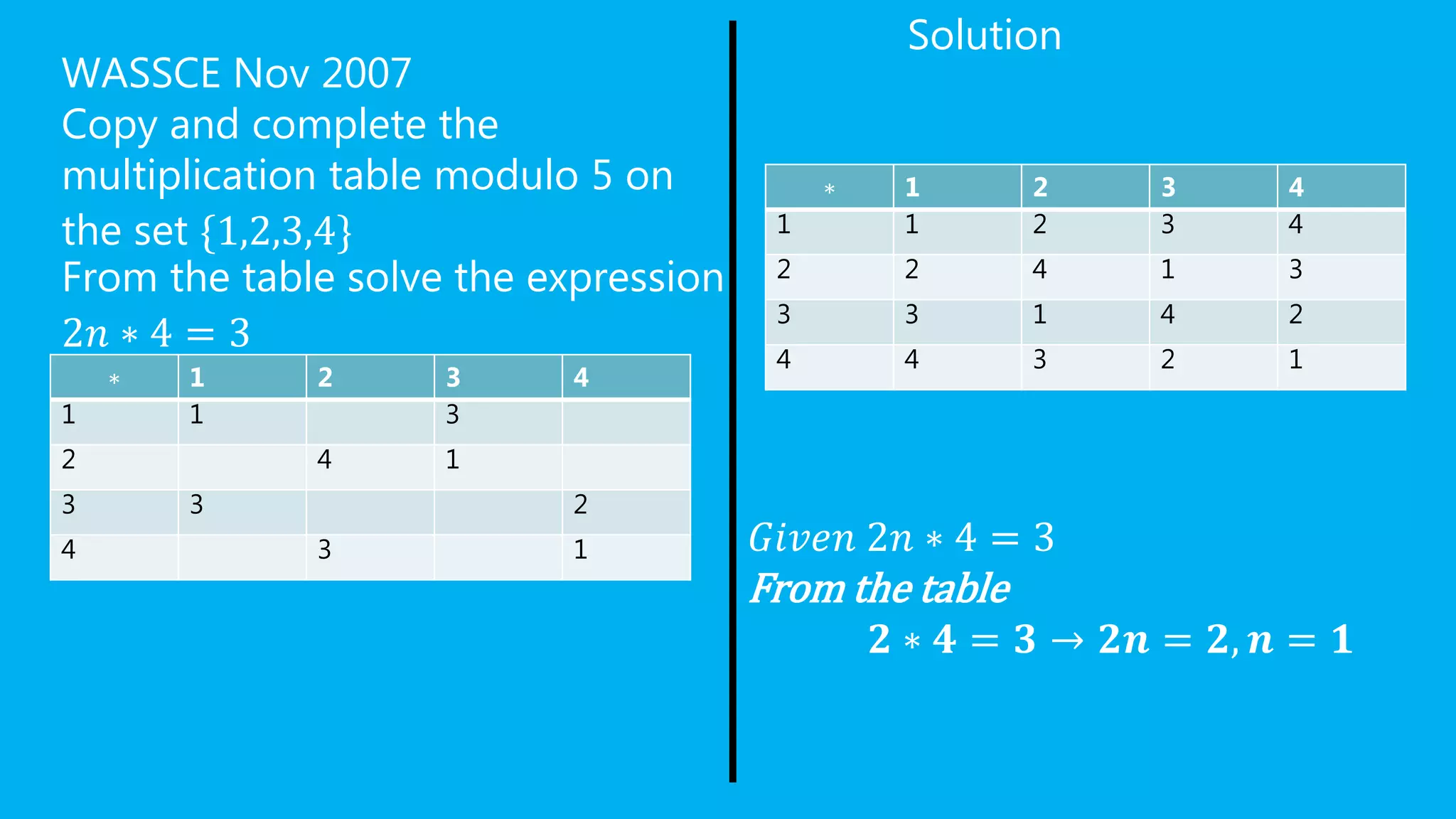
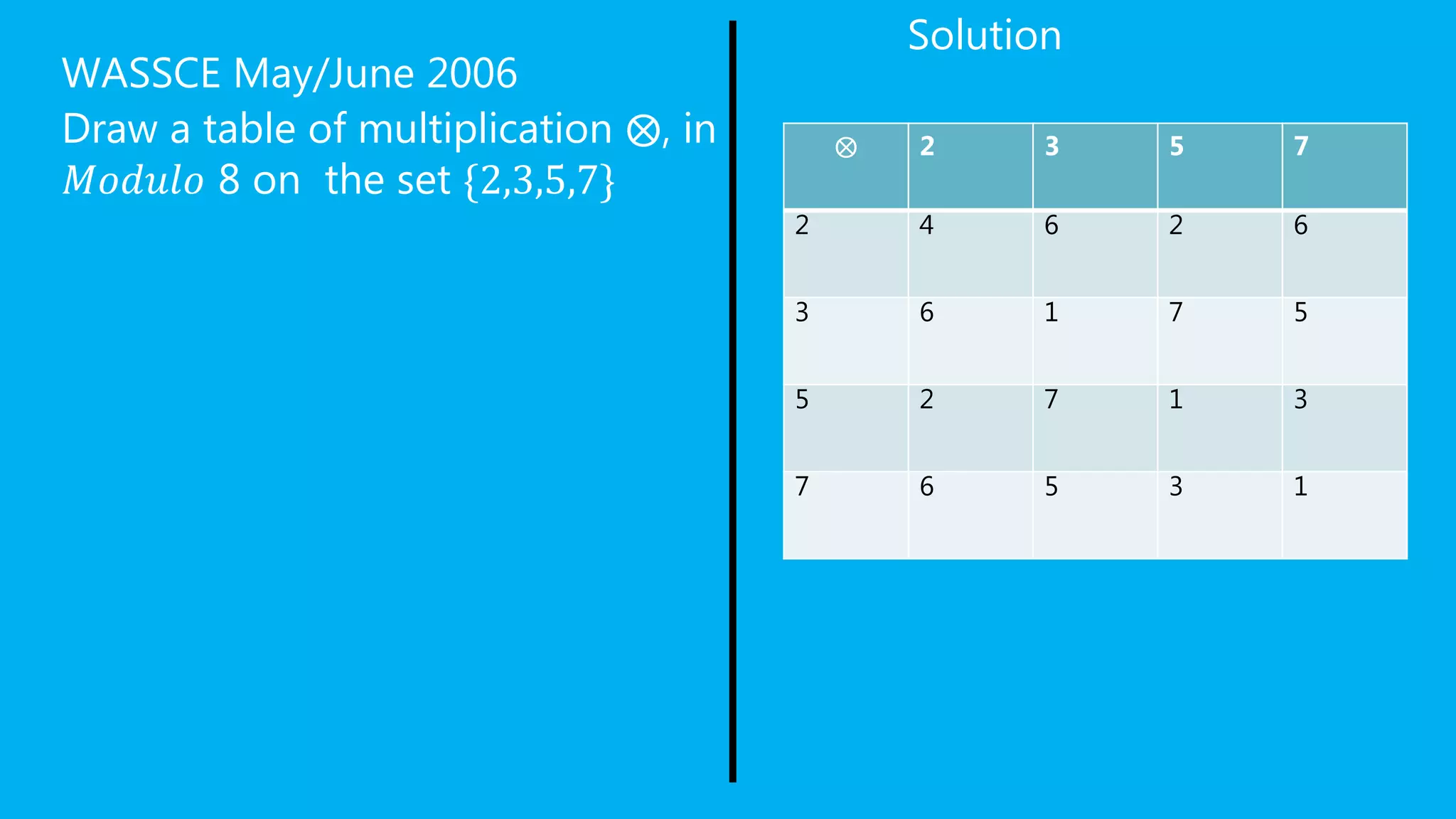
Modular arithmetic involves finding the remainder when one number is divided by another. It deals with operations like addition, subtraction, and multiplication performed on numbers modulo a given value. Some key points about modulo are that it always yields a non-negative remainder and can be used to solve congruences and expressions involving remainders of division.

1. Modular Arithmetic
Modulo is all about finding the
remainder when one number
divides another

2. WASSCE May/June 2018
Copy and complete the tables for
the addition ⊕ and ⨂ in modulo
5
Use the tables to find;
a) 4 ⨂ 2 ⊕ 3 ⨂ 4
b) 𝑚 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡 𝑚 ⨂ 𝑚 = 𝑚 ⊕ 𝑚
c) 𝑛 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡 3 ⊕ 𝑛 = 2⨂𝑛
Solution
𝑎) 4 ⨂ 2 ⨁ 3 ⨂ 4 = 3 ⨁ 2
= 0
𝑏) 𝑚 ⊗ 𝑚 = 𝑚 ⨁𝑚
𝑐) 2 ⊗ 2 = 2 ⨁ 2
∴ 𝑚 = 2
⊕ 1 2 3 4
1 2 3 4 0
2 3
3 4 2
4 0
⨂ 1 2 3 4
1 1 3 4 0
2 2
3 2
4 1
⨂ 1 2 3 4
1 1 2 3 4
2 2 4 1 3
3 3 1 4 2
4 4 3 2 1
⊕ 1 2 3 4
1
2 3 4 0
2 3 4 0 1
3 4 0 1 2
4 0 1 2 3

3. SSSCE Nov 2003
Draw a table for multiplication,⨂,
modulo 7 on the set 𝑃 = {2,3,4,5,6}
Use your table to find on the set P,
the truth set of 𝑛⨂ 𝑛 ⨂ 6 = 3
Solution
𝑏) From the table 𝑛⨂ 𝑛 ⨂ 6 = 3
2⨂ 2 ⨂ 6 = 2 ⨂ 5 = 3
5⨂ 5 ⨂ 6 = 5 ⨂ 2 = 3
𝒏 = {𝟐, 𝟓}
⨂ 𝟐 𝟑 𝟒 𝟓 𝟔
𝟐 4 6 1 3 5
𝟑 6 2 5 1 4
𝟒 1 5 2 6 3
𝟓 3 1 6 4 2
𝟔 5 4 3 2 1
a

4. WASSCE Nov 2007
Copy and complete the
multiplication table modulo 5 on
the set {1,2,3,4}
From the table solve the expression
2𝑛 ∗ 4 = 3
Solution
𝐺𝑖𝑣𝑒𝑛 2𝑛 ∗ 4 = 3
From the table
𝟐 ∗ 𝟒 = 𝟑 → 𝟐𝒏 = 𝟐, 𝒏 = 𝟏
∗ 1 2 3 4
1 1 3
2 4 1
3 3 2
4 3 1
∗ 1 2 3 4
1 1 2 3 4
2 2 4 1 3
3 3 1 4 2
4 4 3 2 1

5. WASSCE May/June 2006
Draw a table of multiplication ⨂, in
𝑀𝑜𝑑𝑢𝑙𝑜 8 on the set {2,3,5,7}
Solution
⨂ 2 3 5 7
2 4 6 2 6
3 6 1 7 5
5 2 7 1 3
7 6 5 3 1

6. 1. Simplify 9𝑚𝑜𝑑6
A. 3
B. 2
C. 1
D. 0
E. 5
F. The correct answer is 3
𝑆𝑜𝑙𝑢𝑡𝑖𝑜𝑛
9𝑚𝑜𝑑6
6 goes into 9 once
remainder 3

7. 2. Evaluate 2⨂4 in modulo 5
A. 3
B. 4
C. 2
D. 6
E. 7
The correct answer is 3
Solution
2 ⨂ 4 = 8
8𝑚𝑜𝑑5 = 3

8. 3. Given that 𝑛 ⊕ 5 = 0𝑚𝑜𝑑6. Find the value of 𝑛, such that 0 < 𝑛 < 15 .
A. 𝑛 = {1,7}
B. 𝑛 = {1,7,12}
C. 𝑛 = {0,6,12}
D. 𝑛 = {1,7,13}
E. 𝑛 = {1,13}
The correct answer is 𝑛 = {1,7,13}
Solution
𝑛 ⊕ 5 = 0𝑚𝑜𝑑6
1 ⊕ 5 = 0𝑚𝑜𝑑6
7 ⊕ 5 = 0𝑚𝑜𝑑6
13 ⊕ 5 = 0𝑚𝑜𝑑6
19 ⊕ 5 = 0𝑚𝑜𝑑6
Etc,
For 0 < 𝑛 < 15
𝑛 = {1,7,13}

9. 4. Which of the following satisfies the equation 𝑦 𝑚𝑜𝑑 7 = 1 in the
interval 0 < 𝑦 < 10?
A. {1,9}
B. {1,5}
C. {1}
D. {8}
E. {2,8}
F. {1,8}
The correct answer is
1
2
𝑝𝑞
Solution
1 𝑚𝑜𝑑 7 = 1
8 𝑚𝑜𝑑 7 = 1
𝑇ℎ𝑒 𝑣𝑎𝑙𝑢𝑒𝑠 𝑎𝑟𝑒
{1,8}

10. 5. Solve 𝑥 + 1 𝑚𝑜𝑑 5 = 3 in the interval 0 < 𝑥 < 10.
A. 𝑥 = {7,8}
B. 𝑥 = {2,8}
C. 𝑥 = {7}
D. 𝑥 = {2}
E. 𝑥 = {2,7}
The correct answer is𝑥 = {2,7}
Solution
3 𝑚𝑜𝑑 5 = 3
𝑥 + 1 = 3
𝑥 = 2
8 𝑚𝑜𝑑 5 = 3
𝑥 + 1 = 8
𝑥 = 7
13 𝑚𝑜𝑑 5 = 3
𝑥 + 1 = 13
𝑥 = 12
For the given interval
0 < 𝑥 < 10
𝑥 = {2,7}

11. 6. Find the remainder when 1001 is divided by 3
A. 2
B. 3
C. 4
D. 6
E. 5
The correct answer is 2
Solution
1001 = 3 × 999 + 2

12. 7. Evaluate 2018 𝑚𝑜𝑑 11
A. 1
B. 2
C. 3
D. 4
E. 5
The correct answer is 5
Solution
2018 = 11 × 183 + 5
2018 𝑚𝑜𝑑 11 = 5

13. 8. Find the remainder when −12 is divided by 5.
A. −3
B. 3
C. −7
D. −2
E. 5
The correct answer is 3
Solution
−12 = −5 × 3 + 3
−12 𝑚𝑜𝑑 5 = 3

14. 9. Find the remainder when −12 is divided by 3
A. −2
B. −1
C. 0
D. 1
E. 2
The correct answer is 0
Solution
−12 = −4 × 3 + 0
−12 𝑚𝑜𝑑 3 = 0

15. 10. Simplify 1 + 8𝑚𝑜𝑑6
A. 3
B. 2
C. 1
D. 0
E. 4
The correct answer is 3
Solution
1 + 8𝑚𝑜𝑑6 = 1 + 2𝑚𝑜𝑑6 = 3𝑚𝑜𝑑6

16. SUMMARY
Modulo is just about remainder
Note that remainder is not negative