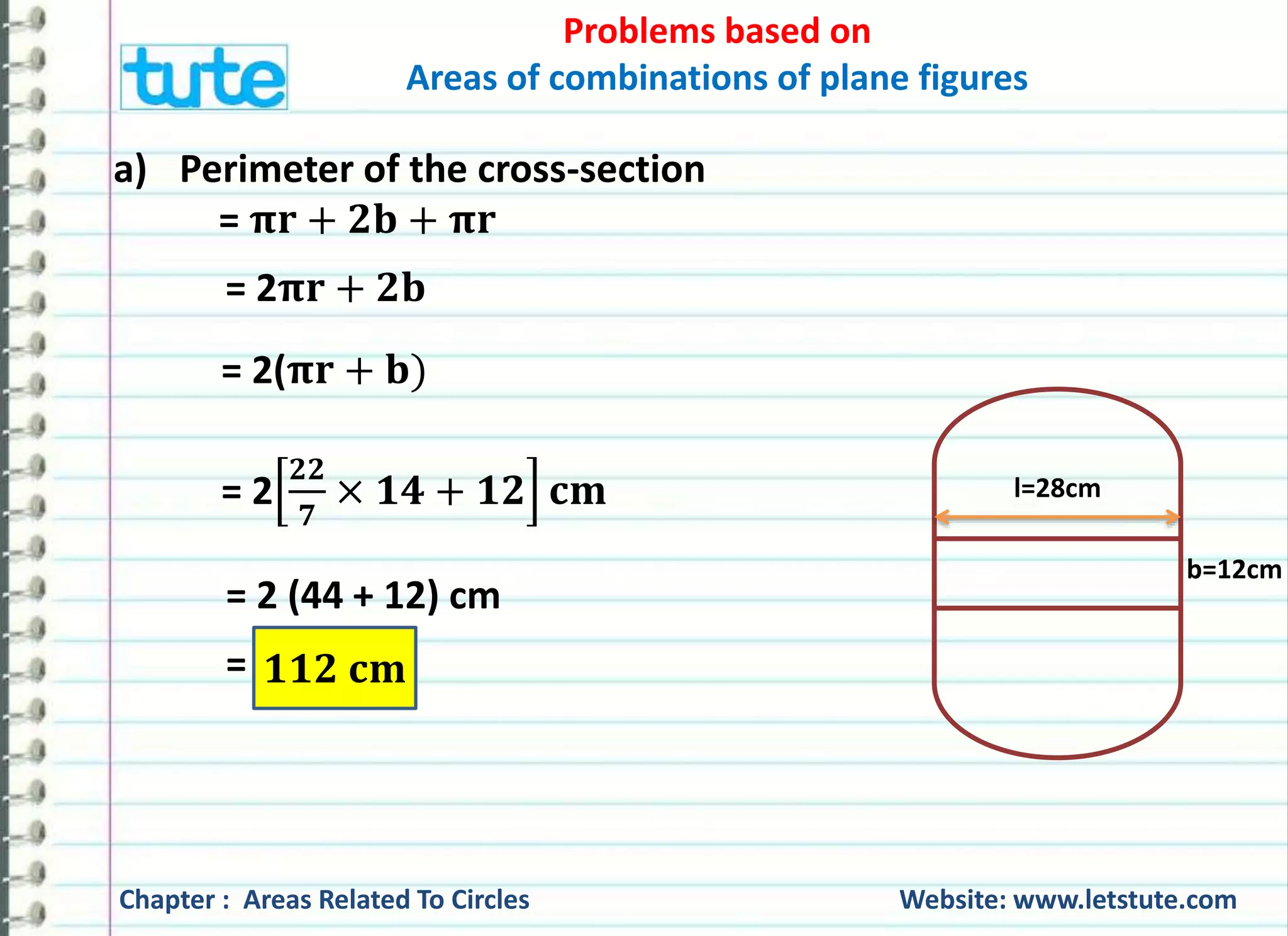
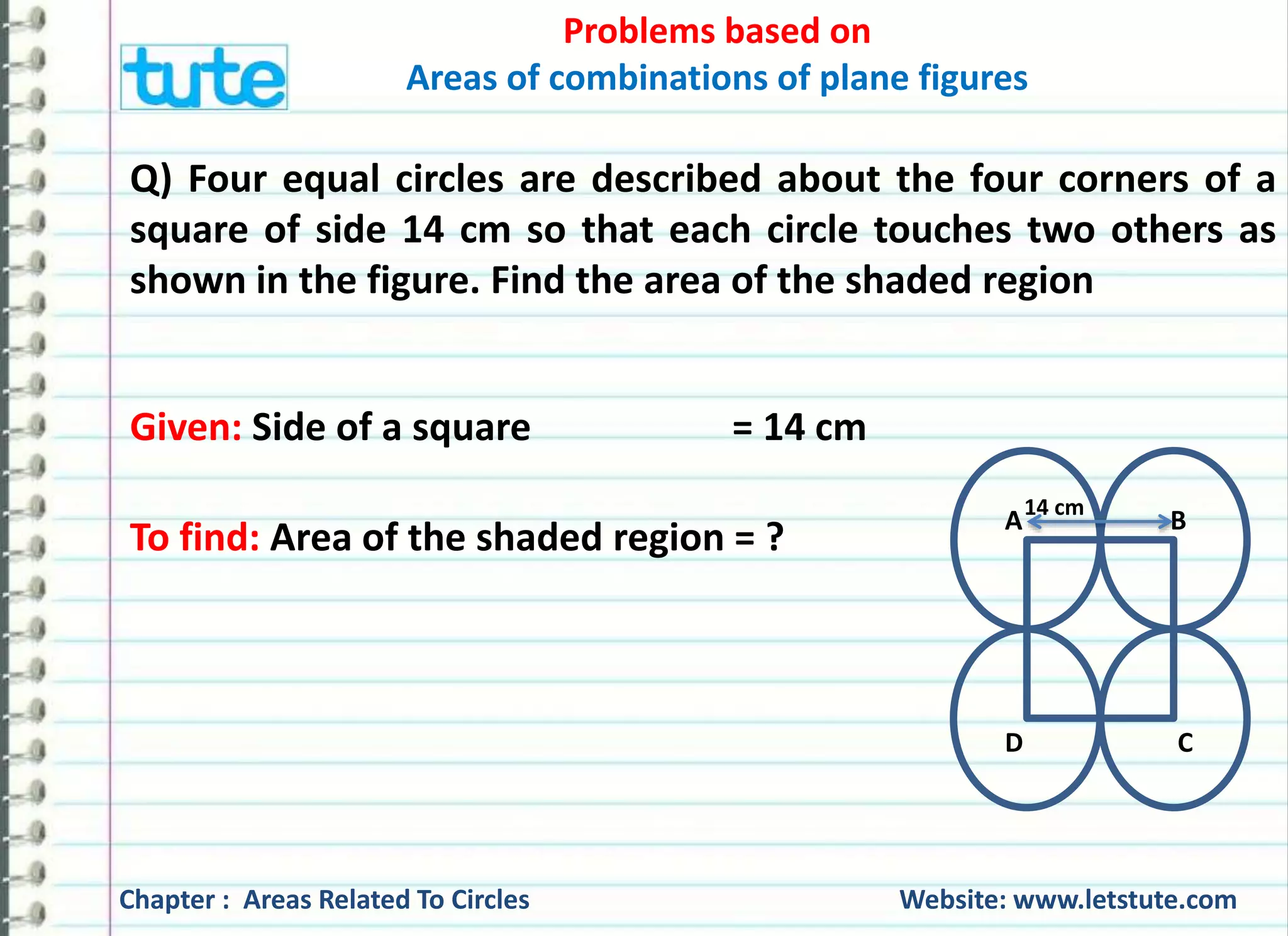
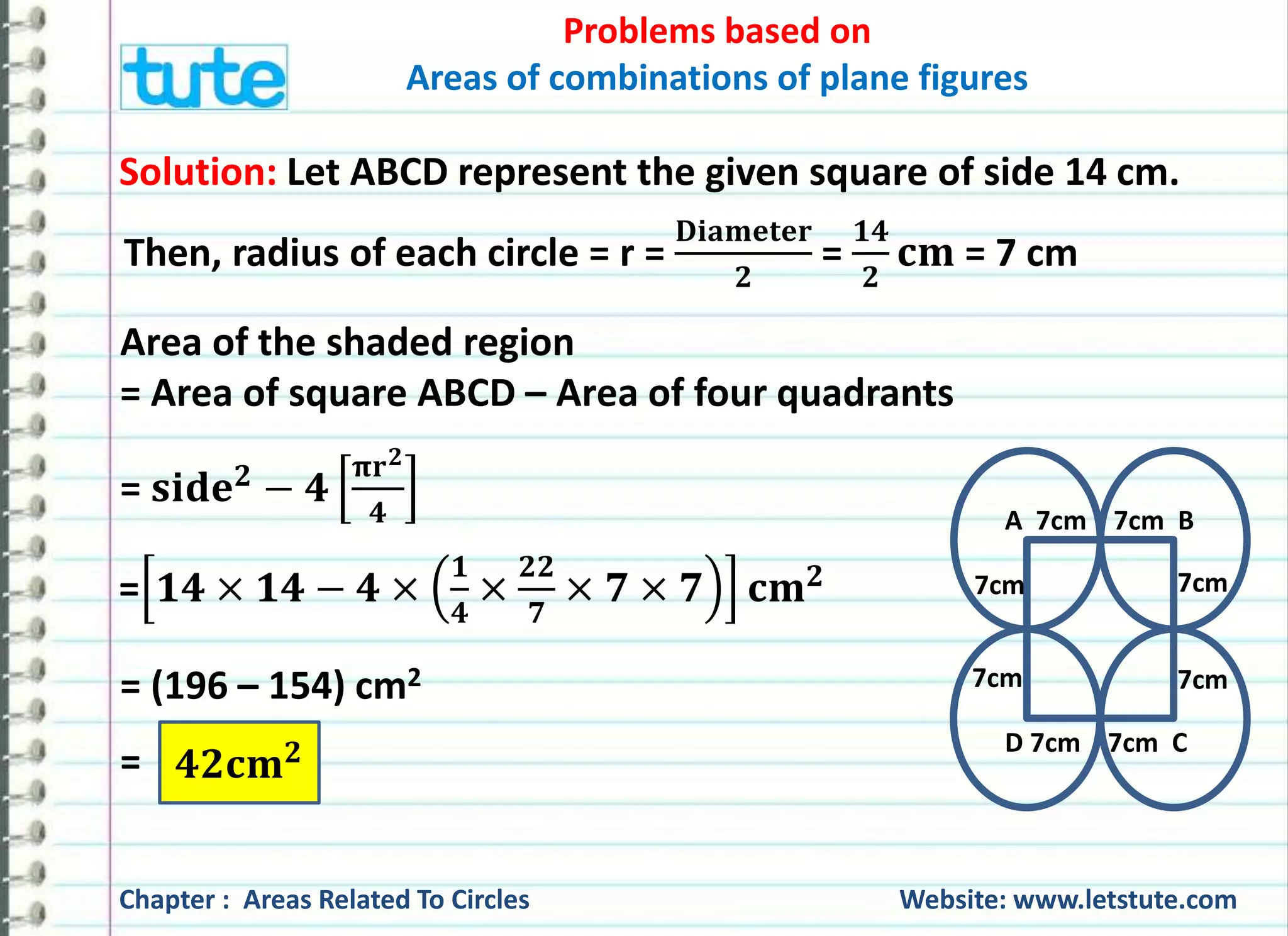
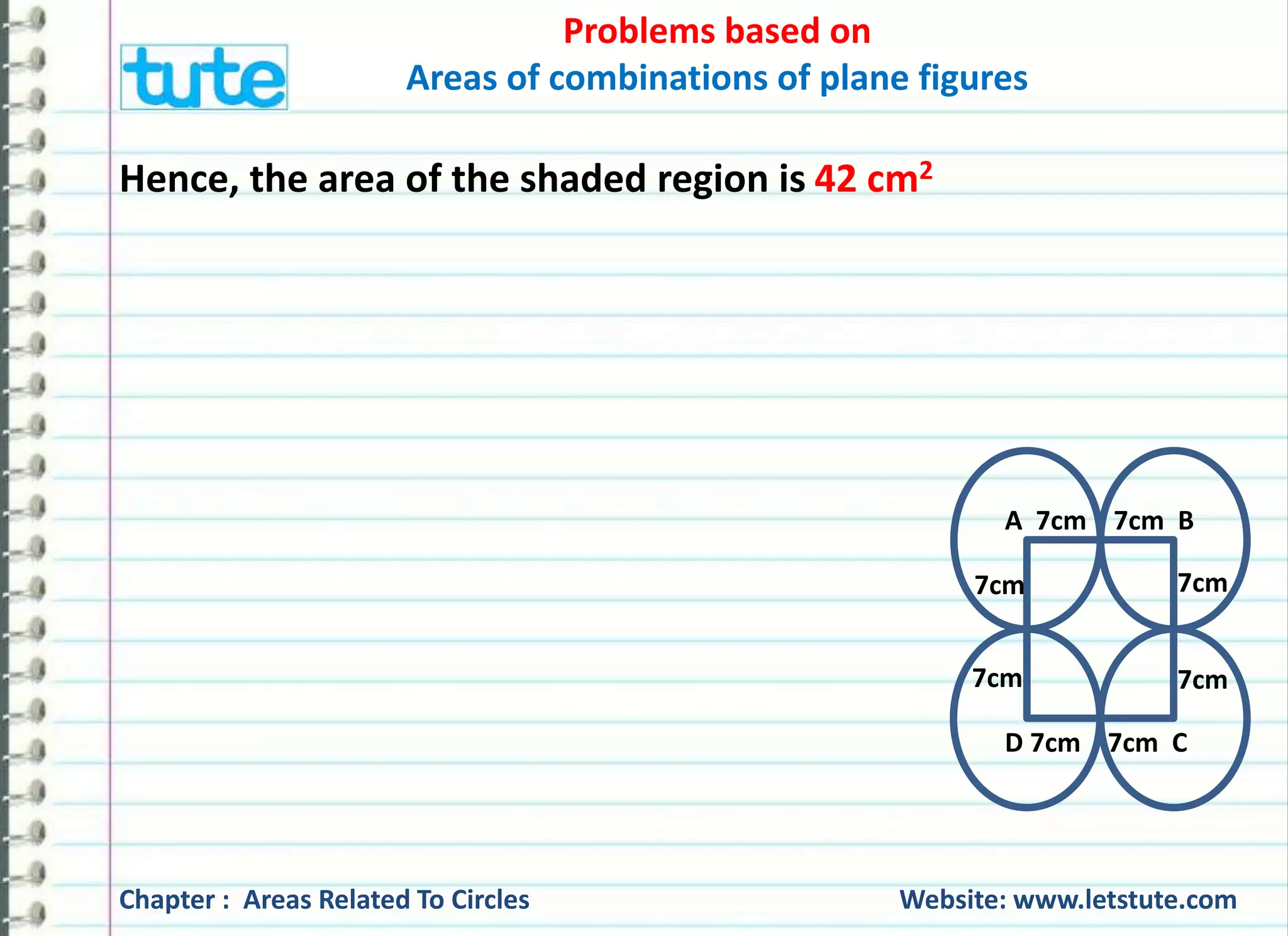
The document discusses various problems related to calculating areas and combinations of plane figures, particularly circles and squares. It provides solutions to specific problems such as finding the remaining area of a square after cutting out circles and quadrants, as well as determining the area of shaded regions in geometric figures. Additionally, it outlines the formulas used for calculating area and perimeter for different shapes.

1. Areas Related To Circles
Problems based on
Areas of combinations of plane figures
Chapter : Areas Related To Circles Website: www.letstute.com

2. Problems based on
Areas of combinations of plane figures
Q) From each corner of a square of side 8 cm a quadrant of a
circle of radius 1 cm is cut and also a circle of diameter 2 cm is
cut as shown in the figure. Find the area of the remaining
portion of the square.
Given: Side of the square = 8 cm
Quadrant of radius = 1 cm
Diameter of circle = 2 cm
To Find: Area of the remaining = ?
portion of the square
Chapter : Areas Related To Circles Website: www.letstute.com

3. Problems based on
Areas of combinations of plane figures
Solution: Area of square ABCD
= (퐬퐢퐝퐞)ퟐ
= 8 x 8 cm2
= 64 cm2
Area of a quadrant of radius 1 cm
=
=
훑퐫ퟐ
ퟒ
ퟐퟐ×ퟏ×ퟏ
ퟕ×ퟒ
퐜퐦ퟐ
=
ퟐퟐ
ퟐퟖ
퐜퐦ퟐ
∵
900
3600 =
1
4
=
ퟏퟏ
ퟏퟒ
퐜퐦ퟐ
Chapter : Areas Related To Circles Website: www.letstute.com

4. Area of four quadrants of radius 1 cm
= 4 x area of 1 quadrant
= ퟒ ×
= ퟒ ×
Areas of combinations of plane figures
훑퐫ퟐ
ퟒ
ퟏퟏ
ퟏퟒ
퐜퐦ퟐ
Problems based on
= ퟐ ×
ퟏퟏ
ퟕ
퐜퐦ퟐ
=
ퟐퟐ
ퟕ
퐜퐦ퟐ
Chapter : Areas Related To Circles Website: www.letstute.com

5. Problems based on
Areas of combinations of plane figures
Area of circle of diameter 2 cm
= 훑퐫ퟐ
=
ퟐퟐ
ퟕ
× ퟏ × ퟏ 퐜퐦ퟐ
=
ퟐퟐ
ퟕ
퐜퐦ퟐ
[∵ d = 2 cm, r = 1 cm]
Chapter : Areas Related To Circles Website: www.letstute.com

6. Problems based on
Areas of combinations of plane figures
Area of the remaining portion of square ABCD
=
퐀퐫퐞퐚 퐨퐟 퐬퐪퐮퐚퐫퐞
퐀퐁퐂퐃
−
퐀퐫퐞퐚 퐨퐟 퐟퐨퐮퐫
퐪퐮퐚퐝퐫퐚퐧퐭퐬
퐨퐟 퐫퐚퐝퐢퐮퐬 ퟏ 퐜퐦
−
퐀퐫퐞퐚 퐨퐟 퐜퐢퐫퐜퐥퐞
퐨퐟 퐝퐢퐚퐦퐞퐭퐞퐫
ퟐ 퐜퐦
= ퟔퟒ −
ퟐퟐ
ퟕ
−
ퟐퟐ
ퟕ
퐜퐦ퟐ
=
ퟒퟒퟖ − ퟐퟐ − ퟐퟐ
ퟕ
퐜퐦ퟐ
=
ퟒퟒퟖ − ퟒퟒ
ퟕ
퐜퐦ퟐ
Chapter : Areas Related To Circles Website: www.letstute.com

7. =
ퟒퟎퟒ
ퟕ
퐜퐦ퟐ
=
Areas of combinations of plane figures
ퟓퟕ. ퟕퟏퟒ 퐜퐦ퟐ
Problems based on
Hence, the area of the remaining portion of the square
is 57.714 cm2
Chapter : Areas Related To Circles Website: www.letstute.com

8. Problems based on
Areas of combinations of plane figures
Q) Four equal circles are described about the four corners of a
square of side 14 cm so that each circle touches two others as
shown in the figure. Find the area of the shaded region
Given: Side of a square = 14 cm
To find: Area of the shaded region = ?
14 cm
A B
D C
Chapter : Areas Related To Circles Website: www.letstute.com

9. Problems based on
Areas of combinations of plane figures
Solution: Let ABCD represent the given square of side 14 cm.
퐃퐢퐚퐦퐞퐭퐞퐫
Then, radius of each circle = r =
ퟐ
=
ퟏퟒ
ퟐ
퐜퐦 = 7 cm
Area of the shaded region
= Area of square ABCD – Area of four quadrants
= 퐬퐢퐝퐞ퟐ − ퟒ
훑퐫ퟐ
ퟒ
= ퟏퟒ × ퟏퟒ − ퟒ ×
ퟏ
ퟒ
×
ퟐퟐ
ퟕ
× ퟕ × ퟕ 퐜퐦ퟐ
A 7cm 7cm B
7cm
7cm
7cm
7cm
D 7cm 7cm C
= (196 – 154) cm2
= ퟒퟐ퐜퐦ퟐ
Chapter : Areas Related To Circles Website: www.letstute.com

10. Problems based on
Areas of combinations of plane figures
Hence, the area of the shaded region is 42 cm2
A 7cm 7cm B
7cm
7cm
7cm
7cm
D 7cm 7cm C
Chapter : Areas Related To Circles Website: www.letstute.com

11. Problems based on
Areas of combinations of plane figures
Q) Calculate the area of the shaded part in the figure.
[Take 훑 = ퟑ. ퟏퟒ]
Given: AD = 7 cm
DC = 24 cm
∠ADC = ퟗퟎퟎ
To find: Area of the shaded part = ?
A B
7 cm
D C
24 cm
Chapter : Areas Related To Circles Website: www.letstute.com

12. Problems based on
Areas of combinations of plane figures
AC2 = AD2 + DC2 [Pythagoras’ Theorem]
AC2 = (7cm)2 + (24cm)2
AC2 = (49 + 576) cm2
AC2 = 625 cm2
AC = 25 cm
A B
7 cm
D C
24 cm
Solution: ∠퐀퐃퐂 = ퟗퟎퟎ[Given]
퐀퐂 퐢퐬 퐭퐡퐞 퐝퐢퐚퐦퐞퐭퐞퐫 퐨퐟 퐭퐡퐞 퐜퐢퐫퐜퐥퐞.
In the right angled triangle ADC, we have,
Chapter : Areas Related To Circles Website: www.letstute.com

13. Problems based on
Areas of combinations of plane figures
Let r be the radius of the circle. Then, r =
퐃퐢퐚퐦퐞퐭퐞퐫
ퟐ
=
퐀퐂
ퟐ
=
ퟐퟓ
ퟐ
cm
= 12.5 cm
Area of the shaded part
= Area of the circle – Area of the rectangle
= (훑퐫ퟐ) − (퐥퐞퐧퐠퐭퐡 × 퐛퐫퐞퐚퐝퐭퐡)
= [3.14× ퟏퟐ. ퟓ)ퟐ − ퟐퟒ × ퟕ 퐜퐦ퟐ
A B
7 cm
D C
24 cm
= (3.14) × ퟏퟓퟔ. ퟐퟓ − ퟏퟔퟖ 퐜퐦ퟐ
Chapter : Areas Related To Circles Website: www.letstute.com

14. Areas of combinations of plane figures
= (490.625 – 168)퐜퐦ퟐ
= ퟑퟐퟐ. ퟔퟐퟓ퐜퐦ퟐ
Problems based on
Hence, the area of the shaded part is 322.625 cm2
A B
7 cm
D C
24 cm
Chapter : Areas Related To Circles Website: www.letstute.com

15. Problems based on
Areas of combinations of plane figures
Q) The given figure is a cross section which consists of a rectangle
and two semi circles. From the information given, find
a) Perimeter of the cross-section
b) Area of the cross-section.
Given: Length of the rectangle = 28cm
Breadth of the rectangle = 12cm
To find: a) Perimeter of the cross-section
b) Area of the cross-section.
l=28cm
b=12cm
Chapter : Areas Related To Circles Website: www.letstute.com

16. Problems based on
Areas of combinations of plane figures
Solution: Let the length and breadth of the rectangle be l and b
respectively,
Let r be the radius of each semicircular part of the cross-section.
Then, l = 28 cm, b = 12 cm
And r =
퐃퐢퐚퐦퐞퐭퐞퐫
ퟐ
=
ퟐퟖ
ퟐ
cm = 14 cm
l=28cm
b=12cm
Chapter : Areas Related To Circles Website: www.letstute.com

17. Problems based on
Areas of combinations of plane figures
a) Perimeter of the cross-section
= 훑퐫 + ퟐ퐛 + 훑퐫
= 2훑퐫 + ퟐ퐛
= 2(훑퐫 + 퐛)
= 2
ퟐퟐ
ퟕ
× ퟏퟒ + ퟏퟐ 퐜퐦
= 2 (44 + 12) cm
= ퟏퟏퟐ 퐜퐦
l=28cm
b=12cm
Chapter : Areas Related To Circles Website: www.letstute.com

18. Problems based on
Areas of combinations of plane figures
b) Area of the cross-section
= Area of the 2 semicircles + area of the rectangle
= 2
훑퐫ퟐ
ퟐ
+ 퐥퐛
= 훑퐫ퟐ + 퐥퐛
=
ퟐퟐ
ퟕ
× ퟏퟒ × ퟏퟒ + ퟐퟖ × ퟏퟐ cm2
= 616 + 336 퐜퐦ퟐ
= ퟗퟓퟐ 퐜퐦ퟐ
l=28cm
b=12cm
Chapter : Areas Related To Circles Website: www.letstute.com

19. Problems based on
Areas of combinations of plane figures
Hence, a) The perimeter of the cross-section is 112 cm
b) The area of the cross-section isퟗퟓퟐ 퐜퐦ퟐ
l=28cm
b=12cm
Chapter : Areas Related To Circles Website: www.letstute.com

20. Now we know…
Problems based on
Areas of combinations of plane figures
Please visit www.letstute.com to take a test
Chapter : Areas Related To Circles Website: www.letstute.com

21. Next video….
Problems based on Area Related to Circles
Higher Order Thinking Skills (HOTS)
Please visit www.letstute.com to view the next video
Chapter : Areas Related To Circles Website: www.letstute.com